具有树和路约束的平行机排序问题*

程佳乐，李伟东

(云南大学数学与统计学院，云南昆明650504)

1 引言

以最小化最大机器负载为目标的平行机排序问题在网络资源分配、工业工程和电信等领域被广泛应用，是运筹学和理论计算机科学等领域研究的重点内容之一。由于科学与社会的迅速发展，给制造、服务和管理等不同领域带来了许多新问题，单纯的平行机排序问题已不适用于实际情况。对此，Wang等人［1］首次提出具有图结构约束的平行机排序问题。本文主要考虑具有树和路约束的平行机排序问题，其定义如下:给定一无向图(有向图)，机器集 M={1，…，m}和工件集J={1，…，n}，任务j的处理时间为pj，工件集与无向图(有向图)的边(弧)一一对应。选定一工件子集分配到m台机器上处理，每个工件只能分配一台机器。

令Sl表示在机器l上处理的工件集，机器l上的负载定义为在其上加工的所有工件的权重之和。本文要求寻找一种分配方案使得被选中的工件子集满足无向图(有向图)上的路或树的约束，目标是机器的最大负载(记为Cmax)尽可能达到最小。

为更好地陈述相关的研究成果，下面给出理论计算机科学领域内与本文相关的基本定义。

定义1［2］令Π 表示一个最小化问题，I是该问题的任意一个实例，A表示问题Π的一个多项式时间算法，A(I)和OPT(I)分别表示算法A解决实例I所得到的可行解的目标函数值和最优值，则算法A的近似比定义为:

定义2［2］对于最小化问题Π，若对任意的实数ε＞0，算法簇Aε都有一个(1+ε)-近似解，且运行时间是关于输入长度的多项式函数，则称算法簇Aε是一个多项式时间近似方案PTAS(Polynomial Time Approximation Scheme)。如果算法簇Aε的运行时间为，则称之为有效多项式时间近似方案EPTAS(Efficient Polynomial-Time Approximation Scheme)，其中，f(1/ε) 表示关于1/ε的函数表示关于输入长度的多项式函数。

Wang等人［1］于2012年首次提出具有顶点覆盖约束的平行机排序问题(简记为P|vertex cover|Cmax)，其中，P表示在平行机器的环境下加工，Cmax表示机器的最大负载。对给定无向图G=(V，E;w)，w:V→Q+(V、E分别是图G的顶点集合和边集合，w是对顶点集V的赋权)，要找一顶点子集V'V，使得图上每条边至少有一个顶点属于集合V'，则称此顶点子集V'是一个顶点覆盖。作者研究了在m台相同的平行机上调度一组加权顶点子集，使得该子集是一个顶点覆盖，目标是使得机器的最大完工时间最小化。基于局部比率法和LPT(Largest Processing Time)算法，提出了近似比为3的算法。随后，Wang等人［3］给出具有覆盖约束的同类机排序问题的通用性算法，算法的近似比依赖于覆盖问题的难度。2016年，Epstein等人［4］提出了关于Pm|vertex cover|Cmax问题(机器数m固定)的2-近似算法以及关于P|vertex cover|Cmax问题(机器数m不固定)的(2+ε)-近似算法(ε＞0为任意常数)。

与此同时，Nip 等人［5，6］研究在最短路约束下的流水车间调度问题，即选取工件集的一个子集使其是给定图中的一条路，将该工件子集中的工件放在流水车间处理，目标是使其最大完工时间(makespan)尽可能小。对于具有最短路约束的流水车间调度问题，当机器数为2时(简记为F2|shortest path|Cmax)，分别存在近似比为 2和(3/2)(1+ε) 的算法。随后，Nip 等人［7］研究在最短路约束下的开放车间调度(Open Shop Scheduling)和作业车间调度(Job Shop Scheduling)问题(简记为 Om|shortest path|Cmax，Jm|shortest path|Cmax)，即选取工件集的一个子集使其是给定图中的一条路，将该工件子集中的工件放在开放车间或作业车间条件下处理，目标是使得最大完工时间(makespan)尽可能小。

集装箱问题和图结构约束组合的问题也受到研究人员的关注。Li等人［8］研究了一系列具有图结构约束的特殊材料的构建问题，作者于2014年首先考虑以下问题:给定一有向图D=(V，A;w)以及长度为L的特定材料，要求在D中构造一个具有特殊结构的子图D'，使得D'中的每一条弧都由特定材料构成，目标是使得在D'中构建所有弧的材料根数尽可能少(若弧长超过L，可用多根材料“拼接”而成)。对子图D'的构建可等价于装箱问题(箱子容量为L，对被选中物品(弧)构建相应的装箱实例，目标是使得所需箱子数目最少)。随后，Li等人［9］研究了具有支撑树 CST(Constructing Spanning Tree)、单源最短路径树CSSPT(Constructing Single-source Shortest Path Tree)和满足三角不等式的Steiner树CMST(Constructing Metric Steiner Tree)等结构约束的装箱问题。对于此三类问题，，其中k表示用长度为L的材料对K-tree TK中的边集合进行构建所需要的材料根数。作者证明此问题是NP-hard的，且对于ε＞0，此问题的最优算法的近似比为3/2－ε，除非P=NP，并利用最小费用支撑K-树的相关性质可得一个2-近似算法。

受上述文献的启发，本文主要研究如下四个问题:(1)在无向图上分别具有路和K-树约束的平行机排序问题;(2)在有向图上分别具有单源点最短路径树和两点间最短路约束的平行机排序问题。

本文结构如下:第2节给出四种问题的定义;第3节描述了解决无向图上具有K-树约束的平行机排序问题的α-近似算法(若平行机排序算法Α的近似比为α)，从而可有一个EPTAS;第4节给出一个解决无向图上具有路的约束的平行机排序问题的(2－1/m)-近似算法;第5节提出解决有向图上具有单源点最短路径树约束的平行机排序问题的α-近似算法(若平行机排序算法Α的近似比为α)，从而也可以得到一个EPTAS;第6节给出一个解决有向图上两点间最短路约束的平行机排序问题的1．618-近似算法;第7节对全文进行总结，并指出未来值得研究的方向。最好的算法近似比皆为3/2－ε，除非P=NP(ε＞0)。并对于CST问题和CSSPT问题分别提出了近似比都为3/2的算法，针对CMST问题，设计了一个近似比为4的算法。最近，Lichen等人［10］研究了具有K-树约束的最小费用装箱问题。对于无向图G=(V，E;w，c)以及长度为L且费用为c0的特定材料，满足w:E→Q+，c:E→(w为长度函数，c为费用函数)，新的目标为

2 问题描述

经典的平行机排序问题定义为:给定n个互相独立的工件J={1，…，n}，m台完全相同的机器M={1，…，m}(并行运行)，每个工件只需在一台机器上不中断地加工一次，并设m ＜n;工件j的处理时间为pj，所有工件在零时刻到达且所有机器在零时刻即可加工，并要求工件一旦在某个机器上加工就必须加工完毕，不允许中断，目标是尽快加工完所有工件。如果工件j在时刻Cj被加工完成，则目标是找到一种调度使得机器的最大完工时间 Cmax尽可能地小，即 Cmax=maxj=1，…，nCj。本文主要考虑具有树或路约束的平行机排序问题，涉及的定义如下:

定义3［11］(K-树) 给定一无向图 G=(V，E;w)，|V|=n+1，K-树就是在图G中找一个连通的支撑子图TK=(V，ETK)，并且K=0时，0-树就是支撑树。

定义4(P|K-tree|Cmax) 给定无向图G=(V，E;w)，|V|=n+1，|E|条边分别为 e1，…，e|E|，w:E→Z+，K为固定正整数;m台机器，每一条边ej∈E对应一个工件j∈J，加工时间为pj=wj;要找一棵K-树TK=(V，ETK)，将其边集合ETK对应的工件集放在平行机下处理，目标是使其最大完工时间(makespan)尽可能小。

定义5(P|s-t path|Cmax) 给定无向图G=(V，E;w)，两个固定顶点 s，t∈ V，w:E → Z+，|V|个顶点分别为v1，…，v|V|，|E|条边分别为e1，…，e|E|;m台机器，每一条边ej∈E对应一个工件j∈J，加工时间为 pj=wj，要找一条 s-t路 Pst=(V(Pst)，E(Pst))，将其边集合E(Pst)对应的工件集放在平行机下处理，目标是使其最大完工时间(makespan)尽可能小。

定义6最短路径树(the shortest path tree) 给定一有向图D=(V，A;s;w)，s为固定顶点，w:A→Z+;要找一棵以s为根的最短路径树T=(V，As)，使得在T中从根s到其他任何顶点u∈V－{s}的距离是原图D上从s到u的最短路径距离。

定义7(P|the shortest path tree|Cmax) 给定一有向图 D=(V，A;s;w)，|V|=n+1，s为固定顶点，w:A→Z+;m台机器，每一条弧ej∈A对应一个工件j∈J，加工时间为pj=wj，要找一最短路径树Ts=(V，A's)，将其弧集合A's对应的工件集放在平行机下处理，目标是使其最大完工时间(makespan)尽可能小。

定义8(P|the shortest s-t path|Cmax) 给定一有向图 D=(V，A;s，t;w)，s，t为固定顶点，w:A →Z+，|V| 个顶点分别为 v1，…，v|V|，条弧分别m台机器，每一条弧ej∈A对应一个工件j∈J，加工时间为pj=wj，要找一条最短s-t路 SPst= (V(SPst)，A(SPst))，将 其 弧 集 合A(SPst)对应的工件集放在平行机下处理，目标是使其最大完工时间(makespan)尽可能小。

3 P|K-tree|Cmax问题

在本节中，考虑在K-树约束下的平行机排序问题。对于此问题，我们的策略是:(1)调用Fisher算法［11］在图 G中寻找一棵最小支撑 K-树 TK=(V，ETK);(2)将边集合ETK对应的工件集运用平行机调度算法Α进行排序。

问题P|K-tree|Cmax的近似算法描述如下:

算法1问题P|K-tree|Cmax的近似算法

Input:无向图G=(V，E;w)及非负整数K。

Output:S1，S2，…，Sm和 Cmax。

Begin

Step 1在图G中调用Fisher算法［11］寻找一棵最小支撑 K-树 TK=(V，ETK) ，其边集合 ETK={ei1，ei2，…，ein+K} ，对应工件集为 {i1，i2，…，in+K}。

Step 2应用算法Α调度工件集{i1，i2，…，in+K}。

Step 3输出 S1，S2，…，Sm和 Cmax，这里 Si表示分配给机器i的工件集。

End

要证明算法1的近似比，首先引入如下引理:

引理1给定无向图G=(V，E;w)，|V|=n+1，w:E→Z+，K 为非负整数;TK=(V，ETK)是图 G的一棵最小支撑 K-树，其边集 ETK={ei1，ei2，…，ET*K)是对应于问题P|K-tree|Cmax最优解的一棵最优支撑K-树，其边集且有…，n+K。

考虑以下两种情形，每种情形都将导致矛盾，从而证明该引理。

情形1至少存在一条边 eit'∈{eit，eit+1，…，ein+K}，使得eit'不是图G的割边。

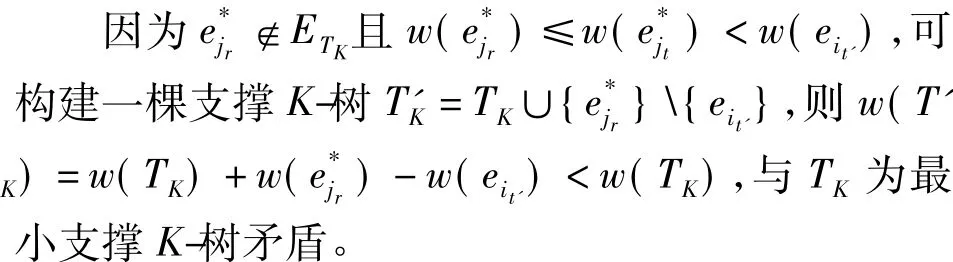
情形2每一条边都是图G的割边。

由算法1，我们得到P|K-tree|Cmax问题的以下结果:

定理1对于P|K-tree|Cmax问题，若子算法Α是α-近似，则算法1是α-近似的;且算法1的时间复杂度为O(n2+T(m，n))，其中T(m，n)是调度算法Α的运行时间。

证明设TK=(V，ETK)是由算法1得到的最小支撑 K-树，其边集合且 w，输出解为 S1，S2，…，Sm，输出值 C是对应于最优值的最优支撑K-树，其边集合

由于平行机排序问题存在EPTAS［12］，所以有:

推论1P|K-tree|Cmax问题有EPTAS。

4 P|s-t path|Cmax问题

在本节中，考虑在路的约束下的平行机排序问题。对于此问题，我们的策略是:(1)给定原图G=(V，E;s，t;w)，两个固定顶点 s，t∈ V，w:E →Z+，对图G上的每一条边ek，构建新图Gk=(V，Ek;w)(边e∈Ek当且仅当w(e)≤w(ek))，在图Gk中调用 prim's算法［13］寻找一条最短 s-t路对应的工件运用LS(List Scheduling)算法进行平行机上的排序，得到可行解及其目标函数值Ckmax;(2)比较|E|个可行解的目标函数值，取其最小值作为输出值。

问题P|s-t path|Cmax的近似算法描述如下:

算法2问题P|s-t path|Cmax的近似算法

Input:无向图 G=(V，E;s，t;w);s，t∈ V。

Output:S1，S2，…，Sm和 Cmax。

Begin

Step 1置S1=S2=… =Sm=，Cmax=+∞。

Step 3输出 S1，S2，…，Sm和 Cmax。

End

由算法2，我们得到P|s-t path|Cmax问题的以下结果:

定理2算法2是一个复杂度为O(|E|(|V|2+|E|m))的(2－1/m)-近似算法。

5 P|the shortest path tree|Cmax问题

在本节中，考虑在最短路径树的约束下的平行机排序问题。对于此问题，我们的策略是:(1)对于有向图D=(V，A;s;w)的源顶点s，使用Dijkstra算法［14］构造一个辅助无圈有向图Ds=(V，As;s);(2)对每个顶点u∈V－{s}，在Ds中选择一条进入u且其权重最小的入弧，得到以s为根的树形图Ts=(V，A's);(3)将弧集合A's对应的工件集运用平行机调度算法Α进行排序。

问题P|the shortest path tree|Cmax的近似算法描述如下:

算法3 问题P|the shortest path tree|Cmax的近似算法

Input:有向图 D=(V，A;s;w)。

Output:S1，S2，…，Sm和 Cmax。

Begin

Step 1对D中的源顶点s，使用Dijkstra算法［14］构造一辅助无圈有向图Ds=(V，As;s)。

Step 2对于每个顶点u∈V－{s}，在Ds中选择一条进入u且其权重最小的入弧，得到一个以s为根的树形图 Ts=(V，A's) ，其中 A's={ei1，…，ein} ，对应工件集为{i1，…，in}。

Step 3应用算法Α调度工件集{i1，…，in}。

Step 4输出 S1，S2，…，Sm和 Cmax。

End

由算法3，我们得到P|the shortest path tree|Cmax问题的以下结果:

定理3对于P|the shortest path tree|Cmax问题，若子算法 Α是 α-近似的，则算法3是 α-近似的;且算法3的时间复杂度为O(n2+T(m，n))，其中T(m，n)是调度算法Α的运行时间。

对于图Ts=(V，A's)和图，有s定义为进入顶点vk+1(k=1，…，n)的入弧 (在图定义为进入顶点vk+1的入弧)，因为在图 Ds= (V，As;s) 中，满足 dG(s，x) =dDs(s，x)(x∈ V) ，由 Step 2有:

(1)Ts是以s为根的最小树形图(TsDs)。

(2)dDs(s，x)=dTs(s，x)(x ∈ V)。

6 P|the shortest s-t path|Cmax问题

在本节中，考虑在最短s-t路的约束下的平行机排序问题。对于此问题，我们的策略是:(1)运用Dijkstra算法［14］求得所有最短s-t路构成的子图(其中 A'是构成所有最短 s-t路的弧集合，必有其权重值w(e)保持不变)及其最短路长度(记为L);(2)对图上的每一条边ek，构建新图，(在这里(3)在图 Dk中调用 prim’s算法［13］寻找一条权重为 w'(e)时的最短 s-t路SPk

st=(V(SPst)k，A(SPst)k) ，将 A(SPst)k对应的运用LPT算法进行平行机上的排序，得到可行解及其目标函数值个可行解的目标函数值，取其最小值作为输出值。

P|the shortest s-t path|Cmax问题的近似算法描述如下:

算法4 P|the shortest s-t path|Cmax问题的近似算法

Input:有向图 D=(V，A;s，t;w)。

Output:S1，S2，…，Sm和 Cmax。

Begin

Step 1置S1=S2=… =Sm=，Cmax=+∞。

Step 2运用Dijkstra算法［14］求得所有s-t最短路构成的子图D'=(V，A';s，t;w)及其最短路长度(记为L)。

Step 4输出 S1，S2，…，Sm和 Cmax。

End

引理2在所有可行解中，当k=τ时，大工件数目最少。

证明在图D'中，由权重w'的构造知，上的大工件数目最少。证毕。 □

引理3在可行解中，最多有2m个大工件，即对于任意的(l=1，…，m) ，加工的大工件数最多为2。

证明(反证法) 若可行解中的大工件数超过2m，则对所有工件完成时间之和T有:T，不构成s-t最短路的可行解，矛盾，从而结论成立。证毕。 □

由算法4，我们可得P|the shortest s-t path|Cmax问题的以下结果:

定理4算法4是一个复杂度为O(|V|2+的-近似算法。

情形1大工件数不超过m。

情形2大工件数超过m。

7 结束语

本文具体研究了四种在树和路约束下的平行机排序问题，设计了相应的多项式时间算法，并分析了算法的近似比。其中，在无(有)向图上具有(最短)路约束的平行机排序问题，能否设计一个更好的近似算法是值得研究的问题。

文献［3］给出了具有覆盖约束的平行机排序问题的通用算法。Wang等人［3］指出，对于特定的图结构约束，能否设计更好的近似算法值得探讨。本文中所提到的四个问题正是特定的图结构约束下的平行机排序问题，但是，还有许多图结构(如树形图等)约束的平行机排序问题的近似算法设计问题未得到解决。