局部相似性优化的p-谱聚类算法*

胡乾坤，丁世飞

中国矿业大学 计算机科学与技术学院，江苏 徐州 221116

1 引言

聚类是数据挖掘领域中热门的研究课题之一，其研究目的是根据相似性的大小把数据分到不同的簇中，使得簇内数据之间的相似性尽可能大，簇间数据之间的相似性尽可能小。目前，很多聚类算法已经被提出，例如层次聚类[1]、k-means聚类[2]、支持向量机[3]、初始化独立聚类[4]、多视图聚类[5]等算法。近几年来，谱聚类算法逐渐发展成为较重要的聚类算法之一，原因是其具有较强的概括性、有效性和丰富的理论基础[6]。谱聚类算法的理论基础包括平衡图切判据、随机游走和扰动理论[7]。谱聚类算法的核心思想是把样本空间的聚类问题转化无向图G的图划分问题。数据样本视作无向图G上的顶点，数据样本对之间的相似性视作顶点之间边的权重。一般谱聚类算法包含以下3个步骤：第一，根据所给的样本数据集，定义一个相似性矩阵来描述数据之间的相似性；第二，进一步构建拉普拉斯矩阵并计算其特征值和对应特征向量；第三，选择合适的特征向量，使用传统聚类算法对数据样本进行聚类[8]。

最近，在谱聚类中引入p-Laplacian算子，引起了研究者的广泛关注。它使得算法可以获得较好的图切判据，即Cheeger cut（Ccut或者齐格切）[9]。Ccut旨在寻求一种簇内数据样本之间的相似性尽量大，簇间数据样本之间的相似性尽量小，同时可以获得更具有平衡性的划分效果。研究表明，通过计算p-Laplacian矩阵的第二小特征向量，使用图划分标准Ccut能够获得更具有平衡性的聚类效果。但是，原p-谱聚类算法的相似性计算方法很难构造一个高质量的相似性矩阵来描述数据之间的内在关系，聚类效果对相似性计算方法是非常敏感的；再者，算法中相似性计算的方法与数据聚类的方法分别在两个不同的步骤中实现，故相似矩阵并不一定是适合此聚类方法的，从而有可能得不到最优的聚类效果[10]。

本文从一种新的视角出发来解决上述聚类问题。首先，通过数据样本与最优近邻之间的局部距离来优化相似性计算的方法，从而得到高质量的相似性矩阵[11]。假设数据样本之间距离越小，两者之间的相似性越大。再者，通过对p-Laplacian矩阵进行秩约束获得较为理想的近邻分配，可以实现在最终矩阵中连通分量的数目等同于聚类数目，即每一个连通分量对应一个簇。本文提出的基于局部相似性优化的p-谱聚类算法，能够同时实现相似性矩阵的计算以及对数据样本的聚类两个步骤，从而得出较优的聚类结果[12]。本文使用此聚类算法分别对人工数据集和UCI数据集进行实验，结果表明，基于局部相似性优化的p-谱聚类算法可以获得较好的更加具有平衡性的聚类效果。

本文组织结构如下：第2章介绍了p-Laplacian矩阵的概念，分析了p-Laplacian矩阵与齐格切之间的关系；第3章描述了局部相似性优化方法的理论基础，并提出了基于局部相似性优化的p-谱聚类算法；第4章通过实验验证了基于局部相似性优化的p-谱聚类算法的效果；最后对全文进行总结并讨论研究前景。

2 p-谱聚类

谱聚类的思想源于谱图划分理论。对于一个数据集，可以构造一个无向加权图G=(V,E)，其中顶点集合V表示数据样本，权值集合E表示数据之间的相似性。假设A是顶点集合V的子集，则A的补集可以定义为对于A和Aˉ之间的图划分目标函数可以表示如下[13]：

其中，wij表示顶点i和j之间的亲和度。

为了产生更加均匀的聚类效果，Shi和Malik在此基础上，进一步提出图划分标准规范切（normalized cut，Ncut），表达式如下[14]：

对该目标函数最小化意味着对类间数据样本相似度最小化，同时，最大化类内数据样本的相似度，故此图划分标准能够产生具有较好均衡性的划分结果。但此目标函数是投影矩阵的非线性函数，可能会存在局部极小值的问题。

为了进一步得到更具有平衡性的聚类效果，Cheeger等人提出齐格切图划分标准，Ccut的表达式如下[15]：

其中，|A|表示集合A中数据样本的数目。齐格切通过最小化表达式（3）的值来得到无向图的最优图划分结果，即簇内数据样本之间的相似度最大，簇间数据样本之间的相似度最小。但是根据Rayleigh商原则，计算无向图齐格切的最优划分结果是一个NP-难题[16]。接下来，将通过在谱聚类算法中引入p-Laplacian算子来近似得到齐格切的最优划分结果。

Heigh等人定义了p-Laplacian算子的内积形式，其表达式如下：

其中，p∈(1,2]；f是p-Laplacian矩阵的特征向量。

定理1对于任意p＞1以及顶点集合V的每一划分A和Aˉ，都存在一个与p-Laplacian矩阵相关的函数Fp(f,A)满足[17]：

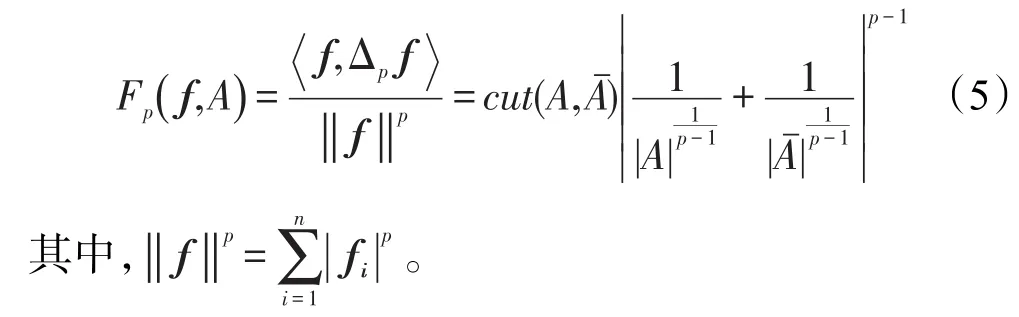
表达式（5）可以被看作一个具有较强平衡性的图划分标准，并且可以进一步得到：

由定理1可得，利用p-Laplacian算子，齐格切的最优划分可以在多项式时间内被计算得到。因此Fp(f)的解决方法是齐格切的一个近似最优解，以及最优解可以通过p-Laplacian矩阵的谱分解获得。

其中，λp是特征向量f对应的特征值。

特别的，通过p-Laplacian矩阵的第二小特征向量以及设定合适的阈值，可以对无向图进行二路划分。选择最优的阈值是能够最小化对应齐格切目标函数值的。对于p-Laplacian矩阵的第二小特征向量，其阈值应该满足：

3 局部相似性优化的p-谱聚类算法

3.1 局部相似性测度的优化

聚类算法中，对数据样本之间局部相似性的求解是一个复杂的过程。根据数据样本集合X={x1,x2,…,xn}，首先定义一个数据样本矩阵X∈Rn×d，然后对每个数据样本确定其第k近邻点。本文首先把数据样本集合X中的数据样本均看作xi的近邻点，并使用欧氏距离来表示相似性[18]，局部相似性用sij表示。通常，如果两个数据样本之间的欧氏距离较小，则表示两者之间具有较大的相似性另外，每个数据样本均可看作数据样本xi的相邻点，且具有相同的局部相似性可看作每个数据样本进行近邻分配的预操作。因此存在一种表示数据样本之间局部相似性的方法，满足下述表达式：

其中，si∈Rn×1表示向量，si的第j个元素表示数据样本i和j之间的局部相似性sij；γ是正则化参数；定义是特征向量，的第j个元素表示然后表达式（9）可被进一步转化为向量形式，其描述如下：

对于每个数据样本xi，可以使用表达式（9）为其分配近邻点。因此，可以通过表达式（11），为所有数据样本分配近邻点：

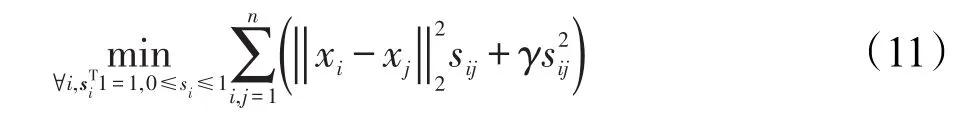
在理想情况下对数据样本进行近邻分配时，可以得到无向图G中连通分量的数目精确地等于聚类数目c。然而，通常情况下在使用表达式（11）进行近邻分配时，对于任意的γ值，很难实现都能在理想情况下进行分配。并且在大多数情况下，数据样本集合中所有数据样本只组成一个连通分量。为了实现在理想情况下进行近邻分配，表达式（11）的局部相似性应该被约束，以便于近邻分配能够变成一个数据样本自适应的过程，使得连通分量的数目精确地等于聚类数目c。因为这种对局部相似性的结构约束是根本性的难题，而且操作起来也是十分困难的，所以实现这种约束看起来像是一个不可实现的目标。本文将提出一个新颖而又简单的算法来实现这个目标。

近邻分配后，S∈Rn×n被定义为相似性矩阵。假设每个顶点用函数fi∈Rc×1表示，则下述等式是正确的：

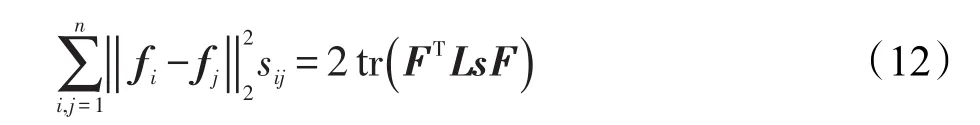
其中，F∈Rn×c，第i行等于fi。在图论中被定义为拉普拉斯矩阵，Ds∈Rn×n被定义为度矩阵，其第i行对角元素等于

如果相似性矩阵S是非负的，则对应拉普拉斯矩阵具有下述主要特性[20]。

定理2拉普拉斯矩阵Ls中，其特征值为0的数目c等于对应无向图G中连通分量的数目。

根据上述定理如果rank(Ls)=n-c，则表明近邻分配可在理想情况下进行，同时根据相似矩阵S能够成功把数据样本划分到c个簇中，并且在聚类过程中没有使用到k-means以及其他聚类算法。由定理2可知，可以把rank(Ls)=n-c看作约束条件添加到表达式（11）所描述的问题中来实现理想情况下的近邻分配。因此本文聚类算法可以解决下述表达式（13）需要解决的问题，表达式描述如下：

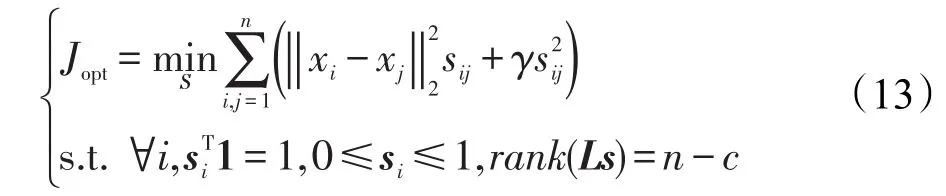
假设σi(Ls)表示拉普拉斯矩阵Ls的第i小特征值，由于Ls是半正定矩阵，故σi(Ls)≥0。对于一个足够大的数值λ，表达式（15）描述的问题可用表达式（14）表示：

当λ的值足够大时，已知σi(Ls)≥0，表达式（14）只要使趋于零就可以得到最优解S。

根据Ky Fan的理论分析[21]，有：

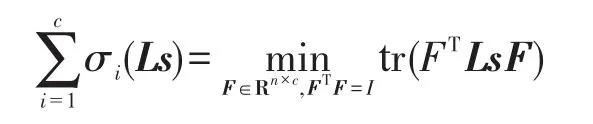
因此表达式（14）可以进一步转化为表达式（15），描述如下：

相对于原始表达式（13），表达式（15）更容易去解决。本文可以从下述选择一种最优的方法来解决问题。

当相似矩阵S不变时，则表达式（15）描述如下：

当F不变时，则表达式（15）描述如下：

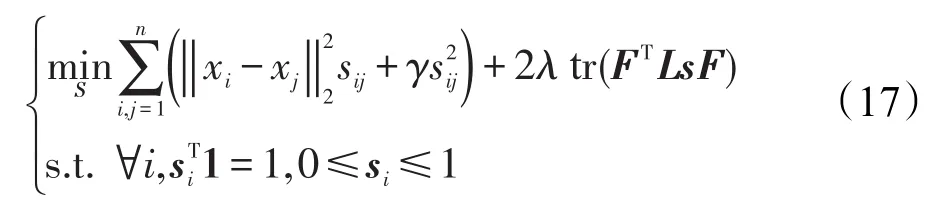
根据表达式（11），表达式（17）可转化为：

在表达式（18）中，每一个i都是相互独立的，因此对于i，可得下述表达式（19），描述如下：

由上述分析可知，得到相似矩阵S的算法1如下。

算法1计算相似矩阵S

输入：数据样本矩阵X∈Rn×d，聚类数目c，正则化参数γ，一个足够大的数值λ。

输出：具有c个连接部分的相似矩阵S∈Rn×n。

使用表达式（11）的最优解对S进行初始化；

如果不收敛，则：

（1）更新F。F由拉普拉斯矩阵的前c个最小特征值对应的特征向量组成；

（2）对于每个i，使用表达式（19）的最优解来更新相似矩阵S的第i行，其中di∈Rn×1为特征向量，其第j行元素等于

终止。

3.2 确定正则化参数γ的值

在实际情况下，由于正则化参数的取值范围是从零到无穷大，故对其进行训练确定值大小是非常困难的。本文提出一种有效的方法来间接确定正则化参数γ的值。

对于每个样本数据i，表达式（13）中的目标函数等价于表达式（10）中的目标函数，表达式（10）的拉格朗日函数表达式（21）描述如下：

其中，η和βi≥0是拉格朗日乘子。

根据KKT条件[22]，可以证实最优解si的表达式（22）可描述如下：

当实际算法运行时，如果进一步考虑数据样本的局部相似性，将会获得较好的聚类效果。因此，一般情况下更倾向于只考虑xi的k个最近邻，从而可以得到稀疏矩阵si；另一方面，聚类算法中使用稀疏矩阵还可以缓解设备的运算负担。

根据等式（22）和约束条件sTi1=1，有：

因此根据等式（23）和（24）可得关于γi的不等式如下：

在已知表达式（9）具有k个非零值的情况下，为了得到最优解si，γi可以用表达式（26）表示，描述如下：

对于γ的值等于γ1,γ2,…,γn的平均值，也就是说，γ可以用下述表达式（27）表示：

由于近邻数k是一个整数并且具有明确的实际意义，相对于γ，k是更容易通过训练得到的。

3.3 局部相似性优化的p-谱聚类算法

算法通过计算数据样本与最优近邻之间的局部距离来优化相似性矩阵，同时利用p-Laplacian矩阵的秩约束条件，使最终得到的矩阵中连通部分的数目精确等于聚类数目，从而进一步实现聚类效果的优化。它的主要思想是：首先根据优化后的局部相似性测度方法来计算数据样本之间的相似度，得到相似矩阵；接着计算p-Laplacian矩阵的特征值和特征向量，并递归地使用二分法进行划分来最优化目标函数；最终获得更好的聚类结果。

算法2优化的p-谱聚类算法

输入：数据样本集合X∈Rn×d，聚类数目c，正则化参数γ，一个足够大的数值λ。

输出：c个类C1,C2,…,Cc。

（1）根据算法1可得相似性矩阵S；

（2）初始化聚类C1=V,聚类数目s=1；

（3）重复步骤（3）～（7）；

（4）对每个类Ci(i=1,2,…,s)，最小化目标函数Fp(f)；

（5）对非规范化矩阵或规范化矩阵求解最优边值，从而得到图划分标准齐格切判据的近似解；

（6）利用图切判据的最小目标函数对Ci(i=1,2,…,s)进行分割；

（7）s⇐s+1；

（8）s==c时，循环结束，并输出聚类结果；

（9）利用聚类结果进一步得出衡量算法优越性的Ncut值。

4 实验仿真与结果分析

本文为了分析基于局部相似性优化的p-谱聚类算法的聚类效果，分别选取了4个人工数据集和两个模式识别测试数据集（简称UCI）进行实验，并与原p-谱聚类算法的聚类效果进行对比，从而体现基于局部相似性优化的p-谱聚类算法的优越性。实验过程中为了方便分析算法的优越性，p值始终保持不变。实验的计算机环境为：Intel Core i5-2450M 2.5 GHz CPU，内存6 GB,Windows 8.1 64位操作系统，运行平台为Matlab R2014a。

人工数据集是根据聚类需要进行人工合成的，一般情况下都具有相对复杂或者较为独特的数据结构，例如凸形结构、流形结构和多维结构等。一般的聚类算法往往都只能解决其中的少数问题，人工数据集对算法的要求非常严格，具有较强的挑战性。因此，可以通过对比原p-谱聚类算法和基于局部相似性优化的p-谱聚类算法在人工数据集上的聚类效果来分析后者的优越性与有效性。本文选取的4个人工数据集为Twomoon、Threecircle、Smile、Fourline，其特征如表1所示，其可视化分布如图1所示。

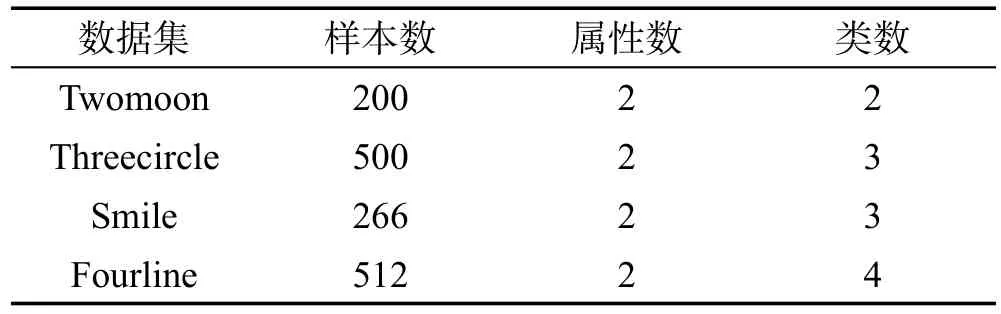
Table 1 Characteristics of artificial data sets表1 人工数据集及其数据特征

为了进一步验证基于局部相似性优化的p-谱聚类算法的优越性，从UCI数据集库选择两个真实的数据集进行实验。本文选取的两个数据集都是具有明确分类结果的，其具体特征如表2所示。

Table 2 Characteristics of UCI data sets表2 UCI数据集及数据特征

以上分别对4个人工数据集Twomoon、Threecircle、Smile、Fourline和两个UCI数据集Wine和USPS进行了描述和分析。接下来，分别使用原p-谱聚类算法和基于局部相似性优化的p-谱聚类算法对人工数据集和UCI数据集进行实验。为了验证算法的一般性，首先对4个人工数据集进行聚类，两种聚类算法的效果如图2所示，（a）表示数据集Twomoon的聚类效果，（b）表示数据集Threecircle的聚类效果，（c）表示数据集Smile的聚类效果，（d）表示数据集Fourline的数据效果。

从图2中可以看出，对于人工数据集，相对原p-谱聚类算法，基于局部相似性优化的p-谱聚类算法可以获得更好的聚类效果。

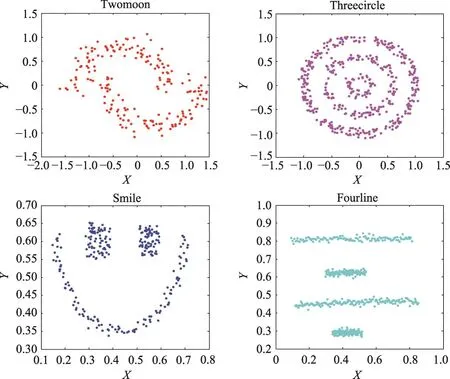
Fig.1 Distribution of artificial data sets图1 人工数据集的分布

Table 3 Ncutvalue of two algorithms on artificial data sets表3 两种算法在人工数据集得出的Ncut值

在本文实验中，根据第2章中图划分标准规范切和最终的聚类结果可以得出Ncut值，其大小能够作为衡量算法优越性的标准，即Ncut值越小，则算法越具有优越性、有效性。表3给出了两种聚类算法分别在4个人工数据集Twomoon、Threecircle、Smile、Fourline的Ncut值。

表3中，第一行数据表示原p-谱聚类算法在4个人工数据集上聚类后，得出的Ncut值，第二行数据表示基于局部相似性优化的p-谱聚类算法在4个人工数据集上聚类后，得出的Ncut值。从表中可以看出，对于人工数据集，后者的Ncut值明显小于前者，故基于局部相似性优化的p-谱聚类算法产生更好的聚类效果。

通过上述对人工数据集进行实验与分析，验证了本文的谱聚类算法的有效性。接下来，将使用两种聚类算法进一步对两个UCI数据集Wine和USPS进行聚类。

表4给出了两种聚类算法分别在两个UCI数据集Wine和USPS上的Ncut值。

Table 4 Ncutvalue of two algorithms on UCI data sets表4 两种算法在UCI数据集得出的Ncut值

Fig.2 Clustering results of two algorithms on artificial data sets图2 两种聚类算法在人工数据集的聚类效果

表4中，第一行数据表示原p-谱聚类算法在两个UCI数据集上聚类后，得出的Ncut值，第二行数据表示基于局部相似性优化的p-谱聚类算法在两个UCI数据集上聚类后，得出的Ncut值。从表中可以看出，对于UCI数据集，后者的Ncut值明显小于前者，故基于局部相似性优化的p-谱聚类算法产生更好的聚类效果。

经过上述实验仿真和结果分析可知，基于局部相似性优化的p-谱聚类算法具有更好的优越性和有效性。

5 结束语

本文提出了一种基于局部相似性优化的p-谱聚类算法。该算法通过数据样本的自适应和最优近邻之间的局部距离来优化相似性测度的计算方法，同时通过引入p-Laplacian矩阵的秩约束，可以得到聚类过程中无向图G中连通分量的数目精确地等于聚类数目，从而有效地解决了原p-谱聚类算法中不能充分挖掘数据集的局部结构信息和相似性矩阵的计算与数据样本的聚类分别在两个不同的步骤中实现，导致有可能得不到最优聚类效果的问题。为了验证基于局部相似性优化的p-谱聚类算法的优越性和有效性，在本文实验中，采用了4个人工数据集和两个UCI数据集分别进行实验，并且将聚类效果与原p-谱聚类算法的聚类效果进行了对比。从实验仿真与结果分析中可知，基于局部相似性优化的p-谱聚类算法具有更好的优越性和有效性。接下来的工作是通过分析研究特征向量的结构信息来自动确定数据集的聚类数目，从而获得更好的聚类效果。

[1]Johnson S C.Hierarchical clustering schemes[J].Psychometrika,1967,32(3):241-254.

[2]MacQueen J.Some methods for classification and analysis of multivariate observations[C]//Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability,Berkeley,1965.Berkeley:University of California Press,1967:281-297.

[3]Benhur A.Support vector clustering[J].Journal of Machine Learning Research,2002,2(2):125-137.

[4]Nie Feiping,Xu Dong,Li Xuelong.Initialization independent clustering with actively self-training method[J].IEEE Transactions on Systems,Man and Cybernetics:Part B,2012,42(1):17-27.

[5]Cai Xiao,Nie Feiping,Huang Heng.Multi-viewK-means clustering on big data[C]//Proceedings of the 23rd International Joint Conference on Artificial Intelligence,Beijing,Aug 3-9,2013.Menlo Park:AAAI,2013:2598-2604.

[6]Jia Hongjie,Ding Shifei,Xu Xinzheng,et al.The latest research progress on spectral clustering[J].Neural Computing&Applications,2014,24(7/8):1477-1486

[7]Zhang Xianchao,You Quanzeng.An improved spectral clustering algorithm based on random walk[J].Frontiers of Computer Science in China,2011,5(3):268-278.

[8]Jia Hongjie,Ding Shifei,Meng Lingheng,et al.A densityadaptive affinity propagation clustering algorithm based on spectral dimension reduction[J].Neural Computing&Applications,2014,25(7/8):1557-1567.

[9]Bühler T,Hein M.Spectral clustering based on the graphp-Laplacian[C]//Proceedings of the 26th Annual International Conference on Machine Learning,Montreal,Jun 14-18,2009.New York:ACM,2009:81-88.

[10]Zelnik-Manor L,Perona P.Self-tuning spectral clustering[C]//Proceedings of the 2004 Conference on Neural Information Processing Systems,Vancouver,Dec 13-18,2004:1601-1608.

[11]Jia Hongjie,Ding Shifei,Du Mingjing.Self-tuningp-spectral clustering based on shared nearest neighbors[J].Cognitive Computation,2015,7(5):622-632.

[12]Nie Feiping,Wang Xiaoqian,Huang Heng.Clustering and projected clustering with adaptive neighbors[C]//Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,New York,Aug 24-27,2014.New York:ACM,2014:977-986.

[13]Donath W E,Hoffman A J.Lower bounds for the partitioning of graphs[J].IBM Journal of Research&Development,1973,17(5):420-425.

[14]Shi J,Malik J.Normalized cuts and image segmentation[J].IEEE Transactions on Pattern Analysis&Machine Intelligence,2000,22(8):888-905.

[15]Amghibech S.Bounds for the largestp-Laplacian eigenvalue for graphs[J].Discrete Mathematics,2006,306(21):2762-2771.

[16]Ding Shifei,Jia Hongjie,Zhang Liwen,et al.Research of semi-supervised spectral clustering algorithm based on pairwise constraints[J].Neural Computing&Applications,2014,24(1):211-219.

[17]Hagen L,Kahng A.Fast spectral methods for ratio cut partitioning and clustering[C]//Proceedings of the 1991 International Conference on Computer-Aided Design,Santa Clara,Nov 11-14,1991.Piscataway:IEEE,1991:10-13.

[18]Ding Shifei,Jia Hongjie,Du Mingjing,et al.p-spectral clustering based on neighborhood attribute granulation[C]//Proceedings of the 9th IFIP TC 12 International Conference on Intelligent Information Processing,Melbourne,Nov 18-21,2016.Berlin,Heidelberg:Springer,2016:50-58.

[19]Shi Jianbo,Malik J.Normalized cuts and image segmentation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2000,22(8):888-905.

[20]Hein M,Audibert J Y,Luxburg U V.Graph Laplacians and their convergence on random neighborhood graphs[J].Journal of Machine Learning Research,2007,8(9):1325-1370.

[21]Ding Shifei,Qi Bingjuan,Jia Hongjie,et al.Research of semi-supervised spectral clustering based on constraints expansion[J].Neural Computing&Applications,2012,22(1):405-410.

[22]Boyd S,Vandenberghe L.Convex optimization[M].Cambridge:Cambridge University Press,2004.