基于Petri网的最大流-最小割问题建模与求解
, ,
(1.福建工程学院 信息科学与工程学院, 福建 福州 350118; 2.福建工程学院 福建省大数据挖掘与应用技术重点实验室, 福建 福州 350118; 3.中南大学 信息科学与工程学院, 湖南 长沙 410083; 4.长沙理工大学 计算机与通信工程学院, 湖南 长沙 410076 )
图论中有许多经典的问题,包括最短路径问题、最大流-最小割问题等。对于这些问题,学者们有过大量的研究并提出了一系列求解办法。Petri网(PN)是一种可以用图形表示的数学对象,具有深刻的数学内涵基础,这使得它在形式化和求解图论问题时具有极大的优势。近年来,已
有许多将PN与图论问题相结合的研究成果,例如:文献[1]使用PN对代谢路径进行建模仿真,其中应用图的最大割来处理超过一定长度和宽度的代谢路径;文献[2-3]将PN应用于故障树形图分析中,用以实现系统最小割集的求解;文献[4]将粗糙集理论与PN相结合进行随机流网络可靠性评价。但是国内外基于PN的最大流-最小割问题研究并不多见,相关理论也有待完善。
最大流(max-flow)与最小割(min-cut)问题是一类典型的对偶问题,涉及计算机、图论和运筹学,是一类经典的组合优化问题,也可以认为是特殊的线性规划问题[5]。在图形[6]、图像分割[7-8],交通运输网络分析[9-10]等诸多控制、决策领域有着广泛的应用。经典的解决方法有预流-推进法(preflow push method)、增广路径法(augmenting path method)等。该问题可进一步扩展到不确定图最可靠最大流问题[11],节点和边都有容量的有向平面网络中的最小截和最大流问题[12]等。文献[4- 5]与本文研究工作有着较高的相关度:文献[4]简单描述了一种使用PN来表示流网络的方法,但其研究重点在于对随机流网络可靠性进行分析,所以在有关系统模型的含义及系统模型准确性等方面并未深入研究;文献[5]所提出的流网络PN模型可以说是[4]中模型的一种改进,但为求最大流,用户需事先确定“拥堵结点”,并进行一系列的设置,且不论其提出模型的准确性和完整性,该方法中过多的人为干预对问题的求解与表达十分不利。
本文在增广路径法思想的基础上给出了最大流-最小割问题的一种PN形式化表达,通过相关分析、证明深入阐述了其中的机制与原理。该模型无需额外的控制机制,能够有效解决最大流-最小割问题。
1 基本性质
1.1 问题的定义
1.1.1 流网络、流及流的值
定义1[13]流网络G=(V,E)是一个有向图,其中每条边(u,v)∈E均有一非负容量c(u,v)>0。如果E包含一条边(u,v),则绝不会存在与其方向相反的边(v,u)。如果(u,v)∉E则c(u,v)=0。且决不允许存在自循环的边。流网络中有两个特別的顶点:源点s和汇点t。每个顶点均处于从源点到汇点的某条路径上。
定义2[13]设G=(V,E)是一个流网络,其容量函数为c。设s为网络的源点,t为汇点,则G的流是一个实值函数f:V×V→R,且满足下列两个性质:
容量限制:对所有u,v∈V,要求
0≤f(u,v)≤c(u,v)
流守恒性:对所有u∈V-{s,t},要求
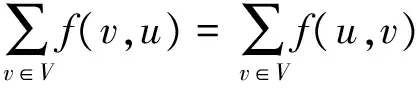
非负值f(u,v)称为从顶点u到顶点v的流。如果(u,v)∉E,则从u到v没有流,且f(u,v)=0。
定义3[13]流f的值|f|定义为
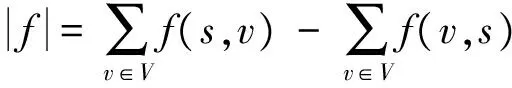
一般来说,一个流网络中进入源点的总流为0,因此流的值为从源点出发的总流,也等于进入汇点的总流。
1.1.2 最大流问题
通过上述定义可以引出最大流问题的描述:给出一个具有源点s和汇点t的流网络G,希望找出从s到t的最大值流。在某些应用中,也许仅仅知道最大流就满足要求了,但一般情况下,希望知道达到该值的流(边流量值)[14]。
图1(a)是文献[13]中关于流网络所举的一个例子,简单来说其模型化描述了这么一个实际问题:Lucky Puck公司需要将他们所制造的冰球通过卡车从生产地s运送到仓库所在地t。因为卡车按指定路线(边)在两城市(顶点)间行驶且其容量有限,所以每天在每城市u和v之间至多装运c(u,v)箱产品(用数字标识于有向边上)。他们的目标是确定每天所能运输的最大箱数,并按这一数量进行生产。
文献[15]指出:Petri网不仅仅是一种可以用图形表示的数学对象,它首先是一种物理对象,因为它把尊重自然规律作为第一要义。一个好的系统模型不能只存在于纸面上,活跃于论文中。它必须能够用来描述物理世界的客观存在,使客观存在成为论文的研究对象。下节将介绍使用PN对上述实际问题的形式化描述。
1.2 Petri网
有关PN的基础概念详见文献[15],本节只对本文涉及到的性质及主要概念进行介绍。令N=(P,T;F)是一个Petri网(简称为网),P、T及F分别指代库所、变迁和有向弧。Σ=(N,K,W,M0)是一个网系统,其中K,W和M0依次是N上的容量函数、权函数和标识。M0称为Σ的初始标识。
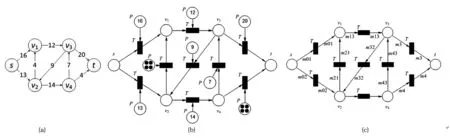
(a)文献[13]中关于Lucky Puck公司卡车运输问题的流网络f; (b),(c) 本文所提出的关于f的两种PN形式化描述图1 一个流网络的实例Fig.1 Demonstration of the flow network
为应用系统建立PN模型,首要需决定什么是系统的变迁,什么是系统的库所。流网络中具有顶点、边及边上的容量等元素,而PN中的库所可以用来表示存放资源的场所,变迁则可以代表某种行为的发生过程。
因此使用PN来形式化流网络的一种方法是使用变迁和有向弧来表示流网络的边和资源流动的行为;用一类库所(图1(b)中的s,v1等)来表示流网络中的顶点,另一类库所(图1(b)中的P)来表示边上的容量限制。那么,网络中的流对应着资源托肯按照变迁规则从一个顶点库所转移至另一顶点库所。依照该思想可以将图1(a)问题转换为图1(b)中的PN模型。
图1(c)展示了流网络的另一种PN形式化表示,仍使用库所表示顶点,变迁代表资源流动的过程,与图1(b)中不同的是这里使用弧上的权函数W(可以是标量或者如图1(c)中m01等所标识的变量,但权值不大于边容量)来表示流网络边上的实际流量。本文将采用图1(c)中的方法来表示流网络,关于权函数W的设置将在第3节进行相应的陈述。
2 最大流-最小割问题建模与分析
L R Ford和 D R Fulkerson在 1962年提出了解决最大流问题的一种有效途径。这是一种沿着从源点到汇点的路径上不断增加流量的通用方法,它是许多算法的基础。在一般文献中称之为Ford-Fulkerson方法,即增广路径方法。
本文采用与增广路径方法类似的思想来构造流网络的残留网络PN模型,并求解最大流-最小割问题。为了便于类比,首先给出增广路径方法的伪代码。
算法1 FORD-FULKERSON-METHORD.
输入:流网络G,源点s,汇点t
输出:流f
1 BEGIN流f为0
2 WHILE残留网络Gf中存在一条增广路径p
3 DO 沿路径p增加流f
4 END
2.1 基于PN的残留网络建模
本节讨论对流网络G所对应的残留网络Gf建模。由于Gf不仅包含原网络中的边,还包含其反向边,因此可以通过修改图1(b)中模型来构造流网络的残留网络模型。其详细过程如下:
(1)对于流网络G=(V,E),对其任意顶点v∈V,构造所对应的库所Pv;对于u,v∈V且(u,v)∈E,构造变迁和弧连通库所Pu,Pv,弧的方向与(u,v)方向一致,将该类变迁统一记作T。
(2)为每个T构造一个前集库所,统一记作P,代表边上的容量,且初始化资源数为所对应边上的容量数;为每个T构造一个后继库所,统一记作P′,初始化资源数为0。图2(a)所示为(u,v)∈E且v=t的情况。
(3)进一步构造除包含汇点t外的所有边所对应的反向边模型。对所有(u,v)∈E∧v≠t,添加变迁T′使得·T′={Pv,P′},T′·={Pu,P},如图2(b)所示。其中·T′和T′·分别代表T′的前集和后集。
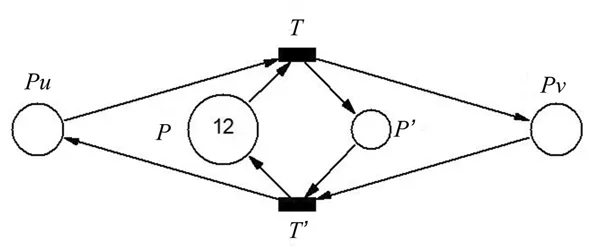
(a)两邻接顶点之一是汇点的情况
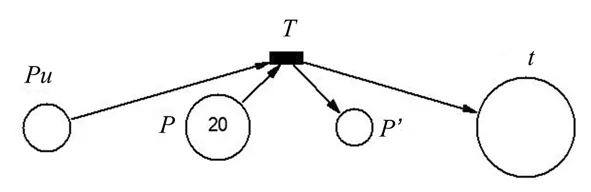
(b)其他情况图2 残留网络PN模型中两邻接顶点之间的关系图Fig.2 Two cases of two neighbouring vertexes in the residual network PN Model
因此,在残留网络Petri网模型中,任意边的两端顶点有且仅有2种关系:要么如图2(a)所示(两个顶点其中一个为汇点t),要么如图2(b)所示(其他情况)。值得注意的是,库所P与P′有多重含义:以图2(b)为例,P中资源数目既标识了边(u,v)上的残留容量(residual capacity)又可看作边(v,u)上的流。P′中资源数目在标识边(u,v)上流的同时又可表示边(v,u)上的残留容量。另外,从PN原理角度来看,P与P′互为补库所,从而避免了冲撞的发生,为系统的安全性提供了保障[16]。按照上述构造规则,图3(a)展示了图1(a)中流网络所对应的残留网络在某一状态标识下的PN模型。为了模拟资源的流动,给予s对应库所初始状态标识为一远大于最大流的数,这里取值100。
2.2 模型分析及证明
本文给出了流网络及其残留网络的PN模型,以描述物理世界的客观存在,即系统模型的仿真性。下面通过相关的分析及证明来确保所给模型的正确性。
按照资源在PN中流动的法则,在不受任何外部因素控制下,残留网络PN系统最终可以达到并总是处于一系列状态,这类状态的一个共同特点是系统的一些顶点库所中不会再有资源流动,这为寻找最大流和最小割提供了帮助。后面将证明,对于流网络G=(V,E),如果其残留网络PN模型中一些顶点库所中不再有资源流动,则意味着已经找不到任何路径使得资源从s到t。这些资源不再流经的顶点(例如图3(a)中的v3)与汇点t组成一个集合Ct,其余顶点为另一个集合Cs=V-Ct,则Ct、Cs是G的一个最小割集。
众所周知,一个最大流量经常对应着多个最大流分布。事实上,如果上述集合Cs中资源全部回流至源点,则该过程中不同的返回路径选择将对应不同的最大流分布。例如,当图3(a)所示顶点v1,v2,v4中资源全部流回至s中,则只可能存在3种可能性(使用箭头代表资源流向):(1)1个资源v4→v2,2个资源v2→s,1个资源v1→s;(2)1个资源v4→v2,1个资源v2→s,1个资源v2→v1,2个资源v1→s;(3)1个资源v4→v2,2个资源v2→v1,3个资源v1→s。他们分别对应于图3(b、c、d)所示的流网络中3种最大流分布。因此,特定的最大流分布可以通过特定回流路径的决策选择进行获取。
前面从直观分析的角度阐述了一些观点,下面通过证明来进行论述。
首先需要关注的是PN模型中元素在实际问题中的意义,关于P′及P类库所中资源数的含义在2.1节已经详细论述过,为了方便引用,将其表述为性质1。其正确性从残留网络PN模型的构造规则及定义2易得。
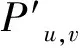
引理1残留网络的PN模型中,资源托肯从s到t的所经过的路径等价于一条增广路径。
证明 不妨令残留网络的PN模型中,资源托肯从s到t有一条路径p′,则总可以找到一条从s到t简单路径p,使得p与p′等价:
如果p′是一条简单路径,那么p=p′。
如果p′是含有一条环路的路径,不妨设vi处存在环路vi→vj→vi(如图4所示),首先根据残留网络构造规则,vi必不等于t(因为t处不会存在环路)。由构造规则(3)易知,资源从vi出发经由环路再回到自身前后,环路上的资源状态不会发生改变。因此删除环路后的简单路径p与原路
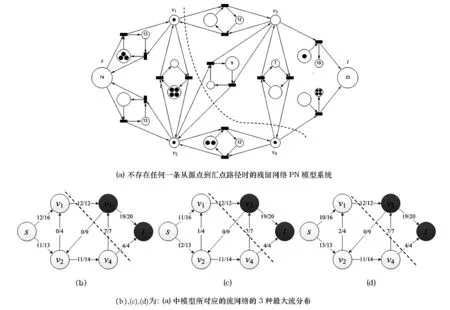
图3 基于残留网络PN模型的最大流求解Fig.3 Residual network PN model based maximum flow solution
径p′等价。
如果p′是含有多条环路的路径,则删除所有环路后的简单路径p与p′等价。
增广路径定义为残留网络中从s到t的一条简单路径。因此,综上所述,残留网络的PN模型中,资源托肯从s到t的所经过的路径等价于一条增广路径。证毕。
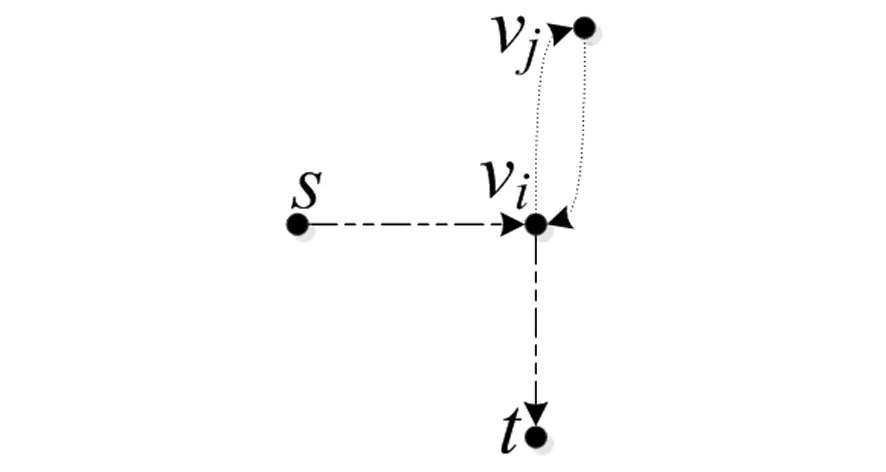
图4 残留网络中从s到t的某条包含环路的路径Fig.4 A case of a path from s to t with loops in the residual network
引理2残留网络的PN模型中,每单位资源托肯从s到达t等价于在对应的增广路径上增加一个单位的流。
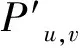
因此,每个单位资源托肯从s到达t,等价于其所确定的一条增广路径上相应的P类或者P′类库所中增加一个托肯,即路径的边上增加一个单位流。证毕。
定理1当残留网络PN模型找不到任何路径联通s与t时,网络达到最大流,t中的资源数等于最大流值。
分析 可以通过证明该方法与算法1所示增广路径方法等价来求证。
证明 由引理1和2可知,残留网络中单位资源从s到达t等价于找到了一条增广路径,并沿该路径增加了一个单位的流。随着从s出发的资源逐步流入t中,最终将找不到这样的一条路径。因此该方法与增广路径方法等价。
增广路径方法中找不到任何从s到t的增广路径时,网络达到最大流。相应的,残留网络PN模型找不到任何路径联通s与t时,网络达到最大流。根据定义3,最大流值等于所有进入汇点的流,即残留网络PN模型中t对应库所中的资源数。证毕。
定理2残留网络PN模型中的最大活的(live)子图所含顶点集合Cs与其余顶点集合Ct构成了流网络的最小割(Cs,Ct)。
证明 活系统要求每个变迁在任何可达标识下都是潜在可发生的。
当流网络G对应残留网络PN模型找不到任何路径联通s与t时,记Cs={v∈V:残留网络PN模型中从s到v存在一条通路}并且Ct=V-Cs。由残留网络的构造规则可知,如果资源可以从s流至v,那么也可以从v流回s,因此Cs为其最大活的子图所含顶点集合。
因为s∈Cs∧t∉Cs,所以划分(Cs,Ct)是一个割。它对应与增广路径法得到的一个最小割。证毕。
至此,已经论述如何使用PN求得任意流网络的最大流值和最小割集,图3中的虚线标明了流网络的一个最小割。但是实际应用中往往希望知道达到该值时各条边上的实际流量值。性质1表明,P′类库所中的资源数代表了流网络边上的流。所以当网络达到最大流时P′类库所中的资源数就是该问题的解。方法是当残留网络PN模型中找不到任何从源点到汇点的路径后,引导顶点库所中的资源全部回流至源点,使得除s,t外的顶点库所不再含有资源托肯。图5给出了结合流网络及其残留网络并包含资源回流机制的完整PN模型,下节将进行详细介绍。
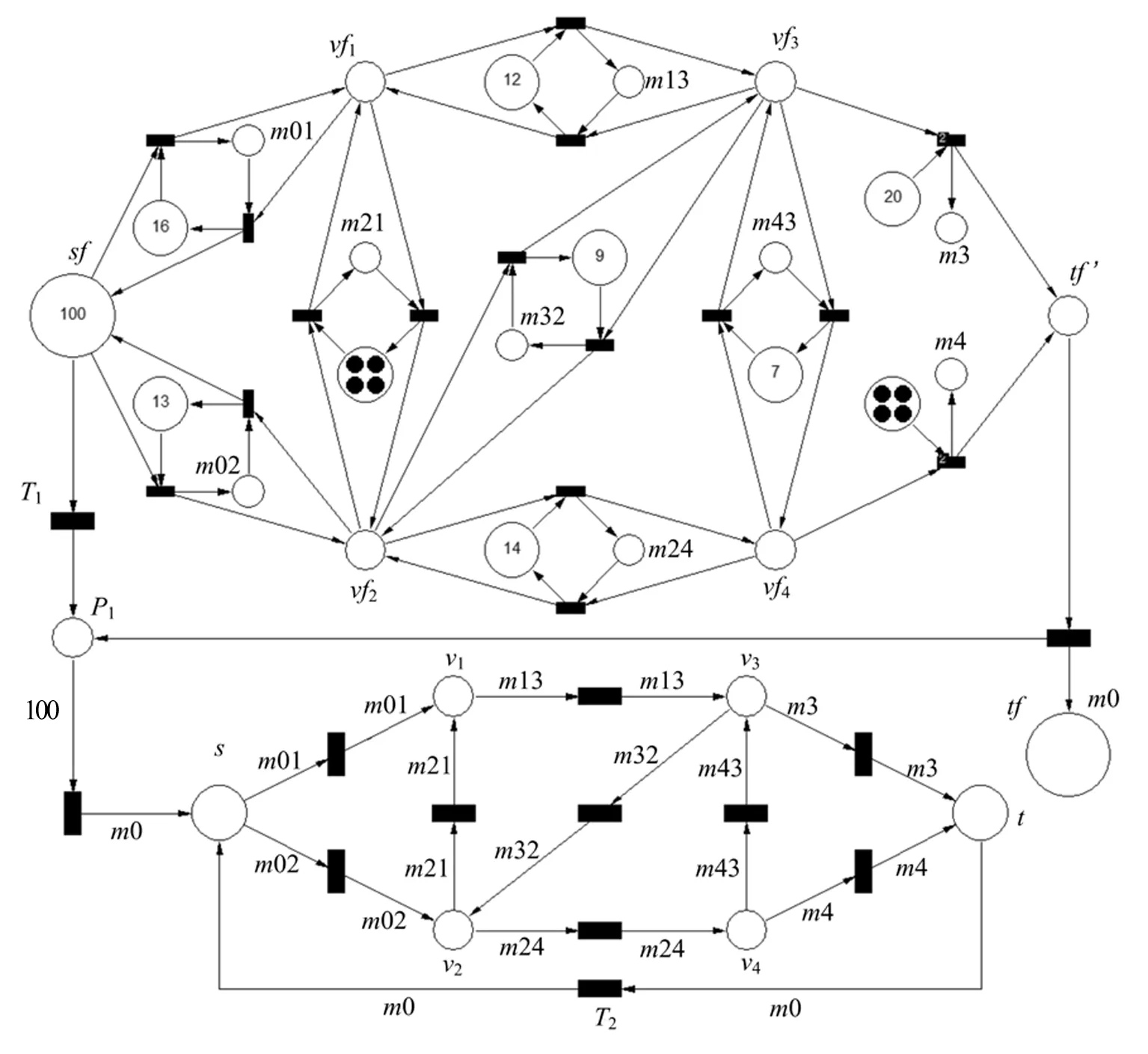
图5 流网络最大流-最小割问题完整的PN模型Fig.5 An integrated PN model that describes and solves the max-flow/min-cut problem for a given flow network
3 基于PN的最大流-最小割问题求解
本节将结合2.2节所提出的残留网络PN模型以及图1(c)所示的流网络PN模型对给定的流网络进行仿真求解。其中,求解的过程是通过资源托肯在残留网络PN模型系统(即图5上半部分)中的流动来实现的,而流网络PN模型系统(即图5下半部分)则主要用于对所求得的最大流及其分布进行展示。
以图1(a)的流网络为例,能够求得并展示:(1)两个最小割集;(2)流网络的最大流值;(3)某一流分布。具体来说,首先在残留网络PN模型的源点库所sf中指定足够数量的托肯(例如图5中所初始指定的100个托肯),当大量托肯经过一段时间的流动以后,模型中的顶点库所将会分为有资源流经和没有资源流经的两类,由定理2可知,这两个集合即为所求的两个最小割集。其次,在获得最小割的同时残留网络PN模型系统也将达到最大流状态,为了获得该最大流值,添加如图5中tf所示的库所。当达到最大流状态时tf中的资源数将等于所有进入汇点库所tf′的资源数,即最大流值。最后,为了确定所有边上的实际流量值(即流分布),为源点库所sf添加一个如图5中T1所示的后继变迁,从而使得所有剩余资源都经由sf到达P1的目的。当P1中资源数达到sf中初始资源数时,所有P′类库所中的资源数(即图5上半部分中m01等变量所代表的数值)都将确定下来,这些数值即为最大流的分布。
通过上述残留网络PN模型系统获得的数据可以在如图5下半部分所示的流网络中进行展示。例如最大流的值被作为源点库所s的初始资源数,m01、m02等流分布值将被指定为对应边的权值。另外,新添加的变迁T2使得最大流从源点到汇点后能够进入下一次的循环,正如Lucky Puck公司卡车运输问题中第2天需要按照前1天相同的运输方案继续运送冰球一样。
4 结语
本文在增广路径法思想基础上给出了最大流-最小割问题的PN形式化描述及其求解方法,包括流网络及其对应残留网络PN模型的构造流程,PN模型各元素在问题中代表的实际意义分析,并给出了获取最大流各个分布的方法,证明了PN模型中达到最大流的条件和通过活性分析可以得到一个最小割的结论,最后将残留网络和流网络PN模型结合起来给出最大流-最小割问题完整的解决方案。
将PN应用于最大流-最小割问题的优越性主要体现在:(1)PN对实际问题形式化表述时的直观性;(2)PN拥有S_补、活性分析等独特的系统建模和分析功能支持;(3)PN仿真过程易于从局部着手表现所模拟对象的动态变化等。因为最大流-最小割问题可以进一步扩展为最小费用最大流问题,不确定图最可靠最大流问题,节点和边都有容量的有向平面网络中的最小割和最大流等问题,这类问题的PN形式化建模与求解有着可观的研究价值,也为下一步工作提供了可行的研究方向。
[1] GENRICH H, KÜFFNER R, VOSS K. Executable Petri net models for the analysis of metabolic pathways[J]. International Journal on Software Tools for Technology Transfer, 2001, 3(4): 394-404.
[2] 尹延通,刘高飞,季亮.基于最小割集的光学测云系统故障诊断[J].延边大学学报(自然科学版),2016,42(3):267-270.
[3] 张永发,蔡琦,赵新文.应用Petri网模型改进最小割集的算法[J].核动力工程,2007,28(5):63-68.
[4] 刘玲艳,吴晓平,田树新.基于粗糙集和Petri网的随机流网络可靠性评价方法[J].控制与决策,2010,25(8):1273-1276.
[5] 胡雄鹰,胡斌,张金隆,等.基于Petri网求解网络最大流的并发仿真方法[J].武汉理工大学学报(信息与管理工程版),2010,32(1):27-30.
[6] FAN L, LIU K. Paint mesh cutting[J]. Computer Graphics Forum, 2011, 30(2): 603-611.
[7] 刘松涛,殷福亮.基于图割的图像分割方法及其新进展[J].自动化学报,2012,38(6):912-922.
[8] DELONG A, OSOKIN A, ISACK H N, et al. Fast approximate energy minimization with label costs[C]∥ IEEE Conference on Computer Vision and Pattern Recognition, IEEE, 2012: 1-27.
[9] 向红艳,张邻,杨波.基于最大流的路网结构优化[J].西南交通大学学报,2009,44(2):284-288.
[10] 寇玮华,李宗平.运输网络中有流量需求的转运结点最大流分配算法[J].西南交通大学学报,2009,44(1):118-121.
[11] 蔡伟,张柏礼,吕建华.不确定图最可靠最大流算法研究[J].计算机学报,2012,35(11):2371-2380.
[12] 张宪超,江贺,陈国良.节点和边都有容量的有向平面网络中的最小截和最大流[J].计算机学报,2006,29(4):544-551.
[13] CORMEN T H, LEISERSON C E, RIVEST R L, et al. Introduction to algorithms, Third[M]. London: The MIT Press, 2009.
[14] SEDGEWICK R.算法:C语言实现(第5部分:图算法)[M].霍红卫,译.北京:机械工业出版社,2010.
[15] 袁崇义. Petri 网原理与应用[M].北京:电子工业出版社,2005.
[16] 刘石坚,乐晓波,邹峥.关于 Petri 网系统S-补相关定理的补充证明及其分析[J].系统仿真学报,2009,40(S2):1-5.

