复合MLINEX对称损失函数下Pareto分布参数的Bayes估计

朱宁，刘庆华，农以宁，蒋东云

（桂林电子科技大学数学与计算科学学院，广西桂林541004）

0　引言

帕累托（Pareto）分布是收入分配理论中的一种重要的统计分布,最初是由意大利Pareto作为收入分布于1897年提出来的，并指出其是一个具有递减的失效函数[1]。自从Pareto分布提出以来就被广泛地运用于金融、保险、灾害预测等诸多领域，关于其统计推断的研究引起了很多学者的关注。近年来，在Bayes思想下Pareto分布参数估计的研究越来越多。韩慧芳等[2]研究了当尺度参数已知时，Pareto分布中形状参数的估计，一致最小方差无偏估计，并在平方损失和熵损失下讨论其可容许等。韦程东等[3]在复合LINEX对称损失函数下，研究Pareto分布在其尺度参数已知的情况下利用共轭先验分布求出其形状参数的E-Bayes估计。井晓培和周菊玲[4]讨论了独立同分布样本情形广义Pareto分布参数的经验Bayes单侧检验问题，并证明了此经验Bayes检验函数的渐近最优性，获得了其收敛速度。沈新娣和丁帮俊[5]研究Pareto分布在逐步Ⅱ型区间删失的情形下参数的估计和性质。韩明[6]研究Pareto分布中形状参数的估计、一致最小方差无偏估计。并分别在平方损失和熵损失下讨论了θ的Bayes估计,研究其容许性。

自从2003年Podder CK[7]提出MLINEX函数以来，越来越多的学者关注MLINEX函数。Podder CK[8]比较Pareto分布参数估计在MLINEX函数和平方损失函数下的不同。任海平[9]分别在加权平方损失函数和MLINEX损失函数下一类分布族参数的Minimax估计。金秀岩[10]在MLINEX损失函数的基础上，结合张睿[11]提出的复合LINEX对称损失函数的方法，定义了复合MLINEX对称损失函数，并在该损失函数下得到了对数伽玛分布尺度参数的Bayes估计、E-Bayes估计、多层Bayes估计等。

本文在金秀岩[10]提出的复合MLINEX对称损失函数的基础上，研究两参数Pareto分布的Bayes估计问题，在给定先验分布为Gamma分布的基础上给出Pareto分布参数的Bayes估计，并证明其容许性。最后在给定三类不同超参数先验密度函数下，给出其E-Bayes估计和多层Bayes估计并对估计的性质进行研究。

1　参数θ的Bayes估计

定义1[1]：设X为随机变量，若其分布函数为F(x)=为形状参数，λ为尺度参数且为门限参数。则称X服从两参数θ，λ。则称为Pareto分布，简称PD(θ,λ)。

设x1,x2,…,xn为来自PD(θ,λ)的独立样本，则其联合密度为：

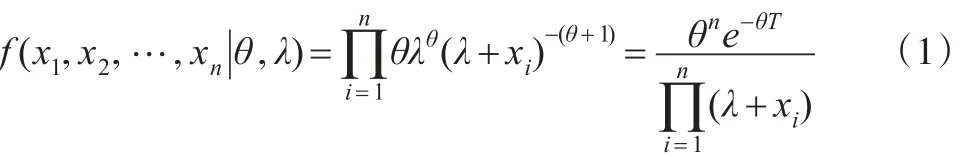
下页图1给出了在尺度参数λ=100时，形状参数θ分别取0.5、1、2时的Pareto分布的密度函数图像。由图1可以看出Pareto分布的密度函数是单调递减的函数。

定义2[11]：Mlinex非对称损失函数定义为：

图1Pareto分布的密度函数图像（λ=100）

δ为参数θ的估计，c是一类非对称损失函数。

定义3[10]：设损失函数Lc(θ,δ)由式（2）给出，则损失函数（3）称为复合Mlinex对称损失函数（见图2），其中δ为参数θ的估计。

图2复合MLINEX对称损失函数图像（w=1）

引理1：在损失函数（3）和模型f(x;θ,λ)=θλθ(λ+x)-(θ+1)下，若在空间中存在参数θ的估计量δ，其Bayes风险r(δ)＜+∞，则对于θ的任何先验分布π(θ)，θ的唯一Bayes估计的一般形式为：

证明：具体证明与金秀岩在文献[10]中的引理2.2的证明类似。

定理1：设x1,x2,…,xn是PD(θ,λ)的一组观察值，形状参数θ（尺度参数λ已知）的先验分布π(θ)服从Gamma

证明：由题意知,形状参数θ（尺度参数λ已知）的先验分布π(θ)服从Gamma分布Γ(a,b)，则θ的密度函数为：

根据样本联合密度函数（1），并结合式（4），得到θ的后验密度函数为：

则θ的后验分布密度服从以b+T为尺度参数，以n+a为形状参数的Gamma分布。

由θ的唯一Bayes估计的一般形式及θ的后验分布密度有：

将式（5）代入到式（6）可得：

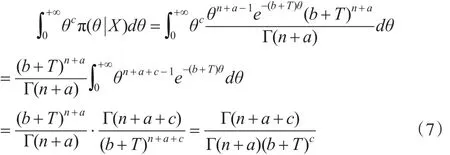
同理：

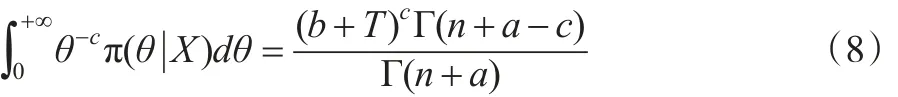
将式（7）和式（8）代入式（6），则：

综上所述，形状参数θ的Bayes估计为：

定理2：在给定先验分布π(θ)和损失函数L(θ,δ)下，参数θ的Bayes估计是可容许的。

证明：对于Bayes估计的Bayes风险小于或者等于任何估计的Bayes风险，只需证明存在一个θ的一个估计δ，其Bayes风险r(δ)＜∞，于是可得r()＜∞，从而是可容许的。

由题意知：

令δ=1，将其代入式（9），得到：

因为对于给定的样本值，r(1)存在且有界，即r(1)＜∞。因此r(δ)＜∞。又因为r)＜r(δ)，则r()＜∞，故是可容许的。

2　参数θ的E-Bayes估计

下面引入形状参数θ的E-Bayes估计的定义。

定义4[10]：对(a,b)∈D，若(a,b)是连续的，则称参数θ的E-Bayes估计。存在的，D为超参数a和b取值的集合D={(a,b)|0＜a＜1,0＜b＜m,m＞0}，π(a,b)是a和b在集合D上的密度函数，(a,b)为参数θ的Bayes估计。

定理3：对于服从Pareto分布的样本数据x1,x2,…,xn，若形状参数θ服从Gamma分布，则θ的先验密度

（1）若超参数a和b的先验密度函数为：

则参数θ的E-Bayes估计为：

（2）若超参数a和b的先验密度函数为：

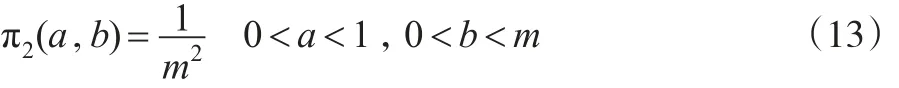
则参数θ的E-Bayes估计为：

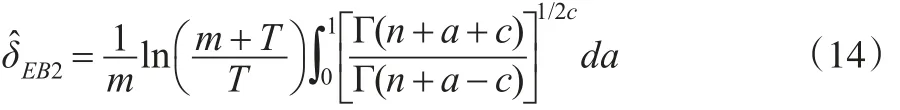
（3）若超参数a和b的先验密度函数为：

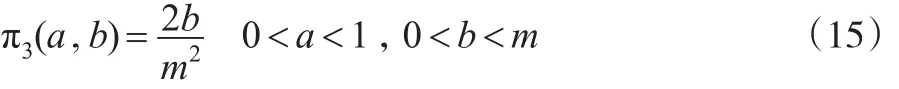
则参数θ的E-Bayes估计为：

若超参数a和b的先验密度函数π1(a,b)由式（11）给出，则参数θ的E-Bayes估计为：

（2）同理，若超参数a和b的先验密度函数π2(a,b)由式（13）给出，则参数θ的E-Bayes估计为：

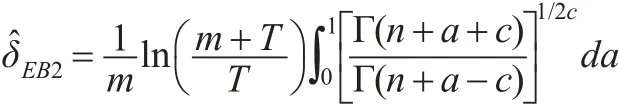
（3）同理，若超参数a和b的先验密度函数π3(a,b)由式（15）给出，则参数θ的E-Bayes估计为：

3　参数θ的多层Bayes估计

若形状参数θ服从Gamma分布Γ(a,b)，则其先验密度函数给定，那么如何确定超参数a和b？Lindley和Smith（1972）提出了多层先验分布的想法，即在先验分布中含有超参数时，可对超参数再给出一个先验分布。

其中，0＜θ＜∞。

在以上三个不同的多层密度函数的基础上，给出以下形状参数θ的三个不同的多层Bayes估计。

定理4：对于Pareto分布下的样本数据x1,x2,…,xn，若Pareto分布的形状参数θ的多层先验密度函数分别为式（17）至式（19），则在复合MLINEX损失函数下，θ的多层Bayes估计分别为：

证明：根据Bayes定理，则形状参数θ的多层后验密度函数为：

（1）当θ的多层先验密度函数为式（17）时，θ的多层后验密度函数为：

同理可得：

（2）同理，当θ的多层先验密度函数为式（18）时，θ的多层后验密度函数为：

结合定理1，此时形状参数θ的多层Bayes估计为：

（3）同理当θ的多层先验密度函数为式（19）时，θ的多层后验密度函数为：

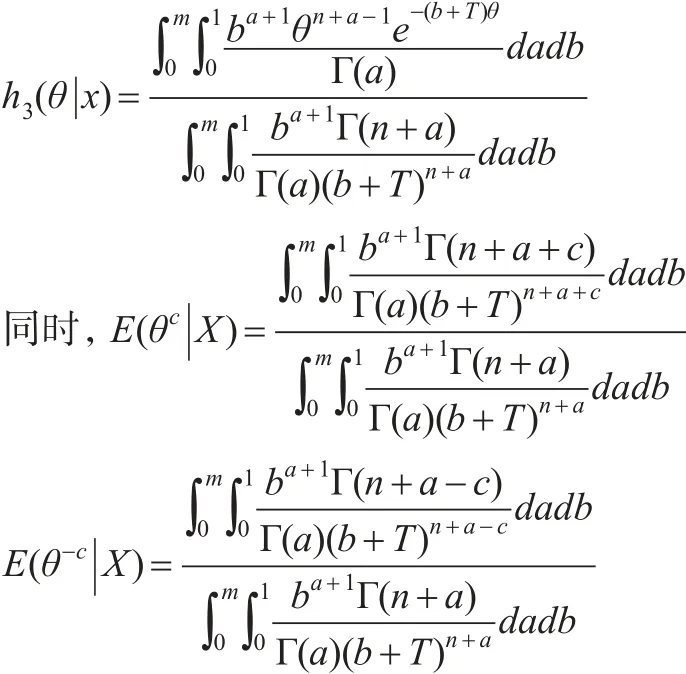
结合定理1，此时形状参数θ的多层Bayes估计为：

4　参数θ的E-Bayes估计的性质

定理5：在定理2中，当0＜m＜T时，有以下两个结论：

证明：根据定理2，有：

当-1＜x＜1时，根据泰勒展开式有：

5　结束语

本文对Pareto分布在尺度参数为已知时,在MLINEX对称损失下，分别给出了三种不同超参数的先验密度函数下形状参数E-Bayes估计（定理3）和多层Bayes估计（定理4），并验证了形状参数的三个不同E-Bayes估计具有保三者在T→∞时极限相等。

参考文献：

[1]Pareto V.Cours Economic Politique[M].Lausanne and Paris:Rouge and Cie,1897.

[2]韩慧芳,杨珂玲,张建军.Pareto分布中形状参数的估计问题[J].统计与决策,2007，(24).

[3]韦程东,韦师,苏韩.复合LINEX对称损失下Pareto分布形状参数的E-Bayes估计及应用[J].统计与决策,2009，(17).

[4]井晓培,周菊玲.广义Pareto分布参数的经验Bayes检验问题[J].数学的实践与认识,2016，(5).

[5]沈新娣,丁帮俊.Pareto分布在逐步Ⅱ型区间删失下的参数估计[J].应用概率统计,2016,32(2).

[6]韩明.Pareto分布形状参数的E-Bayes估计和多层Bayes估计及其应用[J].纯粹数学与应用数学,2016,32(3).

[7]Podder C K,Roy M K.Bayesian Estimation of the Parameter of Maxwell Distribution Under MLINEX Loss Function.[J].J.stat.stud,2003.

[8]Podder C K.Comparison of Two Risk Functions Using the Pareto Distribution[J].Pakistan Journal of Statistics,2004,20(3).

[9]任海平,李中恢.加权平方损失函数和MLINEX损失函数下一类分布族参数的Minimax估计[J].统计与决策,2009,(14).

[10]金秀岩.复合MLINEX对称损失函数下对数伽玛分布参数的Bayes估计[J].数学的实践与认识,2014,(19).

[11]张睿.复合LINEX对称损失下的参数估计[D].大连：大连理工大学硕士论文,2007.