从能量和信息理论视角理解单取代烷烃的异构化

钟爱国，李嵘嵘，洪琴，张杰，陈丹

1　lntroduction

It is widely accepted both by the experimental measurements1and high-level ab initio computations2that branchedalkanehydrocarbonsaregenerally thermodynamically more stable than its straight-chain counterpart. Nevertheless, this phenomenon is somewhat counterintuitive at first glance. In chemistry, steric effects are a consequence of the space required to accommodate the atoms and groups within a molecule, and are often thought to be predominated by repulsive forces arising from overlapping electron densities. In this sense, more branched alkanes normally engender more steric destabilization energy than the normal ones. However, we have just touched upon one side of the“coin”. Simultaneously, there exist some attracting interactions between alky groups, stemming from electron correlation. Thus, inclusion of attractive interactions such as London dispersion forces is indispensable to understand electronic and geometrical structures. Finally, these two forces coexist that makes such a phenomenon a hard nut to crack.

To provide a unified explanation for this abnormal phenomenon, a surge of interest has been aroused. Schleyer et al. pointed out that intramolecular 1,3-alkyl-alkyl interactions make positive contributions to the molecular stability of hydrocarbons3,4. Nonetheless, this“protobranching” or“prototypical branching” model was severely criticized by Gronert. He5argued that it cannot be rationalized by a through-space model of dispersive London forces. Pitzer and Catalano6have also provided an explanation for the relative stability of branched alkanes based on dispersion interactions.But this argument does not hold because the Hartree-Fock (HF)approach intrinsically has no electron correlation but is able to predict the correct stability trend3. In this regard, the overall stabilization effect does not originate from a simple physical picture.

In the literature, there are some other orbital-based intramolecular stabilization explanations. Ma and Inagaki7proposed an orbital phase rational and found that σ cross conjugation between two C―H bonds and one C―C bond in an antiperiplanar conformation in branched alkanes results in greater orbital stabilization than straight-chain σ orbital conjugation8. Kemnitz et al. employed natural bond orbital(NBO) analysis9and valence bond theory to argue that10germinal carbon-carbon σ to σ* second-order donor-acceptor orbital interactions account for the branching stability.However, this hyperconjugation model has an inherent drawback since this perturbative type of energy analysis is referenced to a hypothetical localized state that does not analyze/partition the total energy of each molecule.

The objective of this paper is two-fold. First, we aim to find out the physical differences of mono-substituted linear and branched alkanes alkane derivatives (see Fig.1 for details). It is intuitive that the isomerization from a linear to a branched alkane involves differences in steric energy. Like many concepts in chemistry, actually there is no exact definition of steric effect. Liu has proposed that the Weizäcker kinetic energy can be employed as a novel definition of steric effect in DFT11,12. This density-based quantification of the steric effect differs from its conventional wavefunction-based counterpart.The latter definition is resulted only from orthogonality and exchange antisymmetry of the wavefunction (the Fermi hole)8.This density-based steric definition is quite in accordance with the early definition by Weisskopf who ascribed the steric repulsion to “kinetic energy pressure”13. In this work, we employ two energy decomposition schemes in Kohn-Sham density functional theory (KS-DFT) to understand the total physical differences between branched and linear alkanes.Isolation of a specific intramolecular interaction is beyond the scope of this paper.

Fig.1　Schematic representations of mono-substituted alkane derivatives under study.

Second, other two density-based key quantities from information theory, Shannon entropy and Fisher information are taken into consideration at molecular level to gain insights into the transformation of mono-substituted alkane derivatives.The questions we will address are (i) whether the branched effect is always valid and (ii) what effect(s) dominantly contribute(s) to the validity of this branched effect.

This paper is mainly laid out as follows. In section 2, we outline the total energy decomposition schemes, followed by computational details. After the results and discussion in section 3, a brief summary is given in section 4.

2　Theory

2.1　An outline of the two energy partition schemes

In conventional KS-DFT, the total energy of a system, Ε[ρ],can be cast in the form of three independent contributions Ts[ρ],Εe[ρ], and Εxc[ρ] (Eq.(1))14,

where the first term Ts[ρ] signifies the non-interacting one-electron kinetic energy, the second term Εe[ρ] is the electrostatic potential, as shown in Eq.(2), a combination of the nuclear to electron attraction stabilization, Vne[ρ], the classical inter-electronCoulombicrepulsion,J[ρ],andthe nuclear-nuclear repulsion, Vnn, and the last term Εxc[ρ] is a sum of the exchange and correlation energy components.

Unlike the definition in Eq.(1), Liu12proposed a novel energy partition scheme (Eq.(3)), to unambiguously quantify the omnipresent steric repulsion, as defined by the Weizäcker kinetic energy, Tw[ρ]

with

and

where Εsand Εqare the steric effect and fermionic quantum effects, respectively. The electrostatic potential Εeis exactly the same as that defined in Eq.(2), ρ(r) is the total electron density distribution, and ∇ρ(r) is the first-order derivative. It is worth mentioning that the Weizäcker kinetic functional is the exact kinetic functional for one-electron atoms and two-electron Hartree-Fock atoms. It has become an essential ingredient in orbital-free DFT15.

This novel density-based definition of steric effect is totally different from its wavefunction-based counterpart, resulted from the Pauli Exclusion Principle that solely accounts for the electrons possessing the same spin. In this work, these two energy partition schemes will be utilized to analyze the isomerization energy between the linear and branched hydrocarbon derivatives, and its components to find out which component is the predominant term that governs the transformation of an alkane. The new scheme has recently been applied to a couple of systems16-25, among which are bond rotation barriers, cis-effect, anomeric effect, SN2 reaction barriers, water clusters, beryllium bonding interactions, and so on. A key point from these different investigations is that the electrostatic potential is the leading term while other contributions from the steric repulsion and quantum exchange-correlation interactions play minor but nontrivial roles. It is worthwhile to mention that energy partitioning scheme with Weizäcker functional (in our case Εs[ρ]) as the dominant term was shown elsewhere as well26.

2.2　Shannon entropy and Fisher information

In information theory, Shannon entropy SSis defined as the following27：

where SS(r) is the Shannon entropy density and ρ(r) is the total electron density of a molecular system, satisfying the following condition：

with Ν as the total number of electrons in the system. In addition, Fisher information, IF, is defined as follows28：

where iF(r) is the Fisher information density and ∇ρ(r) is the density gradient. To calculate the atomic values of Shannon entropy in a molecule, Eq.(11) can be recast as follows：

where

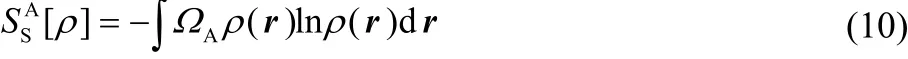
with ΩAthe atomic basin of atom A. Bader′s zero-flux partition condition is employed to partition atoms in molecules29. The same is true for Fisher information,

with

2.3　Computational details

All mono-substituted hydrocarbons CnH2n+1―R (n = 3, 4, 5,6; R = OH, OCH3, NH2, NO2, F, Cl, CN, CHO) (see Fig.1 for details) were fully optimized at the M06-2X/6-311+G(d,p)28level of theory. No symmetry constraint was imposed to allow for full variational degrees of freedom. All local minima on the hyper-potential surface were further verified by vibrational frequency calculations (e.g., no imaginary frequency). DFT total energy evaluations and steric energy decomposition calculations were carried out by employing the M06-2X functional with Dunning′s augmented correlation-consistent valence polarized triple-ζ basis set aug-cc-pVTZ (denoted as aVTZ) in NWChem 6.6,30a freely accessible computational chemistry package. Furthermore, a relatively larger basis set aug-cc-pVQZ (aVQZ), was taken into consideration to guarantee the rationalization of our results. M06-2X is superior to B3LYP31,32in many aspects, especially in the description of ubiquitousdispersionforces,irrespectiveofits“over-parameterization”. The tight self-consistent field (SCF)convergence criteria and ultrafine integration grids were employed throughout to rule out numerical problems. Suffice to note that the M06-2X functional gives isomerization energies very close to those predicted by the “gold standard” CCSD(T)in quantum chemistry and experiment.2All MP2 and CCSD(T)computations were executed with the frozen core (FC)technique to reduce the computational cost without compromising the accuracy too much. One more point to mention is that zero-point corrections were not considered in our computations. The linear alkane derivatives are taken as reference so that the isomerization energy is negative in all cases. Unless otherwise stated, all energy differences and its components are in unit of kJ·mol-1.

Additionally, we employed a multifunctional wavefunction analyzer, Multiwfn33,34to calculate the Shannon entropy and Fisher information at molecular level by utilizing the M06-2X/aVTZ molecular wavefunction as an input file in molden format. To eliminate the numeric instabilities and guarantee the rationalization of our results, we adopted 150 points in radial and 1454 points on spherical surface of Becke′s numerical quadrature.

3　Results and discussion

3.1　Validation

Table 1 exhibits the isomerization energy of a serials of mono-substitutedalkanesC3H7-Rwithboth electron-withdrawing and electron-donating groups R = OH,OCH3, NH2, NO2, F, Cl, CN, and CHO. Here we have chosen two typical density functionals M06-2X and B3LYP. It is well-established that B3LYP inherently fails to depict the dispersion forces which have a far-reaching effect on the molecular stability. In this sense, for comparison we have adopted some B3LYP variants with a portion of empirical dispersion, such as Grimme′s density-independent, atomic pair wise corrections, D3BJ (B3LYP_D3BJ),35the exchange-hole dipole moment (B3LYP_XDM)36theory proposed by Becke andJohnson,andthedispersion-core-potential(B3LYP_DCP)37model, which contains both local and semilocal terms. All the structures both reactants and products were optimized by using each method with Pople′s standard basis set 6-311+G(d,p) while all post-HF optimizations were carried out at the MP2/6-311+G(d,p) level of theory. The aVTZ basis set was employed to obtain more accurate energy differences. An even larger basis set aVQZ was employed to confirm the rationalization of the aVTZ results. The CCSD(T)/aVTZ results were taken as a reference to evaluate the overall performances of HF, MP2 and DFT B3LYP and M06-2X. Two statistical parameters, mean signed error (MSE)and mean absolute error (MAE) were adopted.

A quick inspection of Table 1 can give rise to some points in order： (i) all the methods under consideration can give a qualitative prediction of the isomerization energies (negative insign), indicating that electron correlation is not the only factor that is responsible for the relative stability of mono-substituted alkanes since HF intrinsically has no electron correlation; (ii)compared with CCSD(T), MP2 and B3LYP_DCP overestimate the isomerization energies while the rest approaches adopted[M06-2X, B3LYP, B3LYP_D3BJ, B3LYP_XDM, and HF]underestimate the data; (iii) dispersion-corrected B3LYP variants improve the energy differences to some extent, with mean absolute errors (MAEs) decreasing from 3.4 kJ·mol-1of B3LYP to 2.2 kJ·mol-1of B3LYP_D3BJ, 2.0 kJ·mol-1of B3LYP_XDM, and 2.3 kJ·mol-1of B3LYP_DCP, respectively;however, they are still far from satisfactory when compared with CCSD(T) and entail more substantial improvement; (iv)compared with the CCSD(T) data, M06-2X has the best performance if combined with the aVTZ basis set. In a nutshell,we have screened a rational and cost-efficient combination of method and basis set M06-2X/aVTZ and it will be employed for further energy decomposition analysis.

Table 1　Total energy difference (in kJ·mol-1) of the isomerization reaction of C3 serials a.

3.2　Total energy decompositions

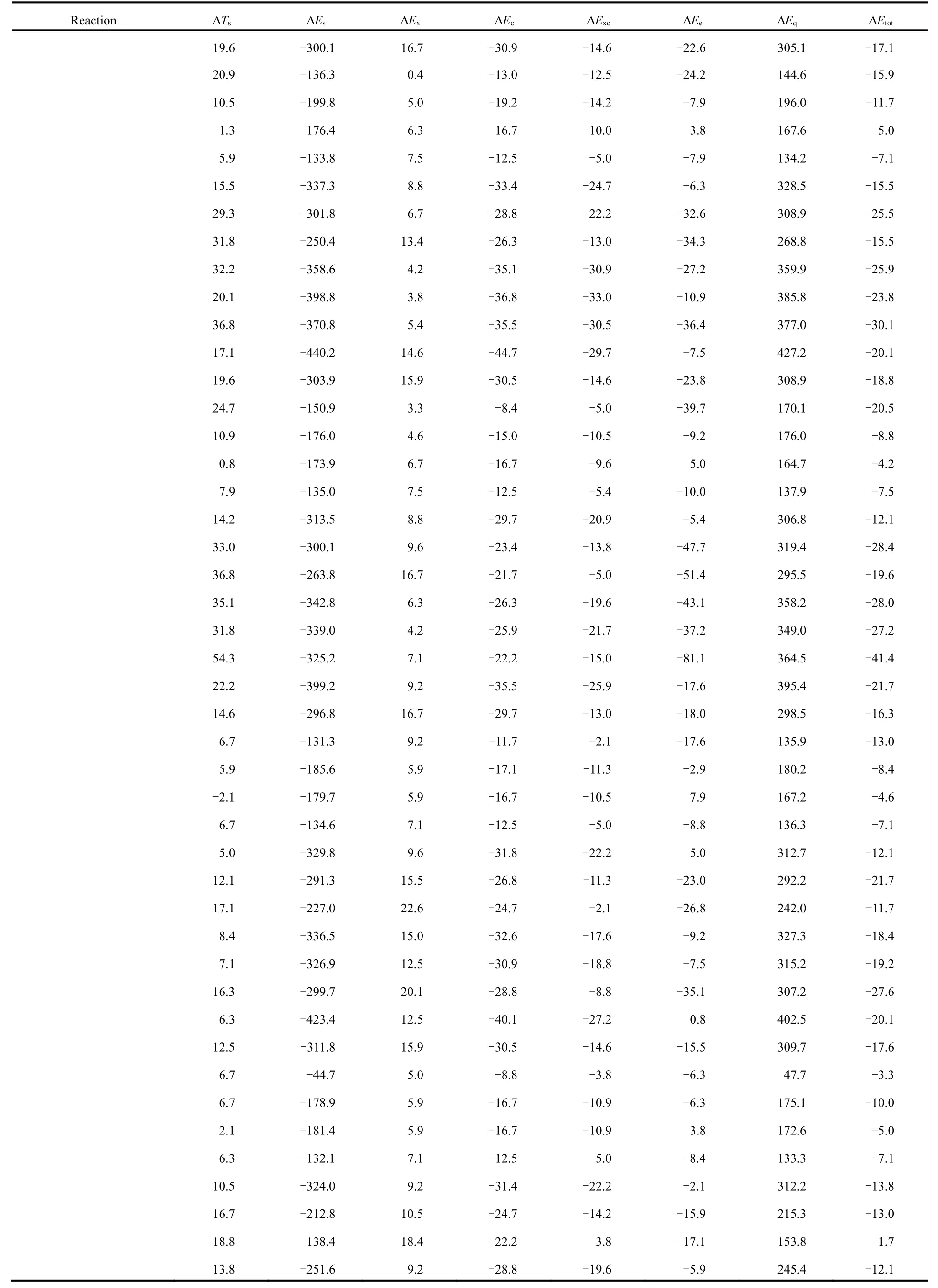
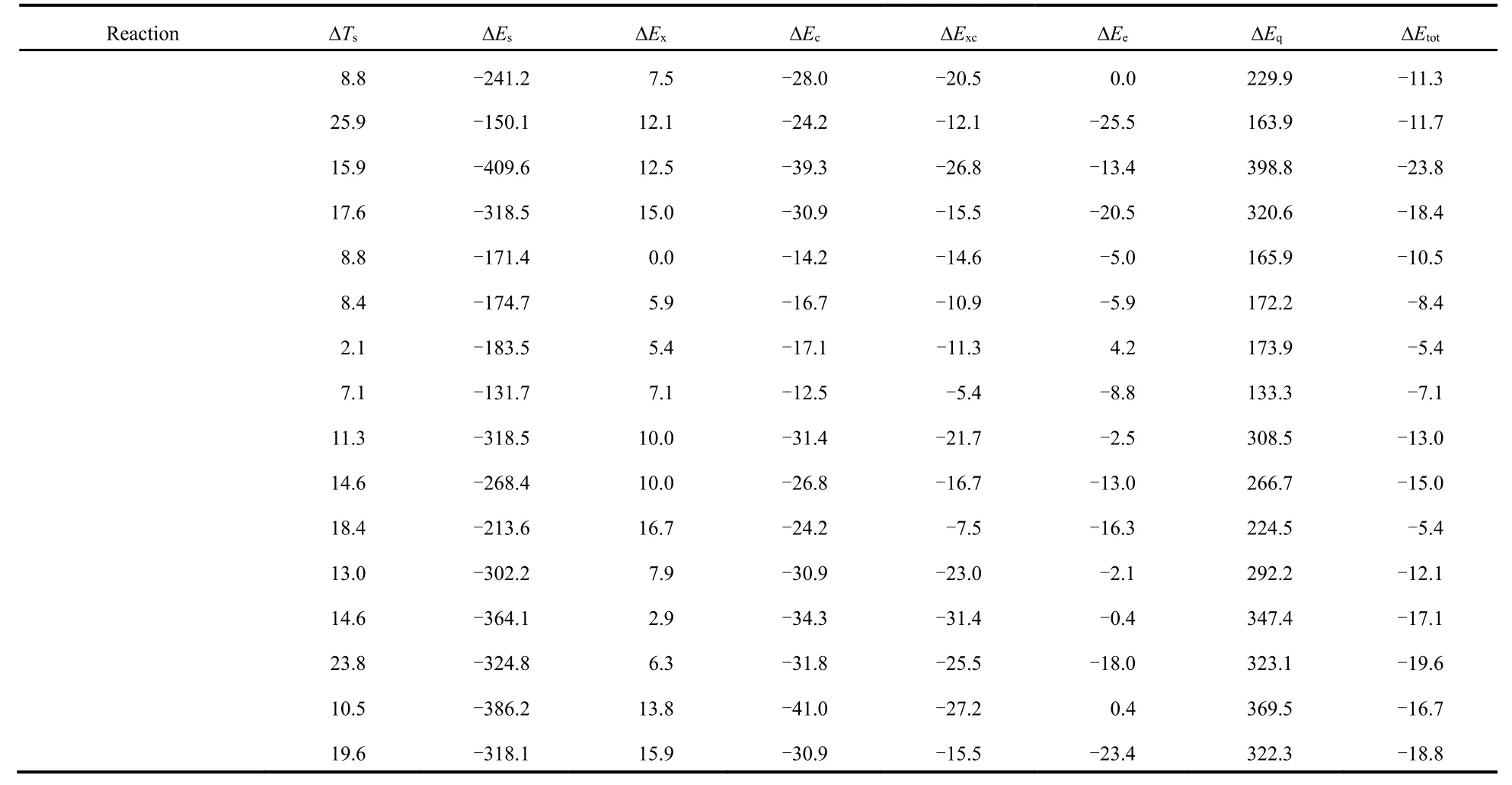
Table 2 shows the total energy difference (∆Εtot) νia the conventional and newly proposed energy partition schemes and its components： kinetic energy (∆Ts), steric hindrance (∆Εs),exchange (∆Εx), correlation (∆Εc), electrostatic potential (∆Εe)and quantum effect (∆Εq), which are obtained at the M06-2X/aVTZ level of theory, with the geometries completely optimized at the M06-2X/6-311+G(d,p) level of theory.

From Table 2, one can readily see that the total energy difference is negative in sign, indicating that the branched alkane derivatives are energetically favorable. Among all the energy components, steric potential (∆Εs) and exchangecorrelation potential (exceptions do exist in C3 serials) possess negative values, meaning that they make positive contributions to the total energy difference, while they are largely compensated by the quantum effect (∆Εq) and kinetic energy (∆Ts), respectively. An intriguing phenomenon has been discovered that for the C3 serials the exchangepotential (∆Εx) is larger than the correlation (∆Εc) in absolute values and the results are reverse for these two energy components in the rest serials. It is worthwhile to point out that only the total effect of exchange and correlation potential has a physical meaning. Meanwhile, we find that there exists a strong linear relationship between the quantum effect and steric hindrance, with the correlation coefficient R2= 0.99 (Fig.2a),serving as a confirmation of no systematic errors of our computational results. Similar trends have been observed in previous studies21-23.

Table 2　Total energy difference (∆Etot) and its components with kinetic energy (∆Ts), steric hindrance (∆Es), exchange (∆Ex), correlation (∆Ec),electrostatic potential (∆Ee) and quantum effect (∆Eq), evaluated at the M06-2X/aVTZ level a.

continued Table 2

continued Table 2

continued Table 2

continued Table 2

Furthermore, we aim to find out if there exists a single energy component that dictates the isomerization of alkane derivatives. To make that happen, in Fig.2(b, c), we have plotted the electrostatic potential (∆Εe) and the kinetic energy(∆Ts) νs the total energy difference (∆Εtot), respectively. The corresponding correlation coefficient R2is only 0.65 and 0.71 while those for the remaining energy components are less than 0.5 and ignored. In a previous work for alkanes without substituents, Εecan be linearly related to Εtot, but that's a special case21.

Fig.2　Correlations between (a) steric potential and quantum effect (y = -0.98 x + 7.63, R2 = 0.99); (b) total energy difference and electrostatic potential (y = 0.40x - 8.61, R2 = 0.64), and (c) total energy difference and kinetic energy (y = -0.68 x - 0.84, R2 = 0.71), the y axis spans from (b) to (c).

Up to now, we have revealed that no such a single energy component that governs the isomerization of alkane derivatives, which is reminiscent of the resultant force in nature for such a phenomenon. Furthermore, we want to look into the relative importance of energy components contributing the total energy, thus rendering the so-called “branching effect”. To this end, we have employed a two-variable strategy.

In Fig.3, we plotted the total energy difference νs the two components： the electrostatic potential (∆Εe) and steric hindrance (∆Εs), with R2= 0.98. Moreover, we can find out the relative significance of the two energy components νia the coefficients. It is clearly shown that the electrostatic potential plays a predominant role while the steric effect has some minor effect in the transformation of mono-substituted alkane derivatives, with the coefficients 0.33 and 0.04, respectively. In other words, though steric hindrance is engendered due to the branching of alkanes, this portion is overwhelmingly compensated by the electrostatic potential.

3.3　Shannon entropy and Fisher information

Having touched upon one side of the coin, the total energy and its components, next we will switch our gear from an information-theoreticviewpointbyanalyzingthe M06-2X/aVTZ wavefunction. Here in this work, suffice to note that our Shannon entropy and Fisher information data are based on the electron probability density, rather than the shape function. From the information theory point of view, Shannon entropy measures the spatial delocalization of the electronic density, and Fisher information measures its sharpness or concentration. They sound to be vastly different measurements but apparently in electronic systems, these two density-based quantities are not absolutely independent. They are strongly correlated to each other, as theoretically proven earlier38and numerically shown39,40. We have plotted the Shannon entropy difference and Fisher information difference in Fig.4 with the correlation coefficient R2= 0.74. Once again, we have verified that Shannon entropy and Fisher information are interrelated as a windfall of this work. The linear correlations of these two quantities can be used an evidence of weak interactions as previously shown in beryllium bonds24, though it is not observed here. We have also plotted the Shannon entropy difference νs the electrostatic potential energy difference ΔΕeor Fisher information difference νs total energy difference ΔΕtotwith the correlation coefficient R2＜ 0.20. That the total energy difference ΔΕtotdoes not strongly correlate any of these information-theoretic quantities suggests that the branched alkanes effect is of the complex nature.

Fig.3　A binary fit of total energy difference (∆Etot) with electrostatic potential (∆Ee) and steric hindrance (∆Es).

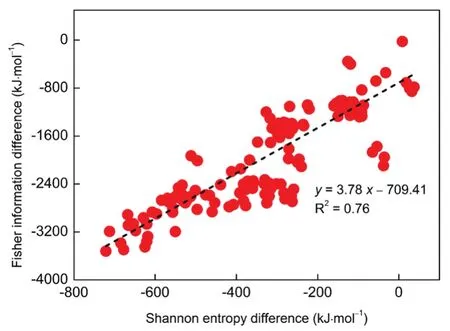
Fig.4　Linear correlation between Shannon entropy difference and Fisher information difference.

4　Concluding remarks

Isomerization of mono-substituted alkanes from energetic and information-theoretic perspectives was investigated within the KS-DFT framework. To this end, the KS-DFT total energy and a newly proposed energy partitioning scheme were employed as well as Shannon entropy and Fisher information from information theory. We have found that no such a single energy component dictates the transformation of the mono-substituted alkane derivatives. Molecular stability is governed by a resultant force. From the binary fit, we have unraveled that the electrostatic potential and the steric repulsion are responsible for the relative stability of linear and branched alkanes. Moreover, from the regression coefficient, we have shown that the electrostatic potential has played a predominant role while the steric effect has a trivial role. Shannon entropy and Fisher information at molecular level are linearly correlated, which is in line with our previous work.

(1)Olah, G. A.; Molnur, A. Hydrocarbon Chemistry; Wiley： New York,1995.

(2)Miao, J.; Hua, S.; Li, S. Chem. Phys. Lett. 2012, 541, 7.doi： 10.1016/j.cplett.2012.05.067

(3)Wodrich, M. D.; Wannere, C. S.; Mo, Y.; Jarowski, P. D.; Houk, K.N.; Schleyer, P. V. R. Chem. Εur. J. 2007, 13 (27), 7731.doi： 10.1002/chem.200700602

(4)Allen, T. L. J. Chem. Phys. 1959, 31, 1039. doi： 10.1063/1.1730501

(5)Gronert, S. Chem. Εur. J. 2009, 15 (21), 5372.doi： 10.1002/chem.200800282

(6)Pitzer, K. S.; Catalano, E. J. Am. Chem. Soc. 1956, 78, 4844.doi： 10.1021/ja01600a006

(7)Ma, J.; Inagaki, S. J. Am. Chem. Soc. 2001, 123, 1193.doi： 10.1021/ja003067v

(9)Badenhoop, J. K.; Weinhold, F. J. Chem. Phys. 1997, 107 (14), 5406.doi： 10.1063/1.475149

(10)Kemnitz, C. R.; Mackey, J. L.; Loewen, M. J.; Hargrove, J.L.; Lewis, J. L.; Hawkins, W. E.; Nielsen, A. F. Chem. Εur. J.2010, 16 (23), 6942. doi： 10.1002/chem.200902550

(11)Weizsäcker, C. F. V. Z. Phys. 1935, 96, 431.doi： 10.1007/BF01337700

(12)Liu, S. B. J. Chem. Phys. 2007, 126, 244103.doi： 10.1063/1.2741244

(14)Parr, R. G.; Yang, W. Density Functional Theory of Atoms and Molecules; Oxford University Press： Oxford, 1989.

(15)Chakraborty, D.; Kar, S.; Chattaraj, P. K. Phys. Chem. Chem.Phys. 2015, 17, 31516. doi： 10.1039/C5CP00995B

(16)Liu, S. B.; Govind, N. J. Phys. Chem. A 2008, 112 (29), 6690.doi： 10.1021/jp800376a

(17)Liu, S. B.; Govind, N; Pedersen, L.G. J. Chem. Phys. 2008,129 (9), 094104. doi： 10.1063/1.2976767

(18)Uğur, İ.; Vleeschouwer, F. D.; Tüzün, N.; Aviyente, V.;Geerlings, P.; Liu, S. B.; Ayers, P. W.; DeProft, F. J. Phys.Chem. A 2009, 113 (30), 8704. doi： 10.1021/jp903371b

(19)Torrent-Sucarrat, M.; Liu, S. B.; DeProft, F. J. Phys. Chem. A 2009, 113 (15), 3698. doi： 10.1021/jp8096583

(20)Liu, S. B.; Hu, H.; Pedersen, L. G. J. Phys. Chem. A 2010,114, 5913. doi：10.1021/jp101329f

(21)Tsirelson, V. G.; Stash, A. I.; Liu, S. B. J. Chem. Phys. 2010,133 (11), 114110. doi： 10.1063/1.3492377

(22)Ess, D. H.; Liu, S. B.; DeProft, F. J. Phys. Chem. A 2010, 114,12952. doi： 10.1021/jp108577g

(23)Zhao, D. B.; Rong, C. Y.; Jenkins, S.; Kirk, R. S.; Yin, D. L.;Liu, S. B. Acta Phys. -Chim. Sin. 2013, 29 (1), 43. [赵东波,荣春英, 苏曼, 苏文, 尹笃林, 刘述斌. 物理化学学报,2013, 29 (1), 43.] doi： 10.3866/PKU.WHXB201211121

(24)Wang, Y. J.; Zhao, D. B.; Rong, C. Y.; Liu, S. B. Acta Phys. -Chim.Sin. 2013, 29 (10), 2173. [王友娟, 赵东波, 荣春英, 刘述斌. 物理化学学报, 2013, 29 (10), 2173.]doi： 10.3866/PKU.WHXB201308272

(25)Zhong, A. G.; Chen, D.; Li, R. R. Chem. Phys. Lett. 2015,633, 265. doi： 10.1016/j.cplett.2015.06.007

(26)Deb, B. M; Chattaraj, P. K. Phys. Reν. A 1989, 39, 1696.doi： 10.1103/PhysRevA.39.1696

(27)Shannon, C. E. Bell Syst. Tech. J. 1948, 27, 379.doi： 10.1002/bltj.1948.27.issue-3

(28)Fisher, R. A. Proc. Camb. Philos. Soc. 1925, 22, 700.doi： 10.1017/S0305004100009580

(29)Bader, R. F. W. Atoms in Molecules： A Quantum Theory;Oxford University Press： Oxford, 1990.

(30)Zhao, Y.; Truhlar, D. G. Theor. Chem. Acc. 2008, 120, 215.doi： 10.1007/s00214-007-0310-x

(31)Valiev, M.; Bylaska, E. J.; Govind, N.; Kowalski, K.;Straatsma,T. P.; van Dam, H. J. J.; Wang, D.; Nieplocha, J.;Apra, E.; Windus, T. L.; et al. Comput. Phys. Commun. 2010,181, 1477. doi： 10.1016/j.cpc.2010.04.018

(32)Becke, A. D. J. Chem. Phys. 1993, 98, 1372.doi： 10.1063/1.464304

(33)Lee, C.; Yang, W.; Parr, R. G. Phys. Reν. B 1988, 37, 785.doi： 10.1103/PhysRevB.37.785

(34)Lu, T.; Chen, F. J. Comput. Chem. 2012, 33 (5), 580.doi： 10.1002/jcc.22885

(35)Lu, T. Multiwfn, Version 3.3; A Multifunctional Wavefunction Analyzer, 2016, http：//multiwfn.codeplex.com (accessed Sep 18, 2016).

(36)Grimme, S.; Ehrlich, S.; Goerigk, L. J. Comput. Chem. 2011,32, 1456. doi： 10.1002/jcc.21759

(37)Becke, A. D.; Johnson, E. R. J. Chem. Phys. 2005, 122,154104. doi： 10.1021/acs.chemrev.5b00533

(38)Heßelmann, A. J. Chem. Phys. 2009, 130 (8), 084104.doi： 10.1063/1.3077939

(39)Liu, S. B. J. Chem. Phys. 2007, 126, 191107.doi： 10.1063/1.2741244

(40)Rong, C. Y.; Lu, T.; Liu, S. B. J. Chem. Phys. 2014, 140 (2),024109. doi： 10.1063/1.4860969