BP神经网络隐含层节点数确定方法研究

王嵘冰，徐红艳，李 波，冯 勇

(辽宁大学 信息学院，辽宁 沈阳 110036)

0 引 言

人工神经网络具有自学习、自组织和优良的非线性逼近能力，因此众多领域的学者都在对其进行研究和应用。在实际应用中，其中一种人工神经网络—BP神经网络(back propagation neural networks，BPNN)最为人们熟知，并广泛应用于人工智能、图像处理、优化算法、数据挖掘等重要领域。

在对BPNN进行深入研究的过程中，学者们提出了一个非常重要的、不可忽略的问题，即BPNN隐含层节点数确定问题。由于对神经网络隐含层节点数的确定缺乏有效的方法，目前仅能凭经验和不断地实验来确定隐含层节点数。针对这个问题，文中提出了一种行之有效的算法，即“三分法”算法。该算法可以简单、快速地确定BPNN隐含层节点数。

1 相关研究

1.1 BPNN

1986年，Rumelhart等提出了误差反向传播法，即BP算法[1]。BPNN能够实现M-N维的映射关系，而无需事先知道映射关系的数学方程式。BPNN模型由三部分构成：输入层、隐含层以及输出层[2]，模型图如图1所示。

图1为三层前馈神经网络，不含Input层，整个网络含有两个隐含层Hidden1和Hidden2，一个输出层Output，各层之间是全连接的关系。

图1 三层BPNN

BPNN实现了M维到N维的一个非线性映射关系，它包括两个过程，一是前向传播过程，二是误差反向传播过程。

当一个模式从输入端输入网络之后，这个模式将在BPNN中流动，模式通过权值线路进入每一个隐含层神经元节点，利用激活函数，隐含层各个神经元对其进行加权求和处理，之后经过隐含层和输出层之间的权值线路进入输出层单元，处理后在输出层产生一个输出模式。在输入模式转换成输出模式的期间，从输入层到输出层逐步更新各层状态的过程即前向传播过程。接着计算输出模式和期望模式的误差，如果误差大于设定的精度阈值，将误差顺着来路逐层进行反向传播，接着更新网络权值。迭代前向传播和误差反向传播这两个过程，直至所有训练样本的误差平方和都满足精度要求为止，至此BPNN的整个学习过程就完成了。

1.2 影响BPNN性能的参数

为了设计合理的BPNN，有必要探讨影响BPNN性能的参数，影响BPNN性能的参数如下：

(1)隐含层数：隐含层数的增加可以降低网络误差，提高精度，但同时也会使网络复杂性增大，导致网络的训练时间被增大和出现“过拟合”倾向的可能性也被增大。

(2)隐含层节点数：在BPNN中，隐含层节点数是一个非常重要的参数，它的设置对BPNN的性能影响很大，而且是“过拟合”现象的直接原因。但遗憾的是，目前理论上还不存在一种科学普遍的确定方法。这个问题将是文中关注的重点。

(3)网络的初始连接权值：BP算法的先天设计不可避免地使误差函数会有多个局部极小点存在，网络初始连接权值不同，可能导致BP算法收敛的结果不同，而这个结果不能确定是全局最优解，有可能是局部最优。

(4)学习率：网络训练时，网络学习的稳定性受到学习率的影响。设定的学习率大，网络学习速度快，但会导致修正权值时权值会呈现不规则跳跃而无法收敛；设定的学习率小，网络学习速度慢，可能使网络收敛于某个极小值，缺点是会导致学习时间过长。

(5)动量系数：为解决易收敛到极小值、训练时间长等缺陷，引入了动量系数因子[3]。附加动量项能够使得权值的调整趋于平滑稳定，易找到全局最小值[4]。

2 BPNN与隐含层节点数

2.1 隐含层节点数对BPNN的影响

在BPNN中，隐含层节点数是一个非常重要的参数，它的设置对BPNN的性能影响很大[5]，而且是“过拟合”现象的直接原因，目前理论上还没有一种科学的方法可以确定隐含层节点数。由于输入输出层节点数，以及问题的复杂度和转换函数等都可能影响隐含层节点数的确定，它的确定有了更多的不确定性。

若隐含层节点数太少，那么会使得网络无法学习；若太多，虽然在一定程度上可以减小系统误差，但无疑会增加网络学习的时间，而且会使训练掉入局部极小点的陷阱，这也是“过拟合”的内在原因。因此，如何合理设计隐含层节点数，是一个不可避免的问题。确定隐含层节点数可以遵循一条基本原则，尽可能取较少的节点数来满足问题的精度要求。

对非训练样本的支持能力称为网络泛化能力[6]。而泛化能力与网络的结构，即隐含层数和隐含层节点数有关[7]。学者Nielson通过理论证明存在一个BPNN，只有一个隐含层，但能够逼近在闭区间连续的任何函数[8]，因此不用考虑隐含层层数问题。

2.2 传统隐含层节点数的确定方法

隐含层节点数的选择是个十分复杂的问题，需要设计者有着长期的实践积累，凭借自己以往的经验以及借助多次实验进行确定。隐含层节点数与问题的需求、输入输出单元的数目有着不可割舍的直接关系。若数目太少，则BPNN不能获取足够的信息用来解决问题需求；若数目太多，会增加学习时间，还会使学习时间过长，却不能保证最终结果最好，同时可能出现“过拟合”问题。文献[9]说明最佳的隐层节点数一定存在，如何寻找得到这个最佳节点数是一个值得思考的问题。针对该问题，许多学者给出了各种解决方案[10-13]，也提出了不少经验公式。

(1)

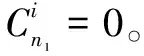
n1=(n+m)1/2+a

(2)

其中，n为输入层节点数；m为输出层节点数；a为1～10之间的常数。

n1=log2n

(3)

解决方案总结起来有以下几类：

(1)实验法，这是一种最无奈的方法，而且消耗大量的人力；

(2)将解空间限制到某个区间内，在这个解空间中进行暴力破解，虽然简单，但消耗时间；

(3)引入超平面、动态全参数自调整等概念，这些都使得算法过于复杂，甚至超过了BPNN学习算法的复杂度，运行这些算法需要消耗过长的时间，所以需要思考一种简单有效的算法。

通过联立式1～3并求解，可以得到一个关于隐含层节点数的区间[a,b]。这个区间意味着最佳隐含层节点数所在的一个区间，只要在这个区间中寻找，就可以找到它。

第一种方法，最简单也是最容易想到的，即可以使用暴力破解的思想。所谓的暴力破解法，就是利用整个解空间中的每一个解进行验证计算。

将[a,b]之内的所有可能解代入BPNN，然后每一个解构成一个BPNN，将所有的样本通过这些神经网络进行训练，从而得到这些BPNN中最小的误差值，所对应的隐含层节点数即为所求[14]。

暴力破解法由于搜索了整个解空间，因此该算法一定是有效的，但对于时间复杂度而言，当这个区间很小或者测试样本量很小时，暴力破解算法的时间是可以接受的，但当这个区间特别大或者测试样本量很大时，所耗费的时间就可能无法容忍，需要继续改进。

暴力破解法时间消耗过长主要是因为搜索了整个解空间，如果能够在求解的过程中缩小解空间，那么时间消耗就可以减少，从而优化暴力破解算法。

3 改进的隐含层节点数确定方法

3.1 “三分法”算法思想

二分法查找是在一个有序的数组中进行折半查找，从而将查找算法的时间复杂度降到了O(log2n)。文中借鉴了二分法查找算法思想，但是考虑由于隐含层节点数和误差的关系的特殊性，不能照搬二分法，需要设计为三分法。

图2 抛物线曲线

该算法可以一次性去除2/3的不符合选项。如图2所示的抛物线中，只利用函数值如何查找最低点的位置。

第一种方法可以使用暴力破解。

(4)

当最低点位于区间内时，那么最低点所在的区间的斜率绝对值最小(图2中为区间[c,d])，且左边区间的斜率为负，右边的区间为正。所以要找到最小点，只需从[c,d]之间查找。然后在[c,d]中迭代使用“三分法”，直到[a,b]区间长度小于等于4(不能构成三个斜率)，此时只需依次比较这四个节点就可以找到最低点。

通过上述可知，三分法的适用范围为区间存在最优解，且误差模型近似为抛物线。通过式1～3获得区间内一定包含了最优的隐含层节点数，并且也可知它符合抛物线模型。

研究区间很大时，如果忽略一些特殊点形成的“突刺”(一些特殊的点上误差可能会高于理想的误差而出现波动，即突刺)，那么误差的模型是一个抛物线模型。抛物线模型最低谷是误差最小点，也就是最佳的隐含层节点数；从这个点往两侧延伸，随着远离这个平衡点，那么误差会逐渐增大。当隐含层节点数为1时，可以认为这个网络是无用的；当隐含层节点数是一个正的无穷时，网络中的冗余知识使得网络也是不可用的。

至此，可知“三分法”的实质就是将区间[a,b]分成三段，然后研究这三段的变化趋势，从而预测最优的隐含层节点数存在于哪个区间之内。斜率代表了曲线的变化趋势，斜率越小，说明变化趋势越小，也就说明了隐含层节点数就隐藏在这里。

3.2 算法合理性验证

为了说明算法的合理性，并且为了演示算法的运行步骤，在此先简要利用其他研究者的实验成果进行简单验证，后面会继续利用实验验证“三分法”算法的合理性。

在文献[15]中，有一章节研究了隐含层节点数和误差的关系，这篇论文是关于BPNN对产品质量合格率预测的研究，其实验结果如图3所示。

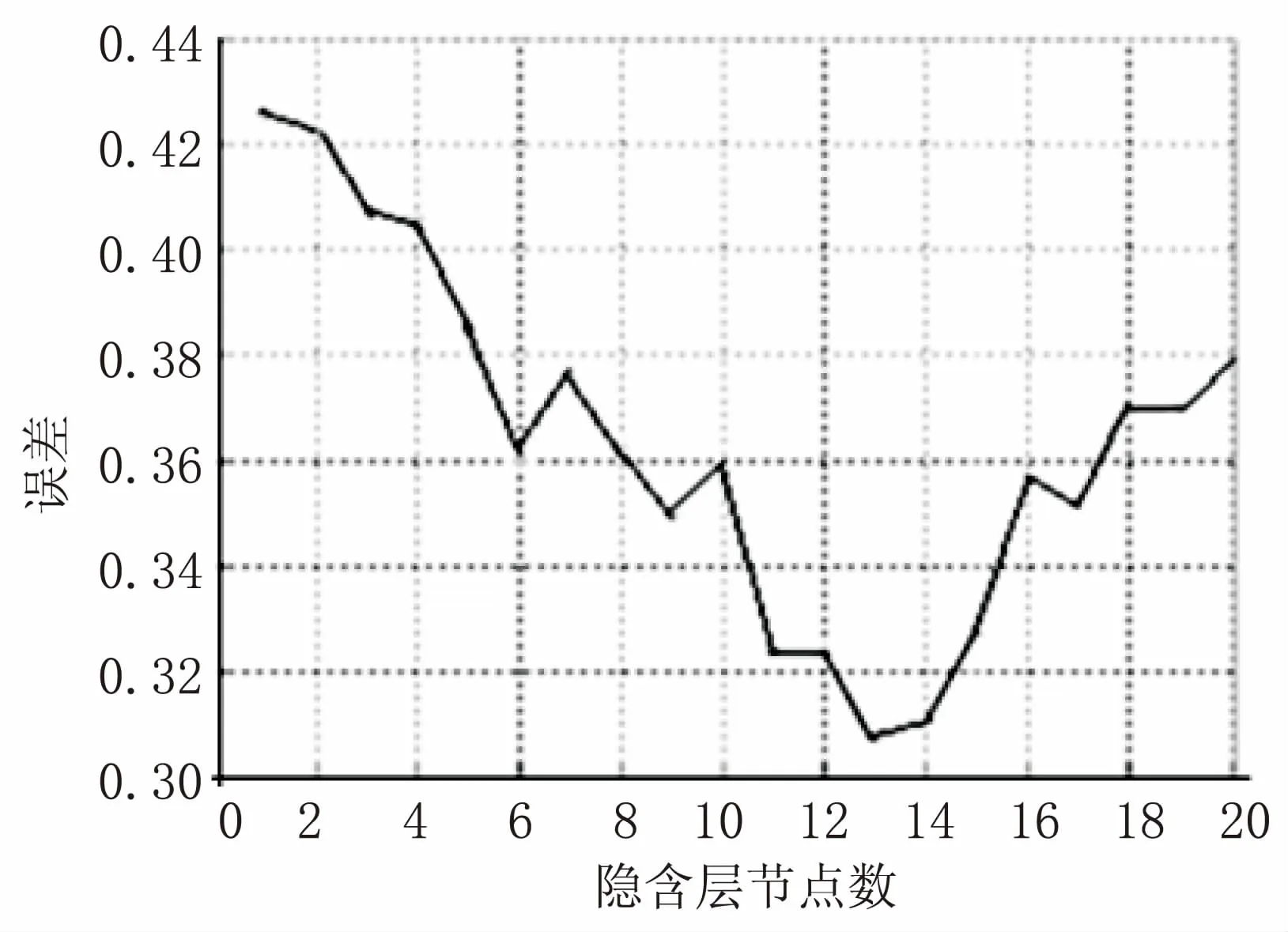
图3 隐含层和误差的关系曲线

通过观察图3可知，这是一个不规则的抛物线模型，某些地方呈不规则无规律变化，而在整体变化趋势上却呈抛物线变化，支持了上文的研究理论。对于这个关系图，如果使用暴力破解，即依次验证1～20个节点，那么需要训练20次，才能确定节点数最优解为13；如果使用三分法，那么很快就确定到节点数为6～13个。

接下来，探讨BP网络隐含层节点数确定步骤。设ki,j表示区间(i,j)的斜率，比如k1,6表示区间(1,6)的斜率。

第一步：因为k1,6<0&&k13,20>0,说明在区间(1,6)误差在下降，在区间(13,20)误差在上升，那么说明最优解可能在区间(7,12)，所以可取区间(7,12)，继续使用三分法。

第二步：因为k7,8<0&&k9,10<0&&k11,12<0，说明误差一直在下降，则可选取区间(11,12)，如此再比较隐含层节点数11和隐含层节点数12。

第三步：检测所求解的两侧的两个点就可以定位到13。

如此只需训练11次就可找到最优解，比正常的快了几乎一倍。接下来，仔细分析“三分法”算法思想。

实际上三个区间的方向性共有8种变化。设三个区间的斜率分别为k1,k2,k3，则这三个斜率的变化趋势可以分为6种情况。

(1)k1<0&&k2>0&&k3<0。

k1<0说明误差在下降，k2>0说明误差在上升，k3<0说明误差在下降，出现这种现象可以认为误差出现了“跳跃”，因此不能使用“三分法”，而使用普通的暴力破解法效果会更好。

(2)k1<0&&k2>0&&k3>0。

k1<0说明误差在下降，k2>0说明误差在上升，k3>0说明误差在上升，所以可以确定最优解在中间段区间，即使在第一段区间的末尾，由于算法会加一个调节因子，依然可以找到。

(3)k1<0&&k2<0&&k3>0。

该情形与情形(2)类似。误差变化是第一段区间下降，第二段区间下降，第三段区间上升，所以依然选择中间段区间。

(4)k1<0&&k2<0&&k3<0。

三者全都小于0，说明误差一直在下降，所以选择第三段区间。

(5)k1>0&&k2>0&&k3>0。

三者均大于0，说明误差一直在上升，所以选择第一段区间。

(6)其他情况，可以认为区间震荡，无法确定最优解会出现在哪个区间，需要使用暴力破解法。

由于算法利用的是区间的变化趋势，所以每一段区间最少为三个点，三个区间则最少需要七个点。因此设置7为临界值，当区间大小大于等于7时，一律使用暴力破解法。

其次，对于每一种情况，最优解有可能在某个区间的端点出现，这样的话有可能会错过这个解，因此为了防止最优解在区间端点出现，加入调节因子m,n。

3.3 “三分法”算法描述

在前面详细论述了“三分法”算法的求解原理和算法思想，该算法有效且简单。引入BPNN中，首先构建BPNN，利用求得的节点数区间，代入隐含层构建对应的BPNN，BPNN构建完成后，将训练样本依次通过BPNN进行训练，利用测试样本测试网络，这样最终会得到BPNN的误差和隐含层节点数的关系。

“三分法”算法流程：

(1)根据经验公式1～3确定a,b；

(2)如果b-a小于7，跳转到(8)，否则继续执行；

(3)计算c,d，并获取ka,c,kc,d,kd,b；

(4)如果ka,c<0&&kc,d<0&&kd,b<0，则a=b，跳转到(2)；否则继续向下执行；

(5)如果ka,c>0&&kc,d>0&&kd,b>0，则b=c，跳转到(2)；否则继续向下执行；

(6)如果ka,c<0&&kc,d>0&&kd,b>0，则a=c,b=d，跳转到(2)；否则继续向下执行；

(7)如果ka,c<0&&kc,d<0&&kd,b>0，则a=c,b=d，跳转到(2)；否则跳转到(8)；

(8)添加调节因子a=a-m，b=b+n，若a小于等于0，重置为1；

(9)暴力求解。

4 实验结果与分析

4.1 实验环境

文中采用Java编程技术，使用的开发工具包是jdk1.7，集成开发环境采用Eclipse，它可以很好地支持Java应用程序编程。Matlab是一种很强大的工具，集成了计算、可视化和程序设计等功能，有多种工具箱，其中包括神经网络工具箱。神经网络工具箱包括不同神经网络模型的网络学习和训练函数，其中就有BPNN，包括BPNN的新建、训练、测试，为BPNN的仿真实验提供了便利。

4.2 隐含层节点数确定实验

为了验证“三分法”算法的正确性，需要进行两部分实验。首先需要验证BPNN误差和隐含层节点数的关系，其次需要进行“三分法”算法的验证。

实验采用UCI上的数据集Wine-data，对三个不同品种的葡萄酒分别进行化学分析，从中分析出主要成分并记录该值。该数据集的任务就是实现数据分类，从而区分其所属品种。

实验获取到的结果如图4所示。

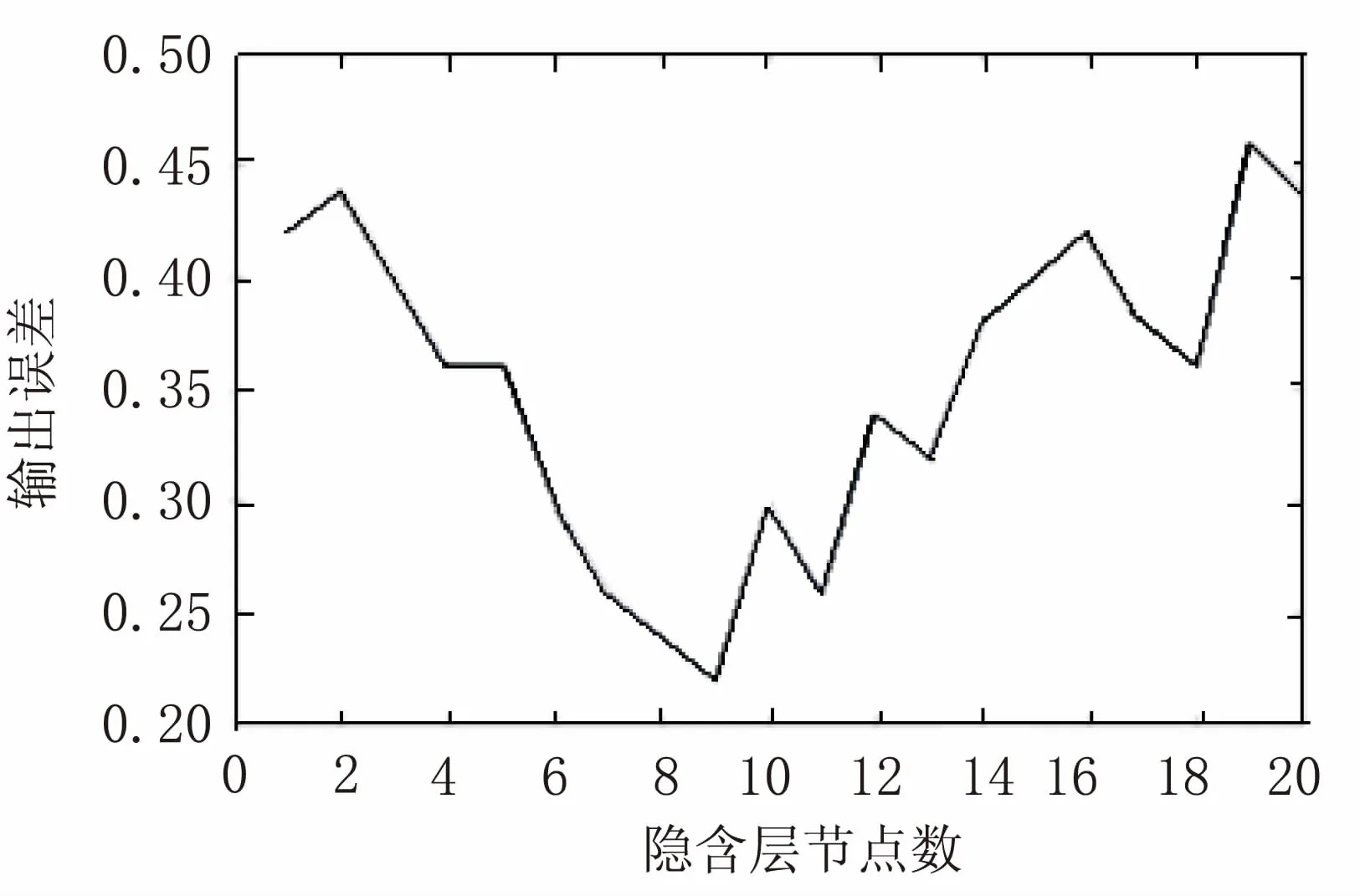
图4 网络误差与隐含层节点数的关系

通过对Wine-data数据集的实验，发现隐含层节点数与误差的关系基本符合抛物线的形式，证明了“三分法”算法的基础是有效的。而通过对这组实验结果使用“三分法”算法，最终可以获取到最佳解。程序运行过程中a，b，c，d(m,n均设置为0)变化是：

(1)a=1，c=7，d=13，b=20；

(2)a=7，c=9，d=11，b=13；

(3)a=9，b=11。

传统确定隐含层节点数的方法，需要实验节点数为1～20共20次的实验，而新的“三分法”算法实验只需要进行1，7，9，10，11，13，20共7次实验，速度提高了1.8倍，证明了“三分法”算法相对于传统方法有了明显的改进。

5 结束语

针对BPNN结构难以确定的问题，提出了“三分法”算法。通过参考相关文献、研究已有成果，发现BPNN的误差和隐含层节点数的关系基本符合抛物线模型，所以可以通过研究误差的趋势，很快定位到最优解的位置，这是“三分法”算法的基础。同时，为了解决不符合抛物线模型的情况，增强“三分法”算法的鲁棒性，结合了暴力破解法。通过示例演算可知，“三分法”算法可以快速、有效地确定隐含层节点数，是一种行之有效的算法。

参考文献：

[1] RUMELHART D E.Learning representation by back-propagating errors[J].Nature,1986,323(6088):533-536.

[2] 周启超.BP算法改进及在软件成本估算中的应用[J].计算机技术与发展,2016,26(2):195-198.

[3] 师 黎,陈铁军.智能控制理论及应用[M].北京:清华大学出版社,2009:104-105.

[4] 王晶晶,王 剑.一种BP神经网络改进算法研究[J].软件导刊,2015,14(3):52-53.

[5] BAHADIR E.Prediction of prospective mathematics teachers' academic success in entering graduate education by using back-propagation neural network[J].Journal of Education and Training Studies,2016,4(5):113-122.

[6] 周冬冬.BP神经网络样本数据预处理应用研究[D].重庆:重庆大学,2011.

[7] 李武林,郝玉洁.BP网络隐节点数与计算复杂度的关系[J].成都信息工程学院学报,2006,21(1):70-73.

[8] AZGHADI S M R,BONYADI M R,SHAHHOSSEINI H.Gender classification based on feed forward back propagation neural network[C]//International conference on artificial intelligence & innovations:from theory to applications.[s.l.]:[s.n.],2007:299-304.

[9] RASTEGAR R,HARIRI A.A step forward in studying the compact genetic algorithm[J].Evolutionary Computation,2006,14(3):277-289.

[10] 沈花玉,王兆霞,高成耀,等.BP神经网络隐含层单元数的确定[J].天津理工大学学报,2008,24(5):13-15.

[11] 张德贤.前向神经网络合理隐含层结点个数估计[J].计算机工程与应用,2003,39(5):21-23.

[12] 夏克文,李昌彪,沈钧毅.前向神经网络隐含层节点数的一种优化算法[J].计算机科学,2005,32(10):143-145.

[13] 田国钰,黄海洋.神经网络中隐含层的确定[J].信息技术,2010(10):79-81.

[14] KHANLOU H M,SADOLLAH A,ANG B C,et al.Prediction and optimization of electrospinning parameters for polymethyl methacrylate nanofiber fabrication using response surface methodology and artificial neural networks[J].Neural Computing and Applications,2014,25:767-777.

[15] 温 文.基于改进BP神经网络的产品质量合格率预测研究[D].广州:华南理工大学,2014.