盘点坐标系与参数方程模块最值问题的求解方法

卜大海

(广东省汕头市澄海苏北中学 515829)

坐标系与参数方程模块是新课标高考的选做考点，而最值问题又是该模块的高频考点，对于新加入新课标高考省份的师生来说，其命题形式和考试风格与以往自主命题时大不相同.本文总结了坐标系与参数方程模块最值问题的常见求解方法，希望对广大备考的师生有所启发和帮助.

一、应用曲线的参数方程进行三角换元求最值

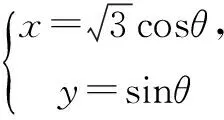
(1)写出C1的普通方程和C2的直角坐标方程；

(2)设点P在C1上，点Q在C2上，求|PQ|的最小值及此时P的直角坐标.

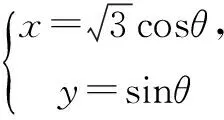
评注本题是2016年新课标丙卷第23题，破解此题关键在于利用点P参数形式的直角坐标将解析几何的最值问题转化为三角函数的最值问题.

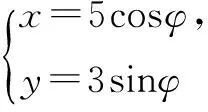
(2)求椭圆C的内接矩形ABCD面积的最大值.

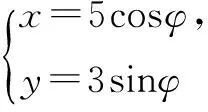
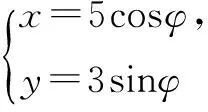
故椭圆C的内接矩形ABCD面积的最大值为30.

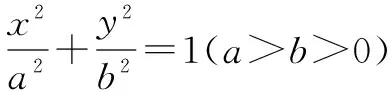
二、化归为二次函数，运用二次函数的特性求最值

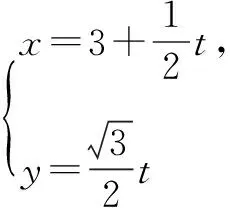
(1)写出圆C的直角坐标方程；

(2)P为直线l上一动点，当P到圆心C的距离最小时，求P的直角坐标．

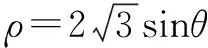
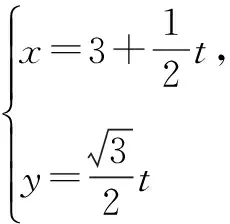
故当t=0时，|PC|取最小值，此时P点的直角坐标为(3,0).

评注题目中说P为直线l上一动点，动点从何而得？本题告诉我们一个重要的解题经验——需要动点坐标时我们可以向曲线的参数方程“借”.

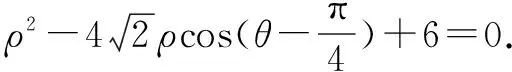
(1)求圆C的普通方程和参数方程；

(2)已知圆C上一动点P(x,y)，求xy的最大值和最小值.

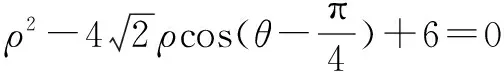
x2+y2-4x-4y+6=0，即(x-2)2+(y-2)2=2.

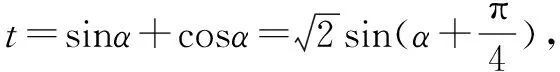
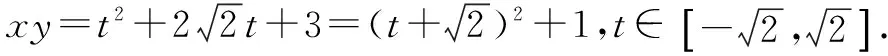
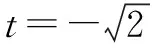
评注第二问为什么会想到将此题化为二次函数求最值呢？事实上是因为“幂次”暴露了本题的求解思路，题目中的sinα+cosα是1次幂，而sinαcosα是2次幂，具有典型二次函数结构，本题也给我们提供了一条换元经验和一个解题技巧.

换元经验：遇到含有sinα±cosα和sinαcosα的函数通常作如下换元：

解题技巧：三角函数求最值用什么方法，要看幂次说话，例如，y=cos2x+sinxcosx各项幂次均相同，可降幂结合引入辅助角公式化为三角函数最值问题，而y=cos2x+sinx这类含有2次幂，1次幂的函数，则化为二次函数求最值.

三、运用圆的几何对称特性求最值

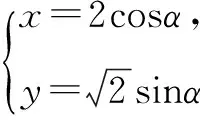
(1)求曲线C2的直角坐标方程；

(2)若P,Q分别是曲线C1和C2上的任意一点，求|PQ|的最小值.

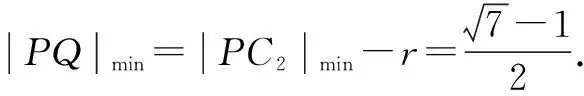
评注本题不仅用到了前面提到二次函数求最值，而且还使用了几何对称思想，即利用圆的对称性求最值.运用圆的几何对称特性求取值范围时常用到以下结论：

结论一：已知圆O的半径为r，圆O上一点到与其相离的直线l的距离为d，圆心到该直线的距离为d0，则dmax=d0+r，dmin=d0-r.

结论二：已知圆O的半径为r，圆上一点到圆外一点A的距离为d，圆心到点A的距离为d0，则dmax=d0+r，dmin=d0-r.

结论三：设圆A上一点到圆B上一点的距离为d，两圆半径分别为r1,r2，两圆圆心之间的距离为d0，若两圆相离，则dmax=d0+r1+r2，dmin=d0-r1-r2.

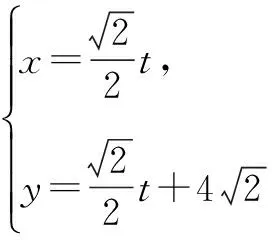
(1)求圆心C的直角坐标；

(2)由直线l上的点向圆C引切线，求切线长的最小值．

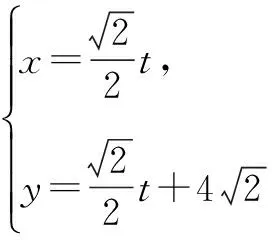
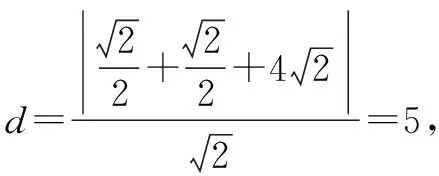
评注圆的几何最值问题围绕“圆心”思考，往往会让问题柳暗花明.本题第二问直接求解很难入手，若考虑直线l上的点到圆心的距离的最小值，则问题迎刃而解.

四、利用基本不等式求最值

例7 在极坐标系中，已知曲线C1：ρ=2cosθ和曲线C2：ρcosθ=3，以极点O为坐标原点，极轴为x轴非负半轴建立平面直角坐标系.

(1)求曲线C1和曲线C2的直角坐标方程；

(2)若点P是曲线C1上一动点，过点P作线段OP的垂线交曲线C2于点Q，求线段PQ长度的最小值.

解析(1)C1的直角坐标方程为(x-1)2+y2=1，C2的直角坐标方程为x=3，

(2)设曲线C1与x轴异于原点的交点为A,由PQ⊥OP,可知PQ过点A(2,0),

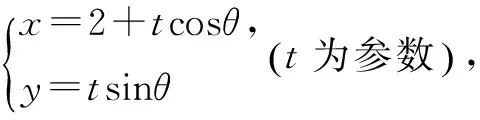
代入C1可得t2+2tcosθ=0,解得t1=0或t2=-2cosθ.

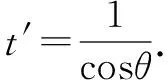
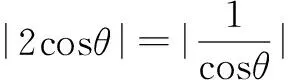
评注本题的解题关键在于设出直线PQ的参数方程及利用数形结合的思想得到|PQ|=|AP|+|AQ|，那么再面对基本不等式得最值就信手拈来了.

参考文献：

[1]张文玫.例谈高中选修4-4参数方程的应用[J].语数外学习(高中数学教学),2014(11):61-61.

[2]吴伟泉等.数学选修4-4坐标系与参数方程[M].北京：人民教育出版社，2005.