裂纹问题的一致性高阶无网格法

， ， ，

(大连理工大学 工业装备结构分析国家重点实验室，工程力学系，大连 116024)

1 引 言

裂纹扩展是很多工程结构破坏失效的主要形式之一。对该过程实施有效的数值模拟与分析是研究断裂机理乃至防止断裂破坏事故发生的主要手段之一。目前，Belytschko等[1,2]提出的扩展有限元法是模拟裂纹扩展的主要方法之一。该方法在有限元法的基础上，通过向位移插值空间中引入描述裂纹间断的Heaviside函数和描述裂尖奇异性的精化(增强)函数，理性地实现了裂纹的精确描述，日益成为裂纹问题数值方法的研究热点[3-5]。

以无单元伽辽金法EFG(Element-free Galerkin)[6]为代表的无网格法[7]也是裂纹问题数值分析的主要方法之一。与有限元法相比，无网格法的插值(近似)函数不依赖于网格单元，因而具有易于形成高阶近似以及易于实现局部节点加密等优势，给裂纹的数值分析带来便利。实际上，Belytschko等[6]在提出EFG方法时就已经利用其易于局部加密节点的特性有效改善了应力强度因子的计算精度；随后，EFG方法用于稳态和动态裂纹扩展模拟[8,9]，可在很大程度上克服有限元法在模拟裂纹扩展时需要不断重新划分网格的困难；Krysl等[10]将EFG方法应用于三维动态裂纹扩展模拟；Fleming等[11]针对裂尖应力场的奇异性提出了两种精化(强化)函数，不仅减小了应力场的虚假数值振荡，而且提高了应力强度因子的计算精度和效率；Duflot[12]通过向无网格法的权函数中引入精化函数，有效提高了裂尖应力场的解析精度，并将该方法用于三维裂纹扩展分析；近期，无网格法还通过耦合有限元法应用于韧性断裂分析[13]中。

上述工作大多采用了低阶(线性)无网格近似，未能充分利用无网格法易于形成高阶近似，从而有效改善应力场求解精度的优点；另一方面，无网格形函数为非多项式的有理函数，弱形式的数值积分须采用较多积分点，导致计算效率较低[14]，积分精度也不能令人满意。由段庆林等[15,16]提出的基于混合变分原理发展的一致性无网格伽辽金法CEFG(Consistent EFG)通过修正积分点上形函数的空间导数，大幅度减少了所需积分点，并有效改善了计算精度，因而显著提高了无网格法的计算效率，已在三维弹塑性[17]、自适应分析[18]以及不可压缩固体的变形分析[19,20]等问题中获得成功应用，展现出良好的发展潜力。应强调的是，二阶CEFG方法在每个背景三角形积分子域内仅使用三个积分点，但能精确通过线性和二次分片试验，尤其是能得到精度高、光滑无振荡的应力场。考虑到应力解析精度对于裂纹问题至关重要，高阶CEFG方法对于裂纹分析具有显著优势。

目前，CEFG方法还仅限于连续体问题。本文目的是将CEFG方法拓展到以裂纹为特征的非连续体问题。位移在裂纹处的间断采用虚拟节点法(Phantom node method)[21]描述，无需增加额外的节点自由度。为进一步简化方法，与原始的虚拟节点法保持一致，本文也忽略了裂尖奇异场的加强函数，虽然这会导致裂尖解析精度有所降低，但是会大大简化方法的实现，并便于模拟裂纹扩展。这一策略也体现在近期无网格断裂分析的研究中[22-24]。

2 裂纹的数值模型及空间离散

如图1所示，考虑一含裂纹二维弹性体,所占据的区域为Ω,则静力平衡方程可写为

·σ+b=0inΩ

(1)

式中σ为Cauchy应力，b为体力。边界条件有

(2)

(3)

σ·n=0onΓc+

(4)

σ·n=0onΓc-

(5)

为描述裂纹处位移场的不连续性,向位移插值空间中引入间断的Heaviside函数,因而位移近似为

(6)

式中NI(x)为移动最小二乘(MLS)形函数，uI为节点位移参数，qI为附加自由度，H为单位阶跃函数，即

(7)

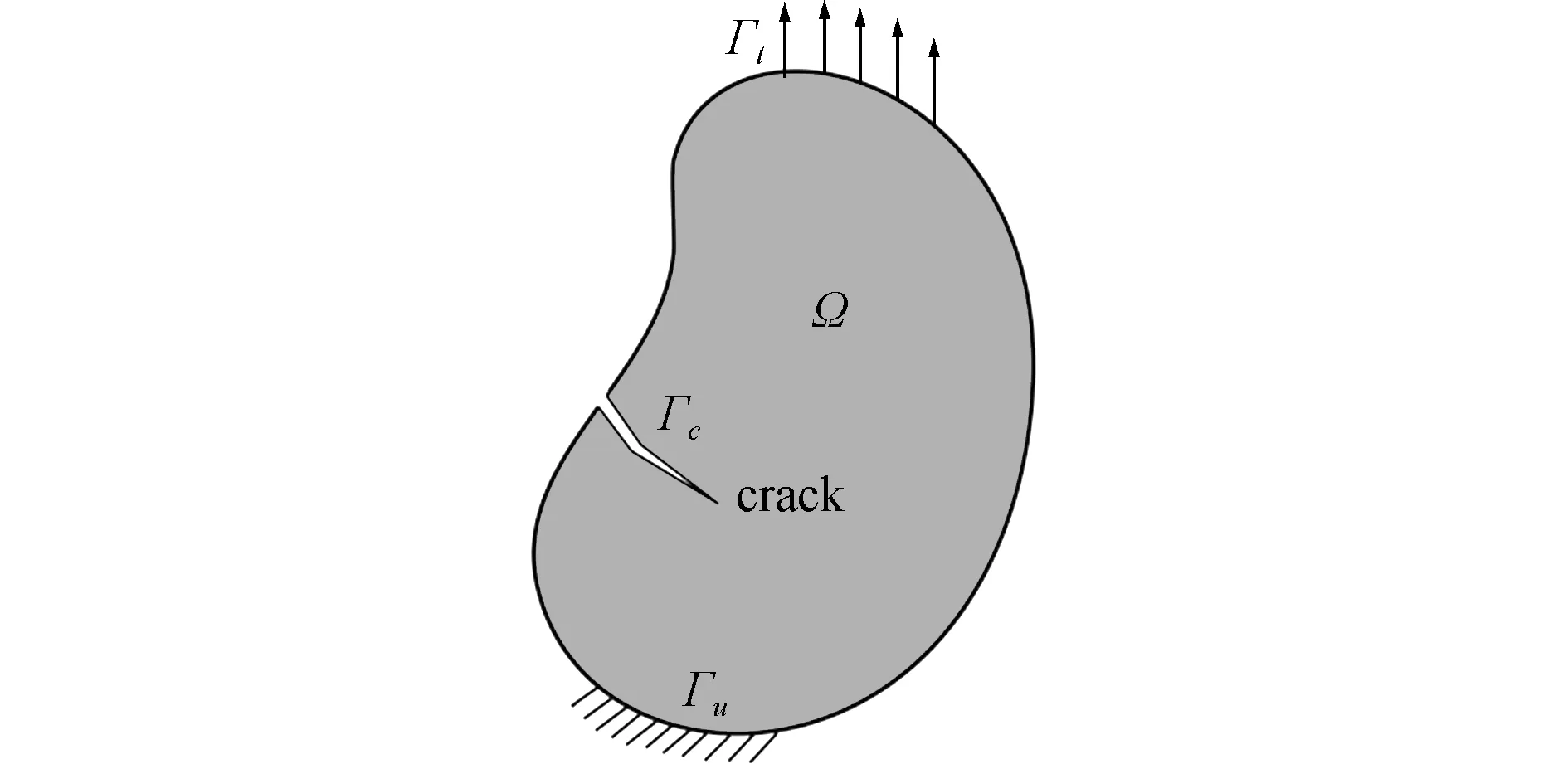
图1 含裂纹二维弹性体示意图

Fig.1 Schematic diagram of a two -dimensional elastic body with a crack

式中f(x)=0表示裂纹面。式(6)右端加uINIH-uINIH,有

(8)

式中H=H(f(x))。为便于推导，将H(-f(xI))记为H-I,H(f(xI))记为H+I。由式(7)可知，当H+I≠0时，H-HI=H-1；当H-I≠0时，H-HI=H,则有

uINIHH+I+uINIHH-I+

qINI(H-1)H+I+qINIHH-I]

(9)

进一步整理可得

uIH+INIH+(uI+qI)H-INIH]

(10)

根据虚拟节点法[21]，式(10)可写为

(11)

式中

(12)

(13)

式(11)表明,含裂纹的位移插值可近似写为两部分的叠加，这一点可结合图2说明。图2的e0为一背景积分单元，实心圆点表示该单元关联的计算节点(即节点形函数在该单元上不等于0的节点)。若该单元发生断裂，则可通过引入虚拟节点(图2的空心圆点)，将该单元拆分成e1和e2两个独立的单元。式(11)的S1与S2分别表示这两个单元的关联节点集合。显然，S1∩S2=∅,即这两个单元没有共享的关联节点，因而可以描述裂纹处的位移间断。同时，这两个单元仍然是连续体，因而其计算同未断裂单元完全一致，只是积分域需取为图中的阴影区域。

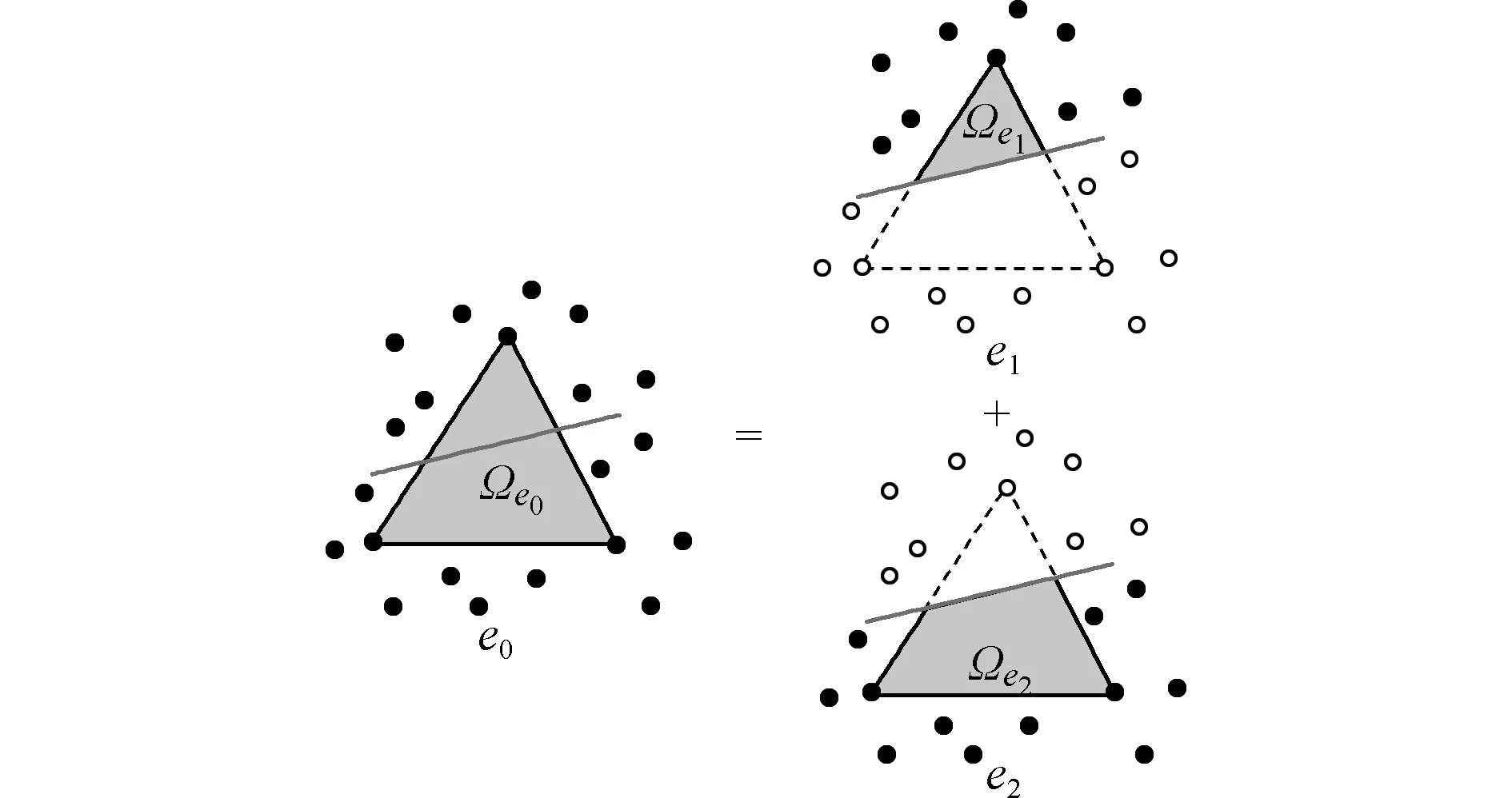
图2 虚拟节点法示意图

Fig.2 Schematic diagram of phantom node method

采用式(11)的位移插值近似，并经过标准的伽辽金过程，可得到控制方程及边界条件式(1～5)的最终离散化方程为

(K-KΓu+βKp)U=f-fΓu+βfp

(14)

式中K为刚度阵，f为等效节点载荷向量，其他矩阵向量由Nitsche法[15](用以施加位移固定边界条件)引入，β为相应的罚系数。对于图2所示的断裂单元，各计算矩阵和向量为

(15)

(16)

(17)

(18)

式中i=1,2分别对应于图2的单元e1和e2，Ωe i为断裂单元的有效域(图中阴影区)，Γi为有效域的边界。

将扩展有限元法中的虚拟节点技术引入到无网格法，无需增加节点额外自由度即可描述裂纹处的位移间断，很大程度上简化了无网格法处理裂纹问题，易于进行程序实现。

3 区域积分：一致性无网格法

如前所述，为提高应力解析精度，本文充分利用无网格法易于形成高阶近似的优点，对位移采用二阶无网格近似。然而，由于二阶MLS形函数为非多项式的有理函数，式(15～17)的区域积分需使用较多积分点，才能保证积分稳定性和精度，严重降低了计算效率[15]。为此，本文采用段庆林等[15,16]提出的一致性无单元伽辽金法(CEFG)，该方法与标准无网格法的不同之处在于区域积分格式和积分点上形函数导数的计算方法。对于本文采用的二阶无网格近似，CEFG方法采用如图3所示的积分格式，即在每个背景三角形单元中使用三个区域积分点(图3的叉点)，在每个三角形边界上使用两个边界高斯点(图3的三角形)。

为得到式(14)的刚度阵K,需计算区域积分点上形函数的导数。区别于标准的无网格方法，该导数在CEFG方法中由如下散度一致性的条件确定[16]。

(19)

式中ΩS为背景积分子域，ΓS为其边界，NI(x)为节点形函数，q(x)=p,x(x)∪p,y(x),p(x)为形成MLS形函数的基底函数向量。对于本文采用的二阶基底p(x)=[1xyx2xyy2]T,有q(x)=p,x(x)∪p,y(x)=[1xy]T,因而式(19)实际上含有3个独立方程。对于每个积分子域，采用图3所示的积分格式计算式(19)的区域和边界积分，可得到相应的3个离散方程，刚好可以求解该子域上3个区域积分点处的形函数导数。为区别于MLS形函数的经典导数[6](通过对形函数直接求导得到)，以上由式(19)确定的形函数导数称为修正导数[15]。文献[15]的工作表明，对于二阶无单元伽辽金法，采用图3所示的积分格式，并使用修正导数计算刚度阵，可大幅提高计算效率并显著改善计算的精度和收敛性，还能得到精确、光滑的应力场，这是本文采用该方法的主要原因。

对于本文研究的裂纹问题，还需进一步考虑背景积分单元发生断裂后,如何构造断裂单元的积分格式。如图4所示，当积分单元发生断裂时，首先，要根据该单元的关联节点生成相应的虚拟节点；然后，将该单元分为两个单元，并根据裂纹位置确定各单元的关联节点(包含虚拟节点);最后，将这两个单元的实际积分域划分成三角形单元，并按图3的积分格式布置积分点。显然，一方面，由于引入了虚拟节点，裂纹处的位移间断可以得到正确描述；另一方面，将实际积分域划分成三角形单元，并按图3的积分格式布置积分点，保证了计算的高效性和准确性。

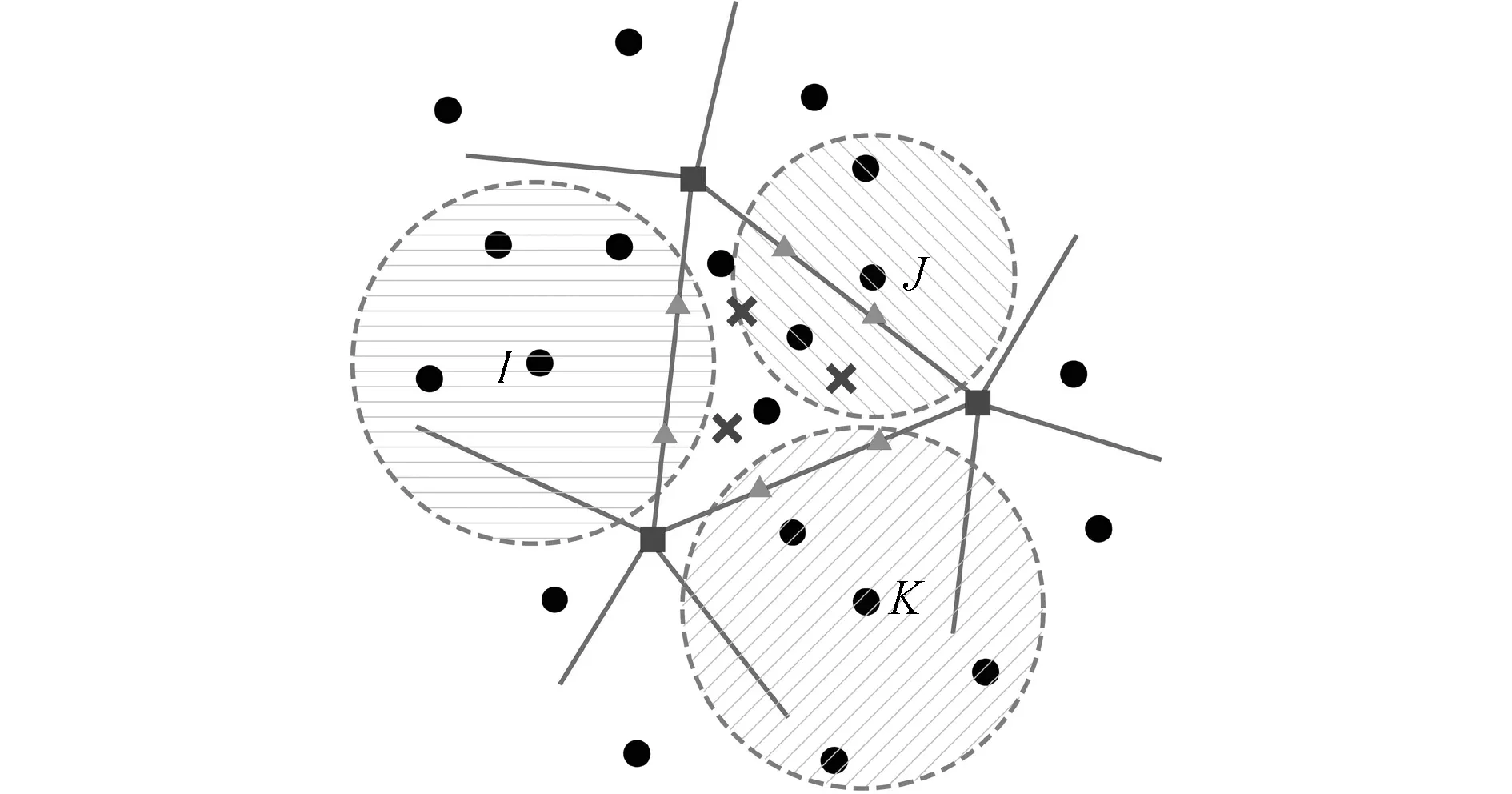
图3 二阶一致性无网格法积分格式示意图

Fig.3 Schematic diagram of the integration scheme for quadraticconsistent element-free Galerkin method

4 裂纹扩展模拟：断裂准则

为模拟裂纹扩展，需确定裂纹的扩展方向。本文采用最大周向应力准则，即裂纹沿着最大周向应力的方向扩展，因而裂纹扩展角度θc由式(20)确定[3]，

KIsinθc+KII(3cosθc-1)=0

(20)

式中KI与KII为裂纹的应力强度因子。式(20)的解可写为

(21)

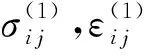
(22)

I(1,2)=2(K(1)IK(2)I+K(1)IIK(2)II)/Eeff

(23)

式中Eeff定义为

图4 断裂单元积分格式示意图

Fig.4 Schematic diagram of the integration schemefor cracked element

(24)

E为弹性模量。因此，若将辅助场选为Mode I断裂模式的裂尖场，即当K(2)I=1,K(2)II=0时，有

(25)

同理，若将辅助场选为Mode II断裂模式的裂尖场，即当K(2)I=0,K(2)II=1时，有

(26)

5 数值算例

采用4个算例考察本文针对断裂问题发展的二阶一致性无单元伽辽金法Q-CEFG处理裂纹问题的有效性。如无特殊说明,所有算例的物理量均采用国际单位制。

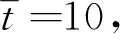
图6显示了本文方法得到的σx x应力场。可以看出，本文处理裂纹问题的Q-CEFG方法能够正确反映该问题上下互不影响的常应力状态[25]，因而精确通过了该分片试验,充分说明了本文方法处理裂纹间断的有效性。

图5 间断分片试验的几何构型和加载示意图

Fig.5 Schematic diagram of the configuration and loading of the discontinuous patch test

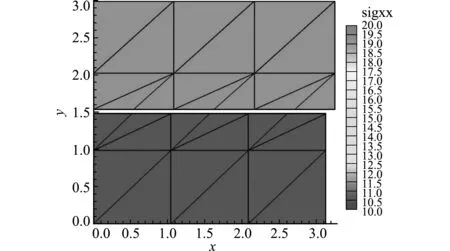
图6 本文方法得到的间断分片试验的σx x应力场

Fig.6σx xfield of the discontinuous patch test obtained by the method of this paper

算例的几何构型如图7所示，顶部受到均匀剪力作用，底部固定，按平面应变问题求解，并取弹性模量E=107,泊松比υ=0.3。考虑到该问题的应力强度因子有准确解KI=34.0,KII=4.55,可以用于比较计算精度，因而除本文建议的Q-CEFG方法外，二阶标准的EFG方法(Q-EFG)和线性一致性无网格法(L-CEFG)也用于该算例的求解。

表1和表2分别显示了三种方法KI和KII的计算结果。可以看出，与采用低阶近似的L-CEFG方法相比，本文Q-CEFG方法得到的应力强度因子更为准确，计算精度高1～2个数量级，说明位移场的高阶近似能有效改善应力场的解析精度，从而能显著提高应力强度因子的计算精度。应强调的是，本文方法没有引入裂尖强化函数，但应力强度因子的计算已相当准确。

与同样采用二阶近似的Q-EFG方法相比，一方面，本文Q-CEFG方法的计算精度更高，尤其是KI的精度约高1个数量级；另一方面，Q-EFG方法由于使用了更多的积分点，因而计算速度明显低于本文的Q-CEFG方法。如采用2232个计算节点时，Q-EFG方法求解位移场消耗的CPU时间大约是本文Q-CEFG方法的2倍。这说明本文的Q-CEFG方法不仅改善了计算精度，而且加快了计算速度，因而显著提高了计算效率。

图7 单边裂纹受到剪切作用

Fig.7 Edge -cracked plate under shear

表1 应力强度因子KI的数值结果

Tab.1 Numerical results of stress intensity factorKI

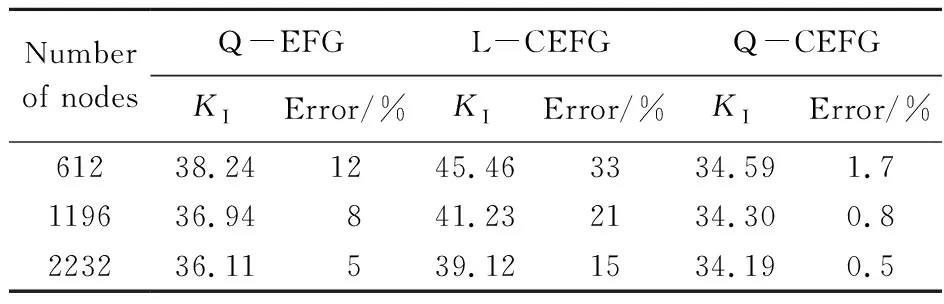
Number of nodesQ-EFG L-CEFGQ-CEFGKIError/%KIError/%KIError/%61238.241245.463334.591.7119636.94841.232134.300.8223236.11539.121534.190.5

表2 应力强度因子KII的数值结果

Tab.2 Numerical results of stress intensity factorK II

Number of nodesQ-EFG L-CEFGQ-CEFGKIIError/%KIIError/%KIIError/%6124.8056.70474.85611964.6215.81274.66222324.51-0.85.46204.540.2

算例用于考察本文Q-CEFG方法预测裂纹扩展路径的能力。如图8所示，一结构部件(图中长度单位为mm)固定于一工字梁上，结构部件一侧的倒角处有一初始裂纹，载荷竖直向上，具体的实验设置可参考文献[27]。取图8的阴影区为计算域，并假定为平面应力问题，材料参数取弹性模量E=2×1011,泊松比υ=0.3,载荷P=1.0,初始裂纹长度a0=5 mm。根据文献[28]，计算域的底部采用固定和铰支约束分别相应于厚梁和薄梁的情况。

计算采用2294个节点，本文方法得到的对应于两种约束情况的裂纹扩展路径如图9所示。可以看出，所得到的路径与Ventura等[28]的结果十分吻合，验证了本文方法模拟裂纹扩展问题的有效性。

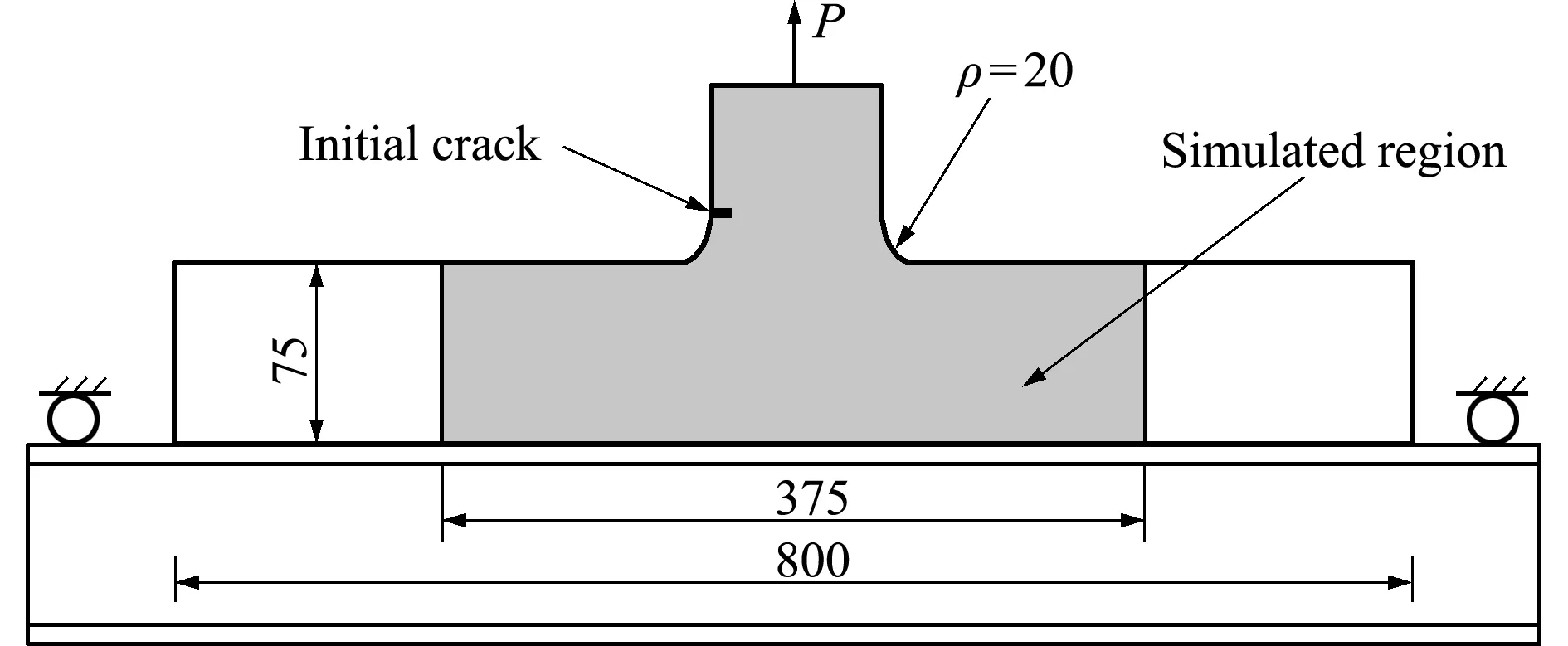
图8 倒角裂纹问题的实验构型和求解域示意图

Fig.8 Experimental configuration and simulated region ofthe crack growth from a fillet problem

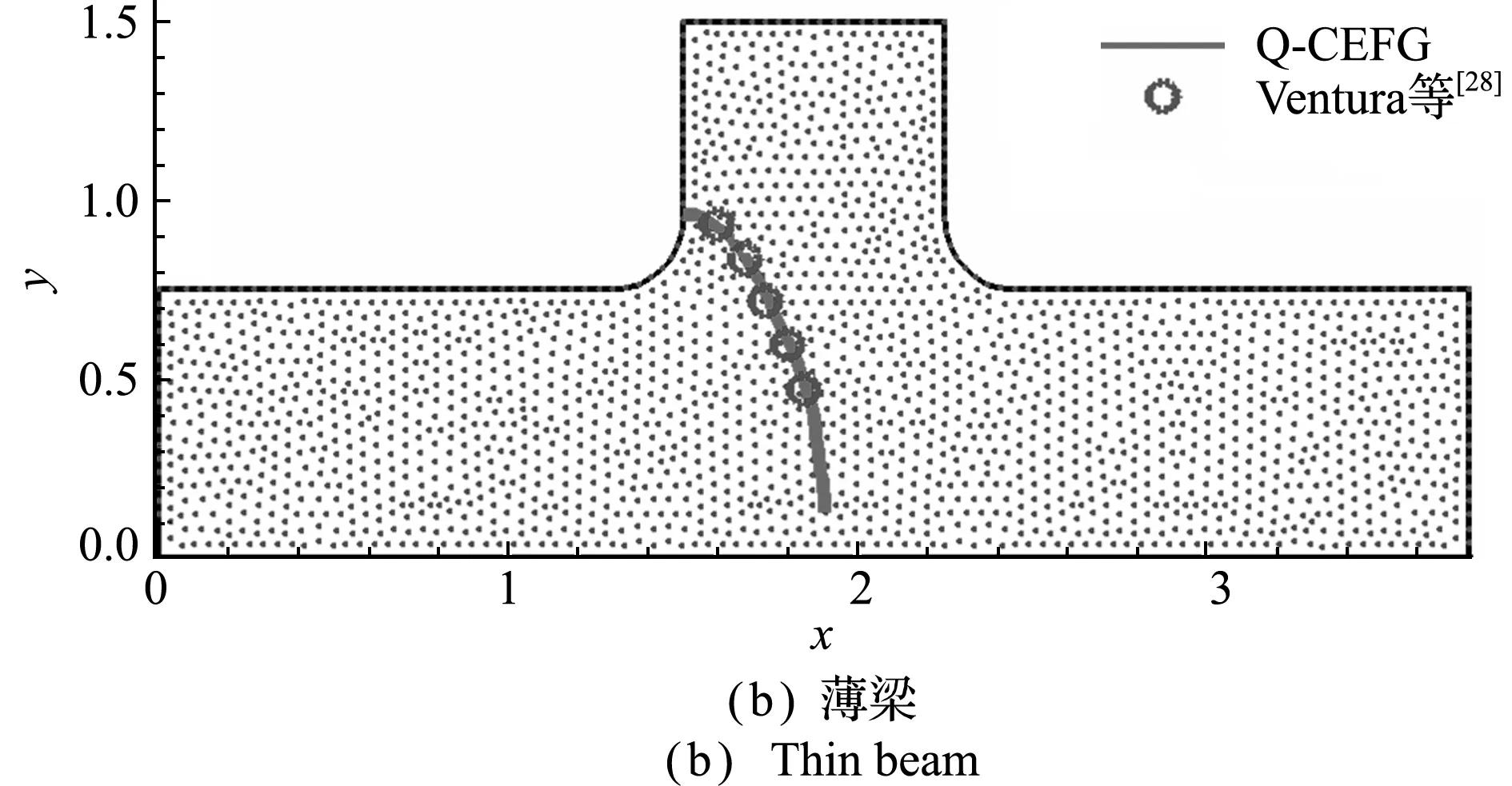
图9 倒角裂纹问题的裂纹路径

Fig.9 Crack trajectory of the crack growth froma fillet problem

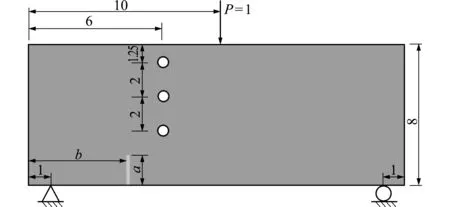
图10 带圆孔的三点弯曲梁示意图

Fig.10 Schematic diagram of the beam with 3 holes subjectedto 3-point bending

为进一步考察本文方法，考虑如图10所示的三孔梁的三点弯曲问题。按平面应力问题求解，并取弹性模量E=3×1010,泊松比υ=0.3。对于梁底部初始裂纹的长度和位置，本文考虑两种情况，情况I为a=1.0,b=4.0；情况II为a=1.5,b=5.0。

采用2602个节点进行计算，得到的两种情况下的裂纹路径如图11所示。图12为本文方法得到的裂纹附近局部放大图及Bittencourt等[29]给出的裂纹路径结果。可以看出，裂纹路径与文献[29]的实验结果吻合良好，再次表明了本文方法模拟裂纹扩展问题的正确性。

图11 三孔梁问题的裂纹路径

Fig.11 Crack trajectory of the beam with 3 holes problem

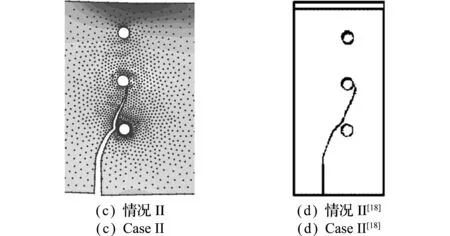
图12 裂纹路径与实验[28]对比

Fig.12 Comparison of crack trajectories with the experimental results[28]

6 结 论

本文将针对连续体的一致性无网格法拓展到以裂纹为特征的非连续体,实现了裂纹扩展过程的数值模拟和裂纹路径的准确预测。一致性无网格法的积分格式和导数修正技术在很大程度上改善了计算精度和效率。其中一个重要发现是高阶无网格法在不引入裂尖强化函数的前提下也能实现应力强度因子的准确计算，而低阶无网格法则导致了相当大的误差。应强调的是，引入裂尖强化函数对于裂纹扩展模拟极其不便，因为计算节点的强化函数需随着裂尖的移动不断地删除和增加。因此，本文的一致性高阶无网格法既能保证应力强度因子的计算精度，又能十分方便地实现裂纹扩展过程的数值模拟，具有很好的发展潜力。

:

[1] Belytschko T，Black T.Elastic crack growth in finite elements with minimal remeshing[J].InternationalJournalforNumericalMethodsinEngineering，1999,45(5):601-620.

[2] Mo⊇s N，Dolbow J，Belytschko T.A finite element method for crack growth without remeshing[J].InternationalJournalforNumericalMethodsinEngineering，1999,46(1)：131-150.

[3] 庄 茁，柳占立，成斌斌,等.扩展有限单元法[M].北京：清华大学出版社，2012.(ZHUANG Zhuo，LIU Zhan-li，CHENG Bin-bin,et al.TheExtendedFiniteElementMethod[M].Beijing:Tsinghua University Press，2012.(in Chinese))

[4] Tian R，Wen L F.Improved XFEM—An extra-DOF free，well-conditioning，and interpolating XFEM[J].ComputerMethodsinAppliedMechanicsandEn-gineering，2015，285:639-658.

[5] 王 振，余天堂.模拟三维裂纹问题的自适应多尺度扩展有限元法[J].工程力学，2016，33(1)：32-38.(WANG Zhen,YU Tian-tang.Adaptive multiscale extended finite element method for modeling three -dimensional crack problems[J].EngineeringMecha-nics,2016,33(1):32-38.(in Chinese))

[6] Belytschko T，Lu Y Y，Gu L.Element-free Galerkin methods[J].InternationalJournalforNumericalMethodsinEngineering，1994,37(2):229-256.

[7] 张 雄，刘 岩.无网格法[M].北京：清华大学出版社，2004.(ZHANG Xiong，LIU Yan.MeshlessMe-thod[M].Beijing：Tisinghua Universtiy Press，2004.(in Chinese))

[8] Lu Y Y，Belytschko T，Tabbara M.Element-free Galerkin method for wave propagation and dynamic fracture[J].ComputerMethodsinAppliedMecha-nicsandEngineering，1995,126(1):131-153.

[9] Belytschko T，Lu Y Y，Gu L，et al.Element-free Galerkin methods for static and dynamic fracture[J].InternationalJournalofSolidsandStructures，1995，32(17/18):2547-2570.

[10] Krysl P，Belytschko T.The Element Free Galerkin method for dynamic propagation of arbitrary 3-D cracks[J].InternationalJournalforNumericalMethodsinEngineering,1999,44(6):767-800.

[11] Fleming M，Chu Y A，Moran B，et al.Enriched element-free Galerkin methods for crack tip fields[J].InternationalJournalforNumericalMethodsinEn-gineering，1997，40(8):1483-1504.

[12] Duflot M.A meshless method with enriched weight functions for three -dimensional crack propagation[J].InternationalJournalforNumericalMethodsinEngineering，2006,65(12):1970-2006.

[13] Shedbale A S，Singh I V，Mishra B K，et al.Ductile failure modeling and simulations using coupled FE-EFG approach[J].InternationalJournalofFracture,2017，203(1-2):183-209.

[14] 张 雄，宋康祖，陆明万.无网格法研究进展及其应用[J].计算力学学报，2003,20(6)：730-742.(ZHANG Xiong，SONG Kang-zu，LU Ming-wan.Research progress and application of meshless method[J].ChineseJournalofComputationalMechanics，2003,20(6):730-742.(in Chinese)).

[15] Duan Q L，Li X K，Zhang H W，et al.Second-order accurate derivatives and integration schemes for meshfree methods[J].InternationalJournalforNumericalMethodsinEngineering，2012，92(4):399-424.

[16] Duan Q L,Gao X，Wang B B，et al.Consistent element-free Galerkin method[J].InternationalJournalforNumericalMethodsinEngineering，2014，99(2):79-101.

[17] Duan Q L，Gao X，Wang B B，et al.A four-point integration scheme with quadratic exactness for three -dimensional element-free Galerkin method based on variationally consistent formulation[J].ComputerMethodsinAppliedMechanicsandEngineering，2014，280(10):84-116.

[18] 邵玉龙，段庆林，高 欣,等.自适应一致性无单元伽辽金法1)[J].力学学报，2017，49(1)：105-116.(SHAO Yu-long，DUAN Qing-lin，GAO Xin,et al.Adaptive consistent high order element-free Galerkin method1)[J].ChineseJournalofTheoreticalandAppliedMechanics，2017，49(1)：105-116.(in Chinese))

[19] Ortiz-Bernardin A，Hale J S,Cyron C J.Volume -ave -raged nodal projection method for nearly-incompressible elasticity using meshfree and bubble basis functions[J].ComputerMethodsinAppliedMechanicsandEngineering，2015，285:427-451.

[20] Ortiz-Bernardin A，Puso M A，Sukumar N.Improved robustness for nearly-incompressible large deformation meshfree simulations on Delaunay tessellations[J].ComputerMethodsinAppliedMechanicsandEngineering，2015，293:348-374.

[21] Song J H，Areias P M A,Belytschko T.A method for dynamic crack and shear band propagation with phantom nodes[J].InternationalJournalforNumericalMethodsinEngineering，2006,67(6):868-893.

[22] Ai W，Augarde C E.An adaptive cracking particle method for 2D crack propagation[J].InternationalJournalforNumericalMethodsinEngineering，2016,108(13):1626-1648.

[23] Kumar S，Singh I V，Mishra B K，et al.Modeling and simulation of kinked cracks by virtual node XFEM[J].ComputerMethodsinAppliedMechanicsandEngineering,2015,283:1425-1466.

[24] Lua J，Zhang T T，Fang E，et al.Explicit phantom paired shell element approach for crack branching and impact damage prediction of aluminum structures[J].InternationalJournalofImpactEngineering，2016,87:28-43.

[25] Dolbow J E，Devan A.Enrichment of enhanced assumed strain approximations for representing strong discontinuities:addressing volumetric incompressibi-lity and the discontinuous patch test[J].InternationalJournalforNumericalMethodsinEngineering，2004,59(1):47-67.

[26] 刘 丰，郑 宏，李春光.基于NMM的EFG方法及其裂纹扩展模拟1)[J].力学学报，2014，46(4):582-590.(LIU Feng，ZHENG Hong,LI Chun-guang.The NMM-based EFG method and simulation of crack propagation1)[J].ChineseJournalofTheoreticalandAppliedMechanics,2014，46(4):582-590.(in Chinese))

[27] Sumi Y，Yang C，Wang Z N.Morphological aspects of fatigue crack propagation Part II—effects of stress biaxiality and welding residual stress[J].Internatio-nalJournalofFracture,1996，82(3):221-235.

[28] Ventura G，Xu J X，Belytschko T.A vector level set method and new discontinuity approximations for crack growth by EFG[J].InternationalJournalforNumericalMethodsinEngineering，2002,54(6):923-944.

[29] Bittencourt T N，Wawrzynek P A，Ingraffea A R，et al.Quasi-automatic simulation of crack propagation for 2D LEFM problems[J].EngineeringFractureMechanics,1996,55(2):321-334.