构造导函数求解抽象函数不等式的策略

广东省深圳市宝安中学(518101)耿玉明

导函数的性质及其运用是高中数学教学的重要内容,其中利用与f′(x)有关的不等式给出的条件,求解与抽象函数f(x)相关联的不等式问题,是考查学生的导函数知识掌握程度的热点内容之一.从数学素养角度看,这类数学问题既可培养学生的逆向思维、整体思想和建构意识,又能考察学生对导函数性质的综合运用能力.其思维导图体现在：观察分析-逆向思维-构造导函数-研究性质-问题求解等几个环节.为了便于学生更好的掌握此类数学问题,笔者从构造导函数的六种类型分别给予分析概述.

类型一 构造f(x)±g(x)+c型导函数

例1设函数f(x)在R上存在导数f′(x),对于任意的实数x,都有f(x)+f(-x)=2x2,且当x∈(-∞,0]时,f′(x)+1＜2x恒成立,若f(m+2)-f(-m)≤2m+2,求实数m的取值范围.

解析依据公式[f(x)±g(x)]′=f′(x)±g′(x),逆向思考：(x2)′=2x,x′=1,根据f′(x)+1＜2x可猜想构造函数g(x)=f(x)-x2+x+c(此处可取c=0),再结合条件研究g(-x)与g(x)及g(m+2)与g(-m)间的关系.

解设g(x)=f(x)-x2+x,则g′(x)=f′(x)-2x+1.当x∈(-∞,0]时,f′(x)+1＜2x,所以g′(x)＜0,即g(x)在(-∞,0]上单调递减.又f(x)+f(-x)=2x2,所以g(-x)+g(x)=f(-x)-x2-x+f(x)-x2+x=f(x)+f(-x)-2x2=0,所以g(x)在R上为奇函数,且在R上为单调递减.又f(m+2)-f(-m)≤2m+2,所以g(m+2)-g(-m)=f(m+2)-f(-m)-2m-2≤0,即g(m+2)＜g(-m).又g(m+2)＜g(-m)⇔m+2≥-m⇔m≥-1,所以m的取值范围是[-1,+∞).

巩固训练1设函数f(x)在R上存在导数f′(x),且不等式恒成立,又f(1)=1,则不等式的解集为()

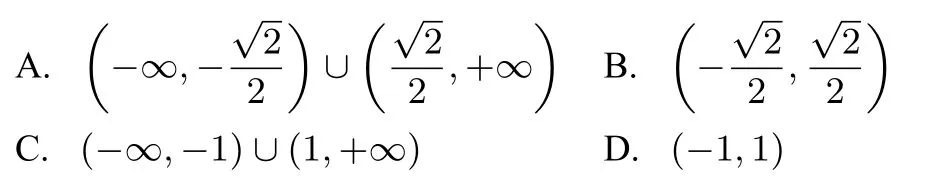
类型二 构造f(x)·g(x)+c型导函数

例2设定义在(-∞,-1)∪(1,+∞)上的函数f(x),对任意的实数x,都有f(1+x)=-f(1-x),当x＞1时,f′(x)+2f(x)＞0恒成立(f′(x)为f(x)的导函数),又f(2)=0,求不等式f(x)·ln|x-1|＜0的解集.

解析依据公式[f(x)g(x)]′=f′(x)g(x)+f(x)g′(x),逆向思考(e2x)′=2e2x,根据条件f′(x)+2f(x)＞0可猜想构造函数g(x)=e2xf(x)+c,再由f(2)=0假定取值g(2)=0,进而求出c=0.

解设g(x)=e2xf(x),则g′(x)=e2x[f′(x)+2f(x)].当x＞1时,f′(x)+2f(x)＞0,所以g′(x)＞0,即g(x)在(1,+∞)上为增函数,又g(2)=e4f(2)=0,所以x∈(1,2)时g(x)＜0;x∈(2,+∞)时g(x)＞0.即x∈(1,2)时f(x)＜0;x∈(2,+∞)时f(x)＞0.又f(1+x)=-f(1-x),所以f(x)关于点(1,0)对称.所以x∈(-∞,0)时f(x)＜0;x∈(0,1)时f(x)＞0.所以

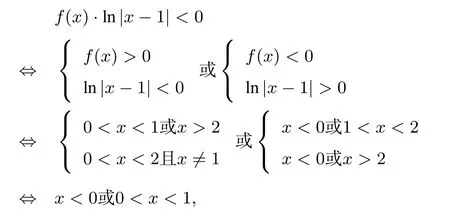
所以不等式的解集为(-∞,0)∪(0,1).

巩固训练2已知f(x)是定义在R上的减函数,其导函数为f′(x),且满足恒成立,则下列结论正确的是()

A.对任意的x∈R,f(x)＞0

B.对任意的x∈R,f(x)＜0

C.当且仅当x∈(-∞,1)时,f(x)＜0

D.当且仅当x∈(1,+∞)时,f(x)＞0

类型三 构造型导函数

例3定义在R上函数f(x)的导函数为f′(x),对任意实数x都有f′(x)＜2f(x)恒成立,且f(x+1)为偶函数,又求不等式的解集.

解析依据公式逆向思考(e2x-m)′=2e2x-m,根据条件f′(x)＜2f(x)可猜想构造函数再由f假定取值进而求出m=1,c=-1.

解设则

因为f′(x)＜2f(x),所以g′(x)＜0,所以g(x)在R上为单调递减函数.因为f(x+1)为偶函数,所以f(x+1)=所以

即x≥1,所以不等式的解集为[1,+∞).

巩固训练3已知定义在(0,+∞)上函数f(x)的导函数为f′(x),且不等式f′(x)(xlnx2)＞2f(x)恒成立,则有()

A.6f(e)＞2f(e3)＞3f(e2)B.6f(e)＜3f(e2)＜2f(e3)

C.6f(e)＞3f(e2)＞2f(e3)D.6f(e)＜2f(e3)＜3f(e2)

类型四 构造f(x)g(x)+h(x)+c型导函数

例4定义在R上函数f(x)的导函数为f′(x),若函数f(x+1)关于x=-1对称,且又当x∈(-∞,0)时,2f(x)+xf′(x)＞1恒成立,求不等式的解集.

解析依据公式[f(x)g(x)]′=f′(x)g(x)+f(x)g′(x),逆向思考(x2)′=2x,根据条件2f(x)+xf′(x)＞1可猜想构造函数取g(1)=0,进而求出c=1.

解因为函数f(x+1)关于x=-1对称,所以f(-x)=f(x),即f(x)为偶函数.设则g′(x)=2xf(x)+x2f′(x)-x=x[2f(x)+xf′(x)-1].又x∈(-∞,0)时,2f(x)+xf′(x)＞1恒成立,所以x∈(-∞,0)时,g′(x)＜0,即g(x)在(-∞,0)上单调递减.又g(-x)=为偶函数,且g(1)=

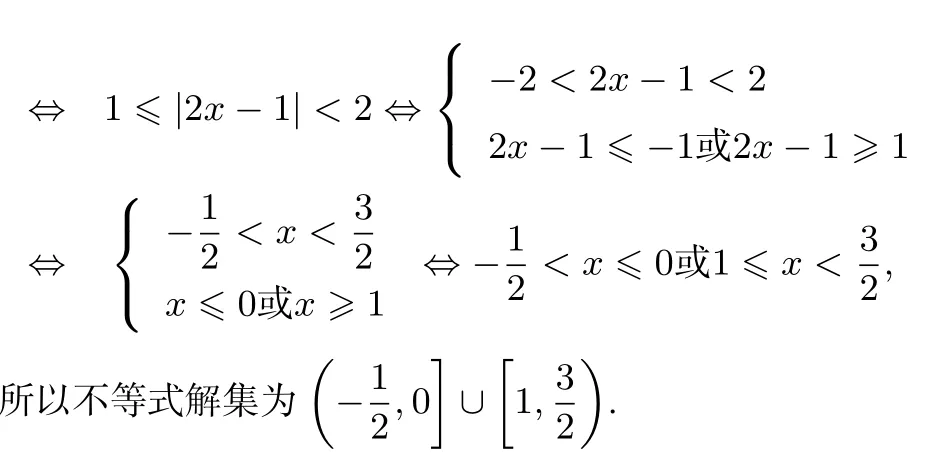
巩固训练4定义在R上函数f(x)的导函数为f′(x),若对任意的x,都有2f(x)+xf′(x)＜2恒成立,且f(-x)=f(x),则使4x2f(-2x)-f(1)＜4x2-1成立的x的范围为()

类型五 构造型导函数

例5定义在上的函数f(x)同时满足f(x+π)=-f(x),且时,恒有f′(x)+tanxf(x)-2cos2x＜0成立(f′(x)为f(x)的导函数),求不等式f(x)-sin2x+cosx≥0的解集.

解析依据公式逆向思考(cosx)′=-sinx,(sinx)′=cosx,根据条件f′(x)+tanxf(x)-2cos2x＜0可猜想构造函数g(x)=-2sinx+c,再由进而求出c=1.

解设g(x)=

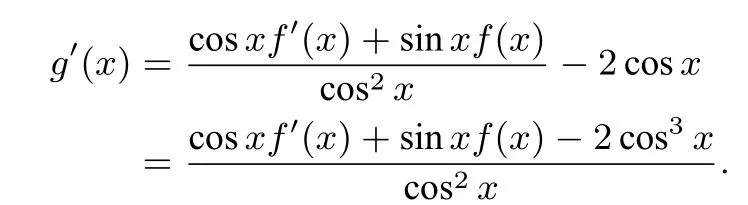
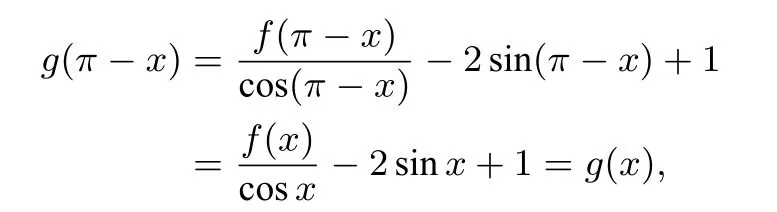
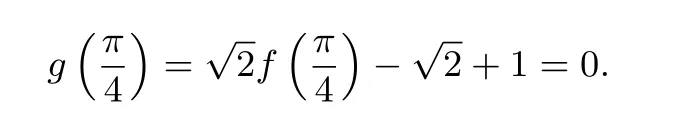
又由f(x+π)=-f(x)得,f(x+2π)=f(x),所以

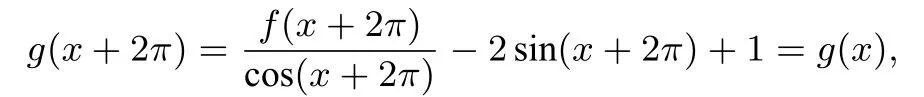
所以函数g(x)的周期为2π.由f(x)-sin2x+cosx≥0得,

即

所以解集为

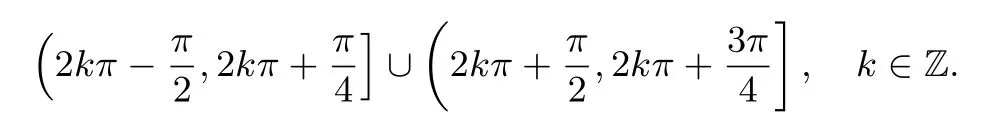
巩固训练5定义在R上函数f(x)的导函数为f′(x),若对任意的x,都有f′(x)-f(x)＜ex恒成立,则下列不等式成立的是()

A.f(1)-ef(0)＞eB.f(0)-ef(-1)＞1

C.f(2)-ef(1)＞e2D.ee-1f(1)-f(e)＞ee(1-e)

类型六 构造[f(x)]n+h(x)+c型导函数

例6定义在(0,+∞)上函数f(x)的导函数为f′(x),对任意的x∈(0,+∞),都有xf(x)f′(x)＜1恒成立,若不等式f2(x2+mx)-f2(1)≤2ln(x2+mx)在[1,4]上有解,求实数m的取值范围.

解析依据公式[fn(x)]′=nfn-1(x)f′(x),逆向思考根据条件xf(x)f′(x)＜1可猜想构造函数g(x)=f2(x)-2lnx+c,这里可取c=0.

解设g(x)=f2(x)-2lnx,则

当x∈(0,+∞)时,xf(x)f′(x)＜1,所以g′(x)＜0.所以g(x)在(0,+∞)上是单调递减函数.由f2(x2+mx)-f2(1)≤2ln(x2+mx)得f2(x2+mx)-2ln(x2+mx)≤f2(1),即g(x2+mx)≤g(1)在[1,4]上有解.即x2+mx≥1在[1,4]上有解,即在[1,4]上有解.设因为h(x)在[1,4]上为减函数,所以所以m的取值范围是

巩固训练6定义在R上的函数f(x)满足f(x)＞0,其导函数为f′(x),且当x∈(-∞,1)时,恒有2(x-1)f2(x)＞f′(x),若a,b∈R,则不等式f(b)-f(a)＞(b-a)(b+a-2)f(a)f(b)成立的一个充分条件是()

A.a＞b＞1B.b＞a＞1

C.b＜1＜aD.a＜1＜b

巩固训练答案：1.C;2.A;3.B;4.B;5.D;6.B.