一抽象函数性质的探究

山东省单县教研室(274300)周启杰

一、问题提出

题目(2010年高考福建省理科第15题)已知定义域为(0,+∞)的函数f(x)满足：

(1)对任意x∈(0,+∞),恒有f(2x)=2f(x)成立;

(2)当x∈(1,2]时,f(x)=2-x.给出如下结论：

①对任意m∈Z,有f(2m)=0;

②函数f(x)的值域为[0,+∞);

③存在n∈Z,使得f(2n+1)=9;

④“函数f(x)在区间(a,b)上单调递减”的充要条件是“存在k∈Z,使得(a,b)⊆(2k,2k+1).”

其中所有正确结论的序号是____.

(正确答案为：①,②,④.解析从略.)

该题考查了一个抽象函数：f(2x)=2f(x),利用x∈(1,2]时f(x)=2-x将函数f(x)定义为具体的分段函数.从图象变换的角度,我们可以直观得到函数图象,避免赋值迭代技巧.设P(x0,y0)是函数f(x)图象上任意一点,那么由f(2x)=2f(x),得f(2x0)=2f(x0)=2y0,即点(2x0,2y0)也在函数f(x)的图象上.也就是说,f(x)图象上任意一点的横坐标、纵坐标都变为原来的2倍后,对应的点仍在函数的图象上.反过来,f(x)图象上任意一点的横坐标、纵坐标都变为原来的倍后,对应的点也在函数的图象上.因此,按照这种伸缩变换,可以画出函数的图象(如图1).

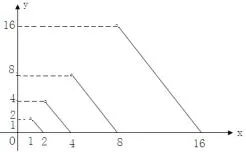
图1

可以看出,性质f(2x)=2f(x)的本质是图象的伸缩变换.为什么在(1,2]上定义函数呢?由(1,2]上的图象,可以向右无限扩展,但向左扩展,似乎有个“界限”,那么这个“界”是谁呢?函数的定义域为什么是(0,+∞)呢?

二、问题解决

如果在区间(a,b](a＜b)上定义函数,那么利用f(2x)=2f(x)一次次作用,对应区间分别为

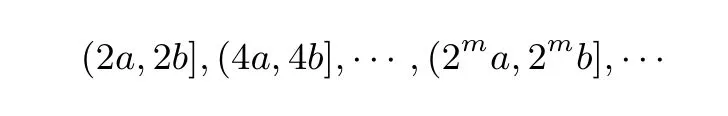
其中m∈N+.当b=2a时,由a＜b知a＞0,上述区间沿x轴正方向依次排列,此时相邻区间彼此刚好相连.

其中m∈N+,这些区间沿x轴负方向依次排列,相邻区间彼此刚好相连.由于可知函数图象向左扩展时的“界限”就是x=0,函数的定义域就是(0,+∞).

也就是说,若函数f(x)满足f(2x)=2f(x),如果在区间(a,2a](a＞0)上定义f(x),那么f(x)在区间(2ma,2m+1a](m∈Z)上也有定义,函数定义域为(0,+∞).

同样,如果在区间[2a,a)(a＜0)上定义f(x),那么f(x)在区间[2m+1a,2ma)(m∈Z)上也有定义,函数定义域为(-∞,0).

除个别情形外,满足f(2x)=2f(x)的函数f(x)一般是分段函数,上述结论给出了将函数f(x)定义为分段函数的方法.这种定义方法保证了函数的定义域是(0,+∞)或(-∞,0),定义域达到了“最大化”,我们说这样的定义是完美的.

至此,可得到更一般地情形：

如果函数f(x)满足f(mx)=nf(x)(m＞1),若在(a,ma](a＞0)上定义函数,则函数在(mka,mk+1a](k∈Z)上也有定义,其定义域为(0,+∞);若在区间[ma,a)(a＜0)上定义函数,则函数在区间[mk+1a,mka)(k∈Z)上也有定义,其定义域为(-∞,0).

若函数满足f(x)满足f(mx)=nf(x)(0＜m＜1),由于就转化为上一种情形了.

三、深度探究

下文我们约定：对于已知解析表达式或者已知某种性质的函数,在没有明确指出其定义域时,总假定其定义域是满足给定条件或者已知条件成立的最大的实数集.

我们知道,满足f(x+t)=f(x)(t/=0)的函数f(x)为周期函数;满足f(t-x)=f(x)的函数f(x)为轴对称函数;满足f(t-x)=-f(x)的函数f(x)为中心对称函数.

如果函数f(x)对任意x满足f(x+t)=kf(x)(kt/=0),我们可以称f(x)为类周期函数,|t|为它的一个“周期”.例如,若函数f(x)满足f(x+1)=2f(x),选择长度为1的一个区间定义之：x∈[0,1)时,f(x)=x,则f(x)的图象如图2所示;若函数f(x)满足f(x+1)=-2f(x),可定义之：x∈[0,1)时,f(x)=x,则f(x)的图象如图3所示.

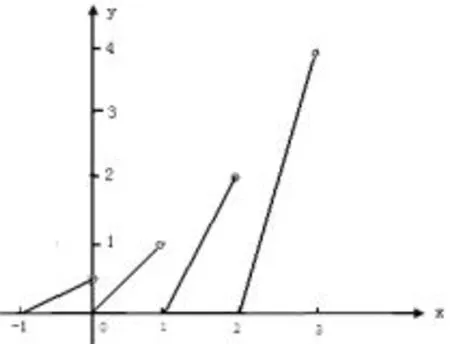
图2

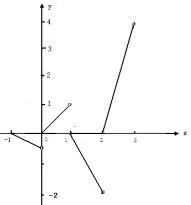
图3

如果函数f(x)对任意x满足f(t-x)=kf(x)(k/=0),我们可以称f(x)为类对称函数,k＞0时,直线为它的“对称轴”;k＜0时,点为它的“对称中心”.

例如,如果函数f(x)满足f(1-x)=2f(x).若定义：

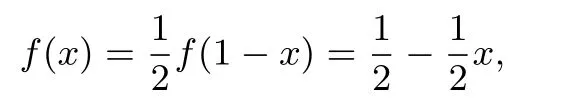
f(x)的图象如图4所示.

如果函数f(x)满足f(1-x)=-2f(x).若定义：

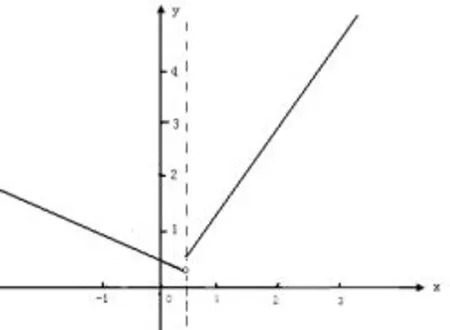
图4

图5

考虑更一般情况：若函数f(x)满足f(ωx+t)=kf(x)(ω/=0,ω/=1,ω/=-1,k/=0),f(x)一般是分段函数,那么如何选择一个恰当的区间,将它定义为完美的分段函数呢?

下面从具体问题入手,来说明如何将f(x)定义为分段函数的方法,并揭示其图象特征.

问题1如果函数f(x)满足f(2x+1)=f(x),如何选择一个区间将函数f(x)定义为分段函数?函数图象有何特征呢?

如果在区间(m,n](m＜n)定义函数,利用f(2x+1)=f(x)作用一次,与(m,n]对应的区间为(2m+1,2n+1];在(2m+1,2n+1]上作用一次,对应区间(2(2m+1)+1,2(2n+1)+1],即

作用k次后,得区间

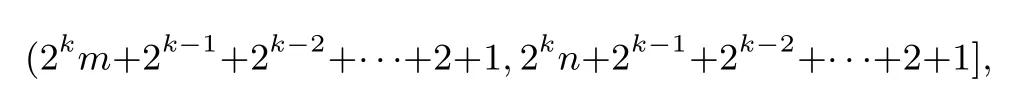
即

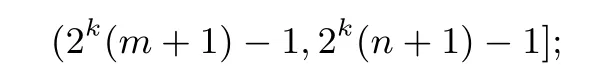
作用k+1次后,得区间(2k+1(m+1)-1,2k+1(n+1)-1].令2m+1=n,由m＜n,得m＞-1.则m＞-1且n=2m+1时,

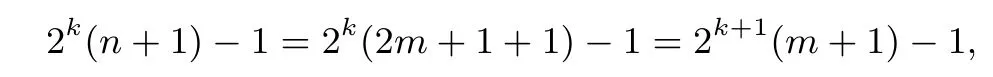
这说明m＞-1且n=2m+1时通过f(2x+1)=f(x)的一次次作用,对应的区间依次沿x轴正方向排列,且相邻的区间刚好连接.同时,

通过f(x)=作用一次,与(m,n]对应的区间为

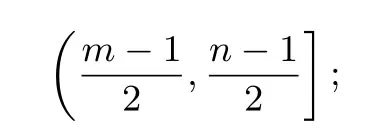
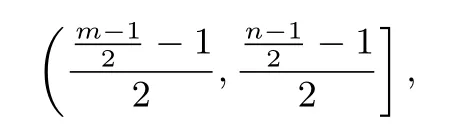
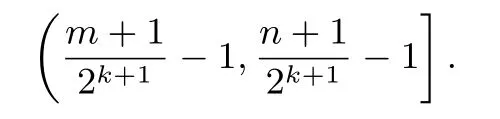
由m＞-1且n=2m+1,易知即m＞-1且n=2m+1时通过f(x)=一次次作用,对应的区间依次沿x轴负方向排列,且相邻的区间刚好连接.由m+1＞0知

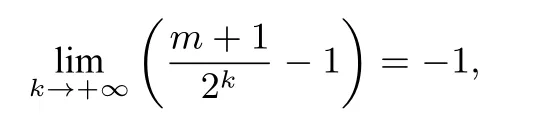
故函数的定义域就是(-1,+∞).

从函数图象变换的角度看,在函数f(x)图象上任取一点P(x0,y0),通过f(2x+1)=f(x)作用,f(2x0+1)=f(x0)=y0,故函数在各段上的函数值的集合相等.函数的“界”,即函数的定义域(-1,+∞)的左端点值-1,可由2x+1=x解得.

例如,如果函数f(x)满足f(2x+1)=f(x),令m=1,则n=2×1+1=3,不妨定义：x∈(1,3]时,f(x)=x,则f(x)的图象如图6所示.

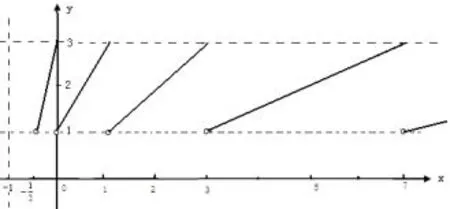
图6

那么,满足f(2x+1)=f(x)的函数定义域能否为(-∞,-1)呢?事实上,在区间[m,n)(m＜n)定义函数,当n＜-1且m=2n+1时,函数定义域就是(-∞,-1)(验证略).

同样,如果函数f(x)满足f(2x-1)=f(x),若在(m,n](m＜n)上定义函数,其中m＞1且n=2m-1,这样就把f(x)定义为分段函数了,其定义域为(1,+∞)(验证略).

问题1及下面的问题2都有一般性的结论,不再赘述.

问题2如果函数满足f(1-2x)=f(x),如何选择一个区间将函数f(x)定义为分段函数?

若在(m,n](m＜n)上定义函数,利用f(1-2x)=f(x)一次次作用,依次得对应区间：[1-2n,1-2m);(1-2(1-2m),1-2(1-2n)],即(22m-2+1,22n-2+1];[1-2(22n-2+1),1-2(22m-2+1)),即[-23n+22-2+1,-23m+22-2+1);(1-2(-23m+22-2+1),1-2(-23n+22-2+1)],即(24m-23+22-2+1,24m-23+22-2+1],···,作用2k-1次得

作用2k+1次得

令22m-2+1=n,即4m-1=n,由m＜n,得且4m-1=n时,

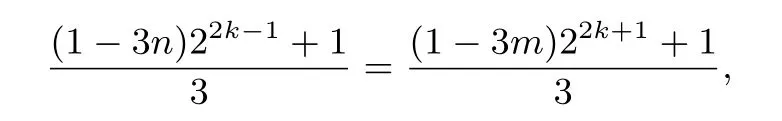
即作用奇数次时,对应的区间沿x轴负方向排列,相邻的两个区间刚好连接.作用2k次得

即作用偶数次时,对应区间依次沿x轴正方向排列,相邻的两个区间刚好连接.故且4m-1=n时,利用f(1-2x)=f(x)一次次作用,函数向左右两边跳跃扩展,相邻的两个区间刚好连接.

同时,

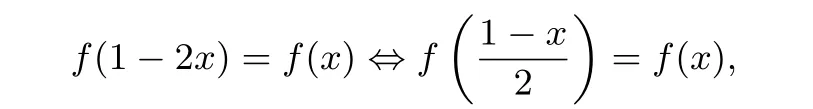
而

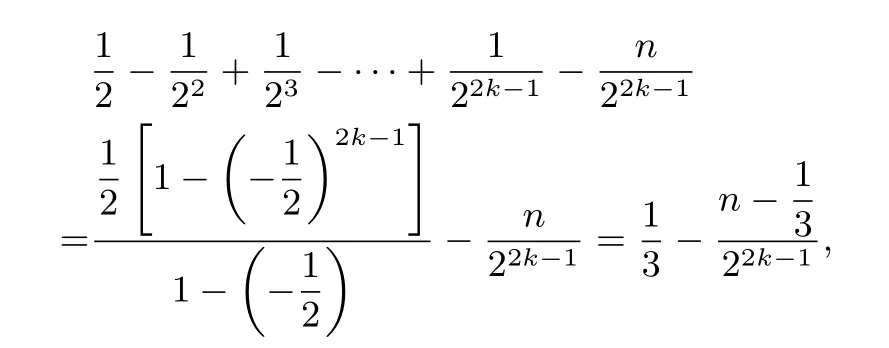
即作用2k-1次后,对应区间为

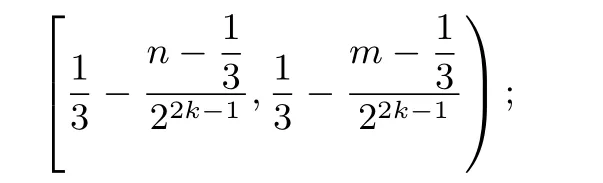
作用2k+1次后,对应区间为

f(x)作用奇数次时,对应区间依次沿x轴正方向排列,相邻区间刚好连接,函数依次从左边向直线靠拢.

作用2k次后,对应区间为

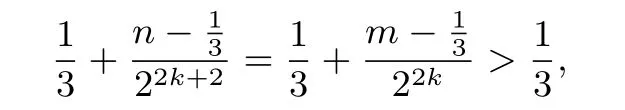
从函数图象变换的角度看,在函数f(x)图象上任取一点P(x0,y0),通过f(1-2x)=f(x)作用,f(1-2x0)=f(x0)=y0,故函数在各段上的函数值的集合相等.

例如,如果函数f(x)满足f(1-2x)=f(x),令m=1,则n=4m-1=3,

若定义x∈(1,3]时,则f(x)的图象如图7所示.

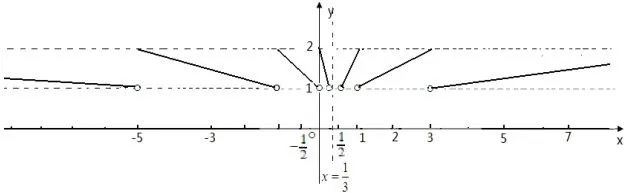
图7

同样,如果函数f(x)满足f(1-2x)=f(x),也可以选择区间[m,n)来定义函数,其中m=4n-1(验证略).

问题3若函数f(x)满足f(2x+1)=3f(x),试选择一个区间,将f(x)定义为分段函数,并作出其图象.

分析该问题与问题1一样,只不过函数在各段上的函数值的集合不等罢了.

由问题1知,令m=1,则n=2m+1=3,可定义：x∈(1,3]时,则f(x)的图象如图8所示.

图8

问题4如果函数f(x)满足f(1-2x)=2f(x),试选择一个区间,将f(x)定义为分段函数,并作出其图象.

分析该问题与问题2一样,只不过函数在各段上的函数值的集合不等罢了.

由问题2知,令m=1,则n=4m-1=3,不妨定义：x∈(1,3]时,则f(x)的图象如图9所示.

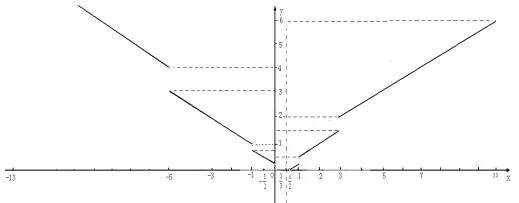
图9