椭圆方程最优控制问题的数值算法研究

高 新，袁健华



椭圆方程最优控制问题的数值算法研究

高 新，袁健华

（北京邮电大学校理学院，北京 100876）

本论文引入原对偶方法（P-D）以及交替方向乘子法（ADMM）两种算法求解椭圆方程约束的最优控制问题，要讨论的椭圆方程是一种对流扩散方程。论文解决了在无状态约束和盒子约束的情况下对流扩散方程控制的问题。本文首先分析了最优控制模型解的存在唯一性以及一阶最优性条件，随后利用有限元方法将原始优化模型转换成优化离散系统。此后，利用P-D以及ADMM分别求解离散优化系统。ADMM是具有对偶上升法的可分解性以及乘子法的全局收敛性两大优势的一阶收敛算法，另外P-D也是具有全局收敛的一阶收敛算法。本论文目的在于将P-D和ADMM两种算法在收敛速率维度上进行比较。最后从数值实验中得出ADMM的收敛速率快于P-D，证实了ADMM是一个高效的优化算法。

最优控制；椭圆方程约束；交替方向乘子法；原对偶方法；有限元

0 引言

偏微分方程（PDE）约束的最优控制问题，起初是在80年代的法国数学家J.L.Lions的著作《Optimal control of systems governed by partial differential equations》中提出的[1]，现已成为非常受关注的交叉学科。偏微分方程约束的最优控制问题有十分广泛的应用，涵盖了物理，化学，甚至工程设计领域，比如水库管理，医疗器械的形状优化，天气预报，热现象，流体问题等。

为解决PDE最优控制问题，很多学者已经提出了多种有效的算法，其中牛顿型迭代解法较为常见[2]。牛顿迭代解法具有局部二阶收敛的性质，但是很多种牛顿迭代求解的方法对迭代初始点的选取非常严格[3]。所以如何选取具有全局收敛且收敛速度快的算法非常重要。

另外，无论用什么方法求解，约束条件中的偏微分方程需要借用适当的离散方法转换成离散系统，在已有的大部分数值算法中控制变量和状态变量是耦合在一起的，这样就会消耗大量的计算资源去完成求解。

为了解决上述两个问题，本文引入了交替方向乘子法(ADMM)。ADMM具有全局收敛性且在迭代求解过程中控制变量和状态变量为交替迭代，从而大大减少了计算复杂度。在浏览文献过程中，发现很少学者将ADMM算法用到解决PDE约束的最优控制问题上。同时本文也引入了原对偶方法(P-D),它也是具有全局收敛性的有效算法,并且受到不少学者的青睐[4]。

本论文讨论的偏微分方程是一种对流扩散方程[5]，对流扩散方程在环境科学，电子科学和流体力学等方面有着广泛的应用。关于对流扩散方程的求解，目前已经取得了一系列的成果[6]。本文首次尝试用上述两种算法通过有限元离散求解由对流扩散方程约束的最优控制问题。对两种算法进行收敛速率的比较，经数值实验证实了ADMM的高效性。

1 模型问题

1.1 模型问题

本文研究以下形式的最优控制问题：

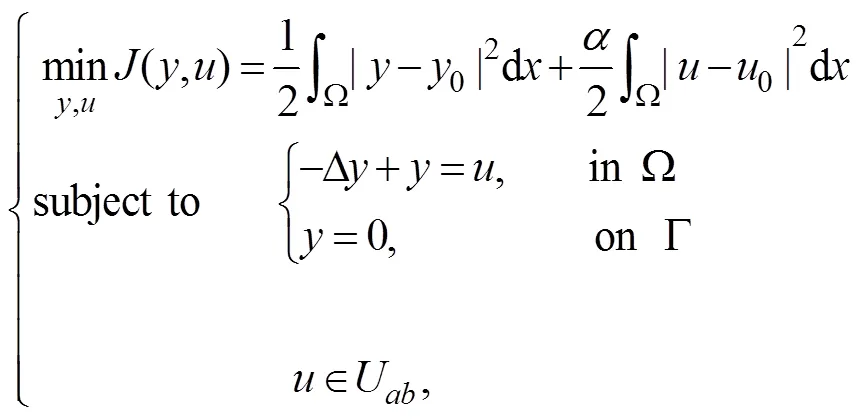
1.2 模型解的存在及唯一性

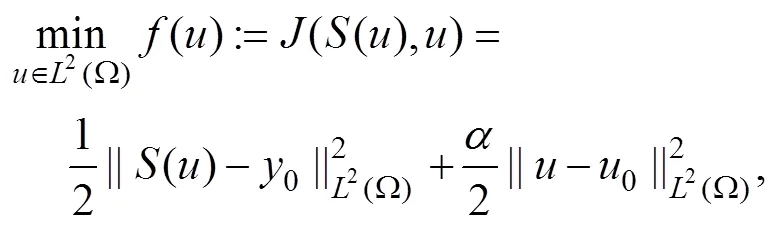
引理1.1的证明在文献[9]中已经提到，这里就不予证明。

定理1.2 问题（1.2）在有、无控制约束条件下均存在全局最优解。

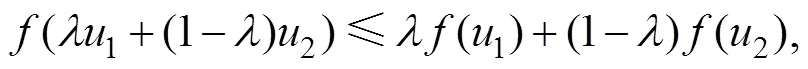
成立。

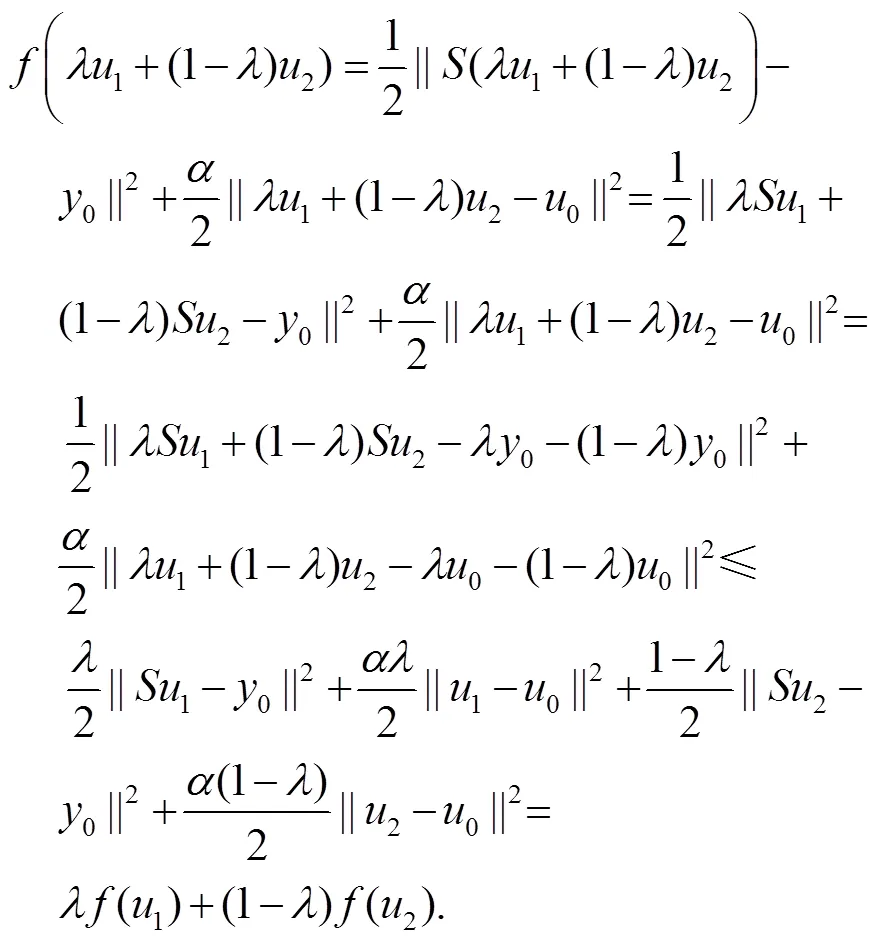
1.3 一阶最优性条件

为了推导出最优性条件，构造问题（1.1）的Lagrange函数：

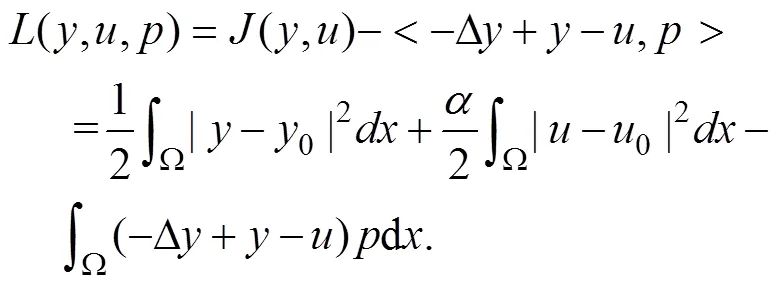
一阶最优性条件满足下列方程组：

故得到问题(1.1)的一阶最优性条件：

原方程：

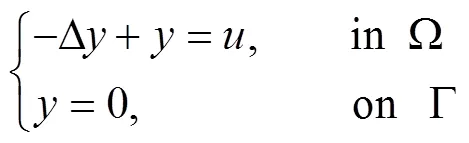
伴随方程（对偶方程）：

变分不等式：

2 变分和有限元离散

为了进行有限元离散，我们先要给出问题（1.1）的变分形式，再利用有限元离散，最终获得离散优化系统。

2.1 变分问题

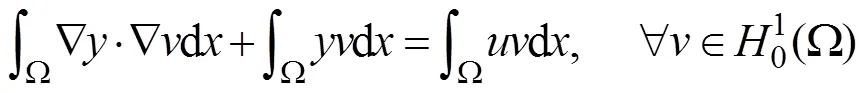
2.2 有限元离散

接下来利用有限元离散，有限元离散的具体步骤如下[10]:

3. 有限元空间。令：

4. 有限元离散形式。

5. 基函数的选取。

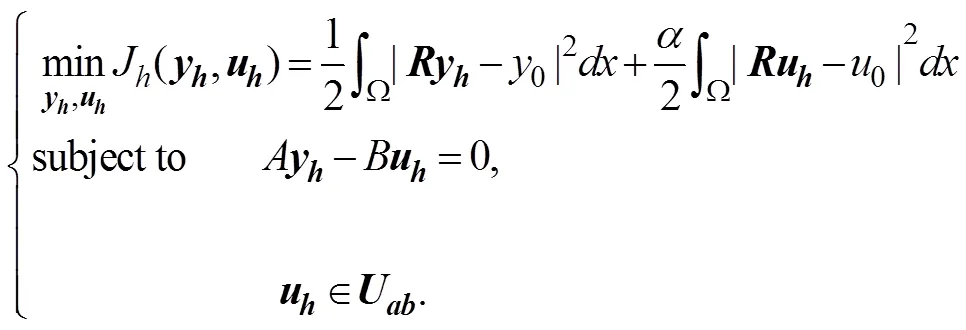
同理一阶最优性条件的离散形式如下：

原约束条件的离散形式：

伴随方程（对偶方程）的离散形式：

变分不等式的离散形式：

3 原对偶方法和交替方向乘子法

3.1 原对偶方法

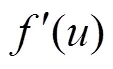
算法一：无状态约束条件的P-D算法

算法二：盒子约束条件的P-D算法

3.2 交替方向乘子法

交替方向乘子法（ADMM）算法是先离散后优化的算法，它是基于很多优化算法不断优化得来的，包括对偶上升法，对偶分解以及增广拉格朗日乘子法，且ADMM具有全局收敛性[12]。

接下来解决下列的鞍点问题：

算法三：无状态约束条件的ADMM算法

（2）交替迭代计算：

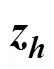
可知看出上述优化系统与问题（2.4）是等价的。故对这个优化系统进行ADMM求解。同样，写出增广拉格朗日函数：

那么问题（1.1）在盒子约束条件下的ADMM算法步骤如下：

算法四：盒子约束条件的ADMM算法

（2）交替迭代计算：

4 数值实验

数值实验分为两种情况，一种是问题（1.1）在无状态约束条件下的情况，另一种是盒子约束的情况，每种情况又包括两部分，分别是：

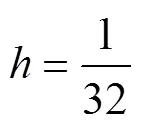
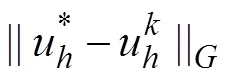
算例一:无状态约束情况

从图3易知算法三的收敛速率快于算法一的收敛速率，即ADMM的收敛速率快于P-D算法的收敛速率。

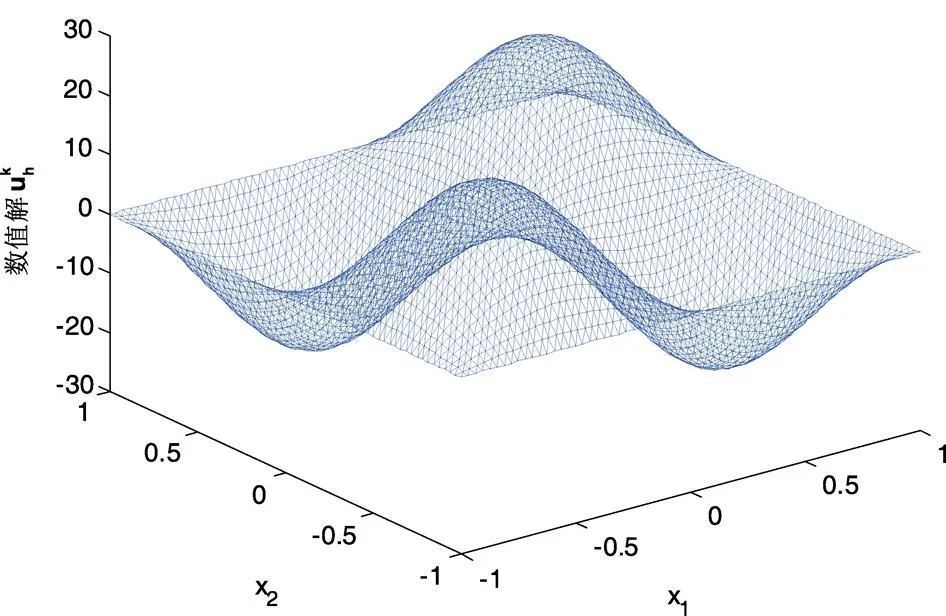
图1 算法一的的数值解图像

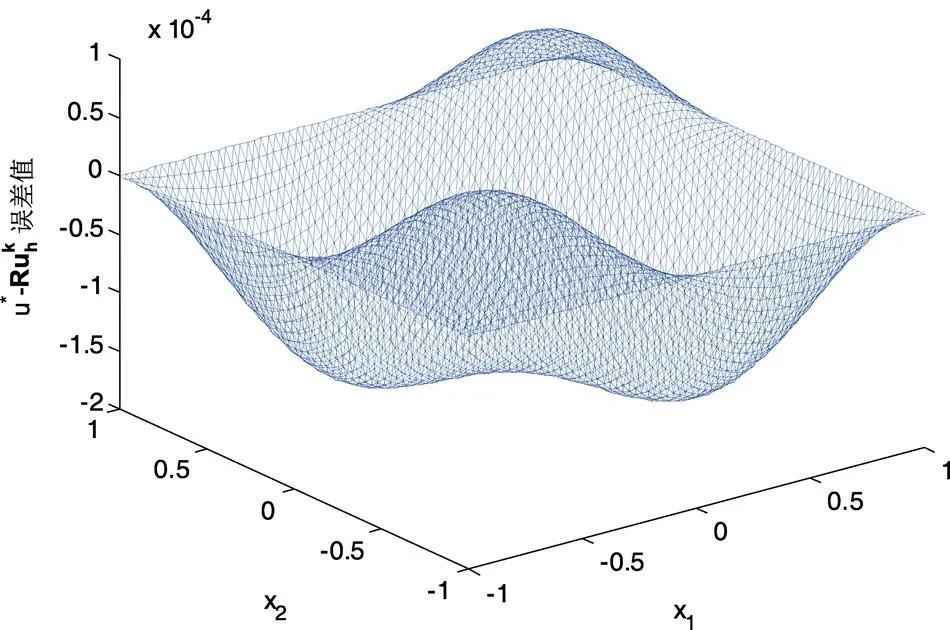
图2 算法一的的误差图像

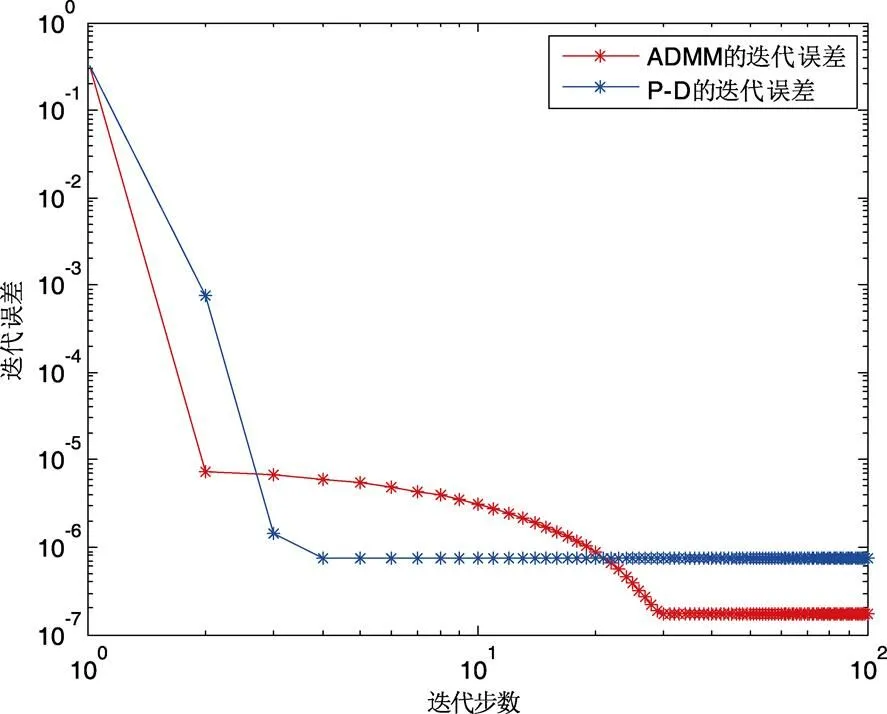
图3 算法一和算法三的收敛速率对数图像

算例二：有状态约束条件（盒子约束）的情况

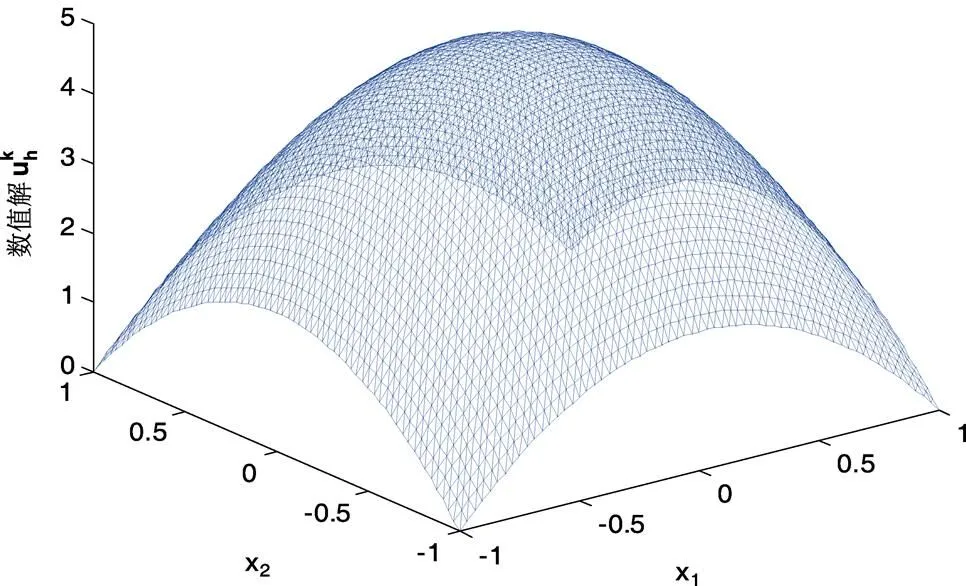
图4 算法二的的数值解图像

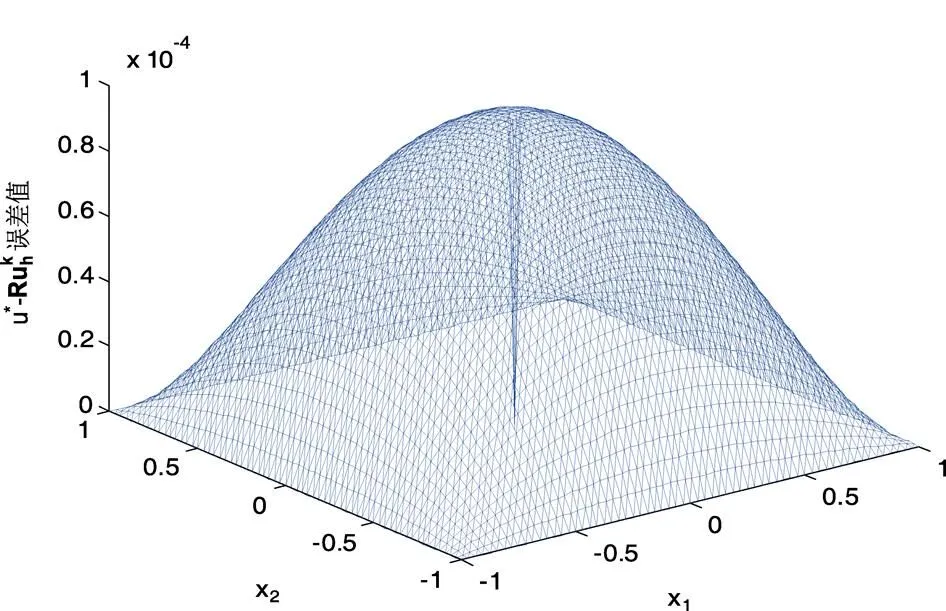
图5 算法二的的误差图像

从图6易看出算法四的收敛速率快于算法二的收敛速率，即ADMM的收敛速率要比P-D的收敛速率快。

5 结论

本论文首次尝试用P-D以及ADMM两种算法解决了由一种对流扩散方程约束的在有、无状态约束条件情况下的最优控制问题。虽然P-D和ADMM都是具有全局收敛的一阶收敛算法，但是通过数值实验可得出ADMM要比P-D算法的收敛速率快，因而证实了ADMM是一个高效的算法。

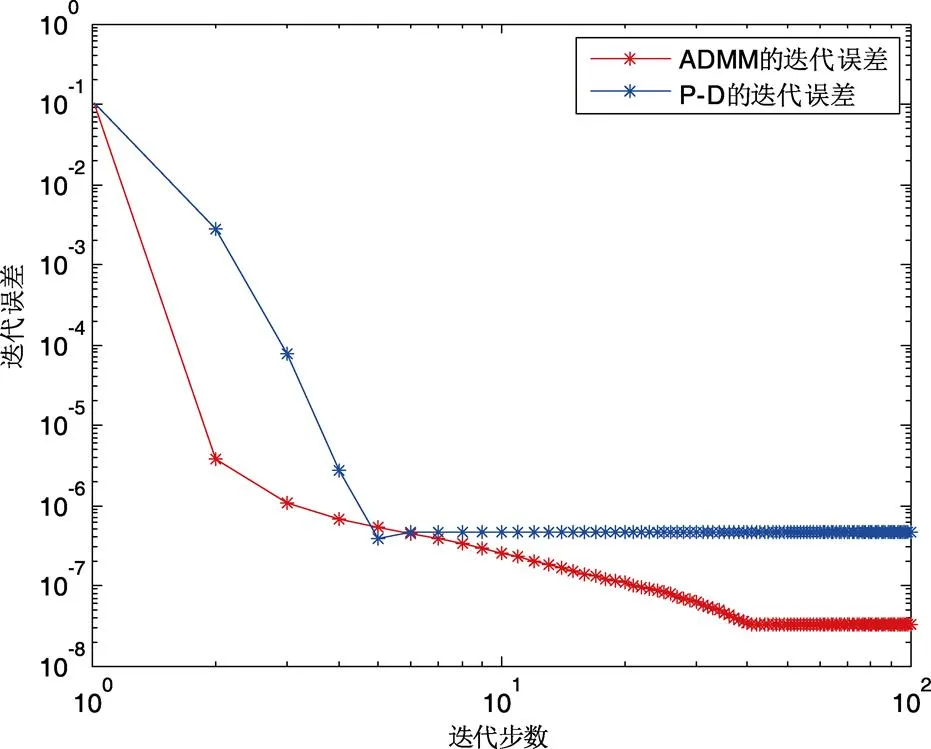
图6 算法二和算法四的收敛速率对数图像

[1] Lions J L. Optimal Control of Systems Governed by Partial Differential Equations[M].Springer-Verlag, New York-Berlin, 1971, 79.

[2] GUNZBURGER M D. Perspectives in Flow Control and Optimization[J]. Applied Mechanics Reviews, 2003, 56(6): B82-B83.

[3] KUNISCH K, WACHSMUTH D. Sufficient optimality conditions and semi-smooth Newton methods for optimal control of stationary variational inequalities[J]. ESAIM: Control, Optimisation and Calculus of Variations, 2012, 18(02): 520-547.

[4] BERGOUNIOUX M. Optimal Control of Problems Governed by Abstract Elliptic Variational Inequalities with State Constraints[J]. Siam Journal on Control & Optimization, 1998, 36(1): 273-289.

[5] 陈小翠, 张小峰. 求解一维对流扩散方程的一种新方法[J]. 武汉大学学报, 2014, 43(1): 10-13.

[6] IVANON M.Exact solutions of diffusion-convection equations[J].Dynamics of PDE,2008,5(2):139-171.

[7] REES T, DOLLAR H S,WATHEN A J. Optimal solvers for PDE-Constrained Optimization[J]. Siam Journal on Scientific Computing, 2010, 32(1): 271-298.

[8] EVANS L C. Partial Differential Equations[M]. Providence: Amer Math Soc, 2008.

[9] REYES J C D L. Numerical PDE-Constrained Optimization[M]. Springer International Publishing, 2001, 19(7): 121-163.

[10] 王烈衡, 许学军. 有限元方法的数学基础[M]. 科学出版社, 2007, 60-65.

[11] HEINKENSCHLOSS M. Numerical solution of implicitly constrained optimization problems[R]. Technical Report TR08-08, USA: Rise University, 1892, 1-22.

[12] ZHANG K, LI J S, SONG Y C, et al. An alternating direction method of multipliers for elliptic equation constrained optimization problem[J]. Science China Mathematics, 2017, 60(2): 1-18.

[13] 陈宝林. 最优化理论与算法[M]. 清华大学出版社, 2005, 33-40.

[14] HE B S, YUAN X M. On non-ergodic convergence rate of Douglas-Rachford alternating direction method of multipliers[J]. Numerische Mathematik, 2015, 130(3): 567-577

[15] BOYD S, PARIKH N, CHU E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations and Trends in Machine Learning.

Numerical Research on Constrained Optimization Problems Governed By Elliptic Equations

GAO Xin, YUAN Jian-hua

(Beijing University of Posts and Telecommunications, Beijing 100876, China)

In this paper, the primal-dual (P-D) methods and the alternating direction method of multipliers (ADMM) for solving the state constrained optimization problems, which is governed by elliptic equations, are investigated. The governing equations discussed is a kind of diffusion-convection equations. The unconstrained as well as box-constrained cases of the diffusion-convection equation control problems are solved in this work. The existence and uniqueness of the solution of the optimal control model is given, and the first-order optimality conditions is also mentioned firstly. Then the original optimal control problem can be converted into an optimized discrete system by using finite element methods. We solve the discrete optimization system by using P-D method and ADMM. The ADMM is a first order algorithm that has both the decomposability of the dual rise method and the global convergence of the multiplier method, while the P-D method is a first order algorithm with global convergence also. The purpose of this paper is to compare the primal-dual method with ADMM about the convergence rate. The numerical experiments in this paper are shown that the convergence rate of the ADMM is faster than P-D method, which means ADMM is an efficient optimization algorithm for the elliptic PDE-constrained optimization problems.

Optimal control problems; Elliptic equation constrained; Alternating direction method of multipliers; Primal-dual algorithm; Finite element method

O232

A

10.3969/j.issn.1003-6970.2018.07.012

国家自然科学基金项目(11671052, 11471052)；国家自然科学基金重大研究计划(91630202)

高新(1993-)，女，研究生，PDE最优控制。

袁健华(1979-)，教授，主要研究方向：有限元方法，微分方程数值解，最优化算法。

本文著录格式：高新，袁健华. 椭圆方程最优控制问题的数值算法研究[J]. 软件，2018，39（7）：57-62