强赋值幺半群上的加权Mealy机与加权Moore机的关系*

王 敏，李永明

陕西师范大学 计算机科学学院，西安 710119

1 引言

加权自动机[1-6]是对经典自动机[7-8]的推广，是转移上附加权重的自动机。这些权重作成的代数结构通常是半环，Droste教授等在文献[3]中已经很好地研究了取值于半环的加权有穷自动机的理论及其实际应用。2011年Droste教授在文献[4]中首次提出赋值幺半群的概念，将半环推广到更一般的赋值幺半群上，并在文献[5]中对取值于赋值幺半群的加权自动机和加权单体二阶逻辑进行详细的阐述。对一个输入字符串，不带输出的有穷自动机只判定此串是或者不是句子，这在许多时候是不够的，原因是有时不仅希望系统能得出一个输入串是否为要求串的结论，更希望系统在处理此串的过程中给出系统的输出结果。Moore机和Mealy机就是两种不同的带有输出的有穷自动机[7]。并且由于带输出的加权有穷自动机是自动机理论的一个重要研究方向，在自然语言的处理方面[9-11]有着很重要的意义。文献[12]和文献[13]分别在格序幺半群和分配格意义下，证明了格值序列机与格值Moore机是等价的，格值序列机与格值Mealy机是不等价的（包括格序幺半群取{0,1}时的情况）。从而得到了格值Mealy机与格值Moore机是不等价的。但格值序列机与格值Moore机的等价性成立是依赖于分配律的。文献[14]和文献[15]在强双半群-伪半环意义下研究伪加权序列机、伪加权Mealy机以及伪加权Moore机的关系，得到了类似的结论，且结论成立不依赖于分配律，但伪半环和格序幺半群都满足结合律。

本文在赋值幺半群的基础上引入了新的概念—强赋值幺半群，并研究了取值于新的代数结构的强赋值加权序列机、强赋值加权Mealy机以及强赋值加权Moore机的关系，证明了强赋值加权序列机与强赋值加权Moore机是等价的，强赋值加权序列机与强赋值加权Mealy机是不等价的，从而得到了强赋值加权Mealy机与强赋值加权Moore机是不等价的，且上述结论成立既不依赖于分配律，强赋值幺半群也不需要满足结合律。

2 预备知识

为了便于本文阅读，现将与本文相关的概念介绍如下。

定义1[7]Mealy机是一个六元组：

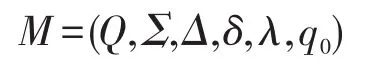
其中，Q表示状态的非空有穷集合；Σ表示输入字母表；Δ表示输出字母表；δ表示状态转移函数，有时又叫作状态转换函数或者移动函数，δ:Q×Σ→Q。∀(q,a)∈Q×Σ，δ(q,a)=p表示M在状态q读入字符a，将状态变成p，并将读头向右移动一个带方格而指向输入字符串的下一个字符；λ表示输出函数，λ:Q×Σ→Δ。∀(q,a)∈Q×Σ，λ(q,a)=d表示M在状态q读入字符a时输出d；q0表示M的开始状态，也可叫作初始状态或者启动状态，q0∈Q。

显然，∀a1a2…an∈Σ∗,M的输出串为：λ(q0,a1)λ(δ(q0,a1),a2)…λ(δ(…δ(δ(q0,a1),a2)…),an), 设δ(q0,a1)=q1,δ(q1,a2)=q2,…,δ(qn-1,an)=qn,则M的输出可以表示成λ(q0,a1)λ(q1,a2)…λ(qn-1,an),这是一个长度为n的串。

定义2[7]Moore机是一个六元组：

其中，Q,Σ,Δ,δ,q0的意义同Mealy机。λ表示输出函数，λ:Q→Δ。∀q∈Q,λ(q)=a表示M在状态q时输出a。

显然，∀a1a2…an∈Σ∗,M的输出串为：λ(q0)λ(δ(q0,a1))…λ(δ((…δ(δ(q0,a1),a2)…),an)),设δ(q0,a1)=q1,δ(q1,a2)=q2,…,δ(qn-1,an)=qn,则M的输出可以表示成λ(q0)λ(q1)λ(q2)…λ(qn),这是一个长度为n+1的串。

定义3[4]设D是一个非空集合，(D,+,0)是一个可交换的幺半群，定义D上的赋值函数val:D+→D,若赋值函数满足：

（1）∀d∈D,val(d)=d;

（2）若存在i∈{1,2,…,n},使得di=0,则val(d1,d2,…,dn)=0 。

则称D为赋值幺半群，记为(D,+,val,0)。

文中出现的∨与max表示相同意义，N表示自然数集，R表示实数集，并且用ε表示空字符串。

3 强赋值幺半群

定义4设D是一个非空集合，(D,+,val,0)是一个赋值幺半群，若赋值函数val:D+→D满足，对任意自然数k：

（1）val作用于2k个元时，

（2）val作用于2k+1个元时，

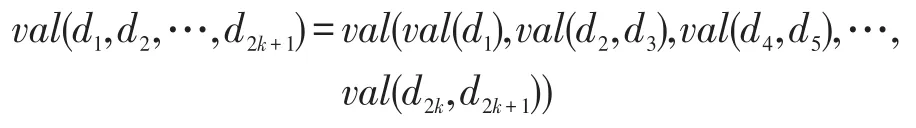
（3）存在元素e∈D，使得val(d,e)=d,∀d∈D。

则称D为强赋值幺半群，记为(D,+,val,0,e)。

例1以下代数结构为强赋值幺半群，并且赋值函数val满足结合律。

（1）D=(ℕ,+,×,0,1),D=(R,+,×,0,1)。

（2）D=(R+⋃{∞},+,∧,0,∞)，其中R+={a∈R|a≥ 0}。

注1强赋值幺半群是伪半环的推广，同时也是格序幺半群的推广。进而，本文的结果可以看作文献[12]和文献[14]的进一步推广。

通过下面的例子来说明强赋值幺半群比伪半环与格序幺半群条件弱。

例2设D=([0,1],max,val,0,1)，赋值函数val定义如下：∀x1,x2,…,xi∈[0,1],i∈N ：

可以验证D=([0,1],max,val,0,1)是强赋值幺半群，但赋值函数val不满足结合律。

4 强赋值加权Mealy机与强赋值加权Moore机及其响应函数

定义5一个强赋值加权序列机是一个五元组M=(X,U,Y,f,I)，其中，X为非空有限状态集合；U为有限输入字符集；Y为有限输出字符集；I：X→D为X上的D-值子集，表示D-值初始状态；f:X×U×X×Y→D是D-值输入-转移-输出函数，且f满足条件：

f(x,u,x′,y)表示在状态x下，输入u，到达状态x′并输出y的权重。

下面定义M的响应函数（也称为输入输出函数）为φM:U*×Y*→D,∀θ∈U*,w∈Y*,若|θ|=|w|时，设θ=u1u2…uk,w=y1y2…yk,

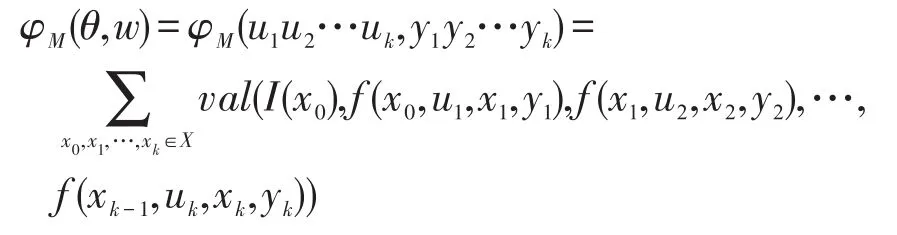
特别地，若θ=w=ε时，则若时，则φM(θ,w)=0 。

定义6一个强赋值加权Mealy机是一个六元组M=(X,U,Y,δ,h,I)，其中X、U、Y、I的定义同定义5；δ:X×U×X→D是D-值状态转移函数；h:X×U×Y→D是D-值转移输出函数，且满足条件：

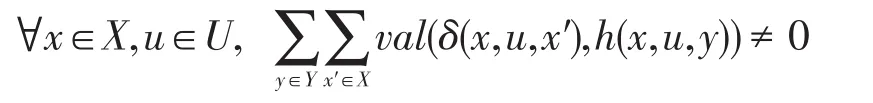
定义M的响应函数为φM:U*×Y*→D，∀θ∈U*，w∈Y*，θ=u1u2…uk,w=y1y2…yk，

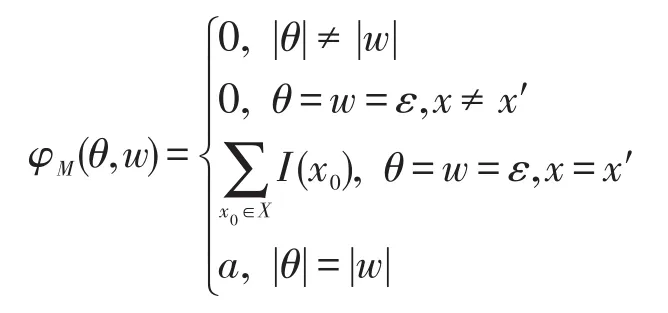
定义7一个强赋值加权Moore机是一个六元组M=(X,U,Y,δ,h,I)，其中X、U、Y、I的定义同定义5；δ:X×U×X→D是D-值 状 态 转 移 函 数 ；h:X×Y→D是D-值状态输出函数，且满足如下条件：

定义M的响应函数为φM:U*×Y*→D,∀θ∈U*,w∈Y*,

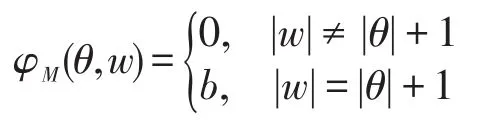
其中，当 |w|=|θ|+1 时，设θ=u1u2…uk,w=y0y1…yk,则

特别地，若θ=ε,w=y0时，φM(θ,w)=φM(ε,y0)=

接下来研究强赋值加权序列机与强赋值加权Mealy机的关系。

若强赋值加权序列机M1与强赋值加权Mealy机M2的响应函数相等，即φM1=φM2,则称二者等价，也即∀θ∈U*,w∈Y*,φM1(θ,w)=φM2(θ,w)。

定理1对任意的强赋值加权Mealy机M1，总存在与之等价的强赋值加权序列机M2。

证明任给一个强赋值加权Mealy机M1=(X,U,Y,δ,h,I)，构造M2=(X,U,Y,f,I)如下：

即∀x∈X,u∈U,上述定义的f满足强赋值加权序列机中的条件。

因此，M2=(X,U,Y,f,I)是强赋值加权序列机。

∀(θ,w)∈U*×Y*，当 |θ|=|w|时，设θ=u1u2…uk,w=y1y2…yk,

本研究考察了不同检测波长、不同柱温、不同流速以及不同流动相的样品色谱图，根据谱图分离情况确定色谱条件，具体条件见“2.1”项下。

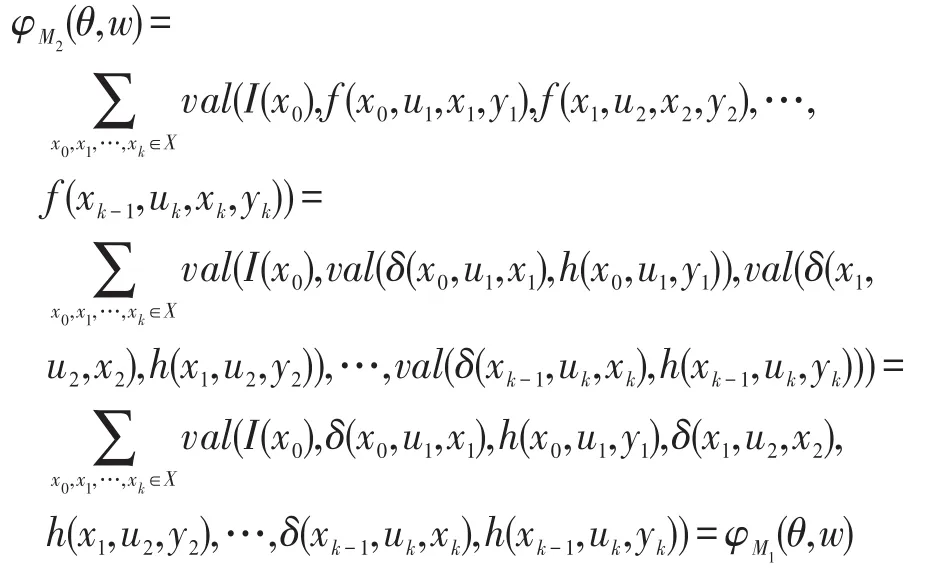
当 |θ|≠ |w|时，φM2(θ,w)=φM1(θ,w)=0 。

因此，∀(θ,w)∈U*×Y*，都有φM2(θ,w)=φM1(θ,w)。□

注2反之，任意的强赋值加权序列机，未必存在与之等价的强赋值加权Mealy机。特别地，当D={0,1}时，任给一个强赋值序列机，也未必存在与之等价的强赋值加权Mealy机，文献[12]中引理2.1及例2.2对此进行了详细的证明。

推论1强赋值加权Mealy机与强赋值加权序列机是不等价的。

5 强赋值加权Mealy机与强赋值加权Moore机的关系

下面研究强赋值加权序列机与强赋值加权Moore机的关系。

首先定义机器等价的概念。考虑强赋值加权序列机M1与强赋值加权Moore机M2，假设其具有相同的输入集合U和输出集合Y，且响应函数满足如下的关系式：则称强赋值加权序列机M1与强赋值加权Moore机M2等价。即可通过验证是否满足上述定义中的关系式来判断强赋值加权序列机与强赋值加权Moore机是否等价。

定理2对任意的强赋值加权序列机M1，总存在与之等价的强赋值加权Moore机M2。

证明任给一个强赋值加权序列机M1=(X,U,Y,f,I),构造M2=(X′,U,Y,δ,h,I′)如下：

因此，M2=(X′,U,Y,δ,h,I′)是强赋值加权Moore机。

这时，M2的响应函数计算如下：

设X′=X×Y={(x0,y′0),(x1,y′1),…,(xk,yk′)}={x0′,x1′,…,xk′}，其中：x0′=(x0,y0′),x1′=(x1,y1′),…,xk′=(xk,yk′)。

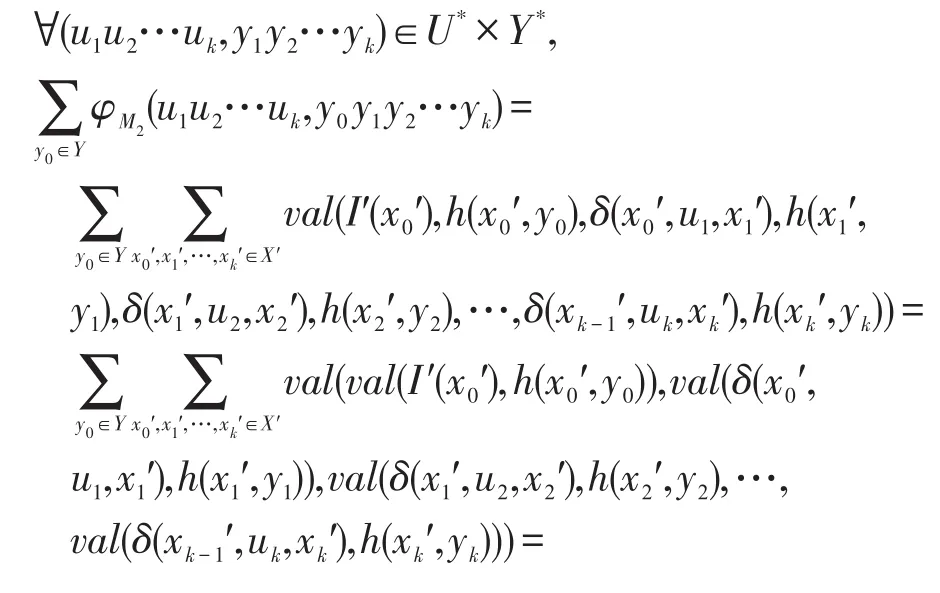
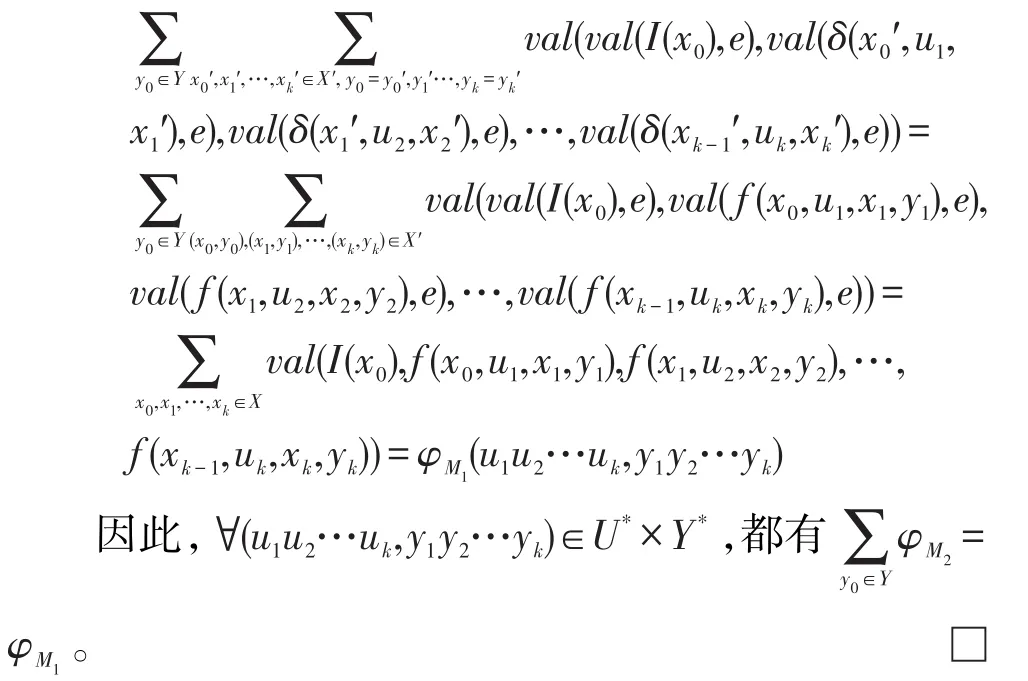
下面的例子说明了定理2中转换函数的构造。

例3设D=([0,1],max,val,0,1)是例2中定义的强赋值幺半群，X={x1,x2},U=Y={0,1}，f由如下矩阵描述：

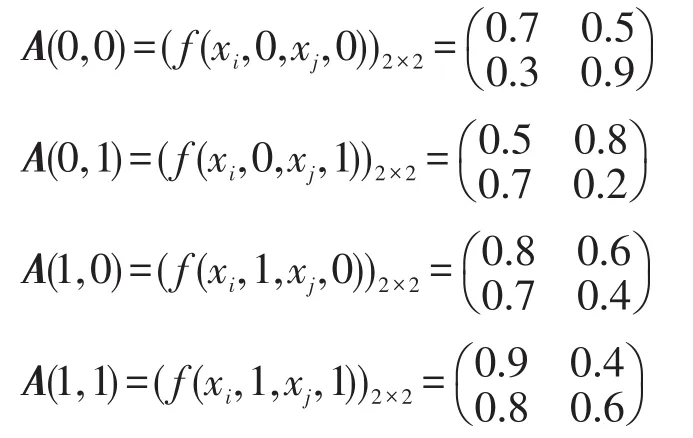
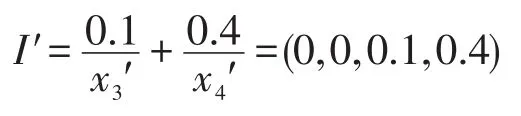
这时M与M′等价。

以θ=01,w=10为例，可得：

因此，φ′(01,110)∨φ′(01,010)=φ(01,10)。

定理3对任意的强赋值加权Moore机M1，总存在与之等价的强赋值加权序列机M2。

证明任给一个强赋值加权Moore机M1=(X,U,Y,δ,h,I),构造M2=(X′,U,Y,f,I′)如下：

即∀(x,y)∈X′,u∈U，上述定义的f满足强赋值加权序列机中的条件。

因此，M2=(X′,U,Y,f,I′)是强赋值加权序列机。

这时，M2的响应函数计算如下：

设X′=X×Y={(x0,y0′),(x1,y1′),…,(xk,yk′)}={x0′,x1′,…,xk′}，其中x0′=(x0,y0′),x1′=(x1,y1′),…,xk′=(xk,yk′)。

下面的例子说明了定理3中转换函数的构造。

例4设D=([0,1],max,val,0,1)是例2中定义的强赋值幺半群，X={x1,x2},U=Y={0,1},δ与h由如下矩阵描述：

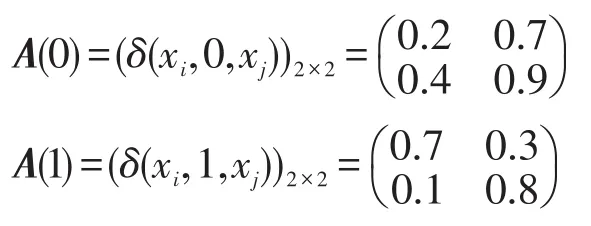
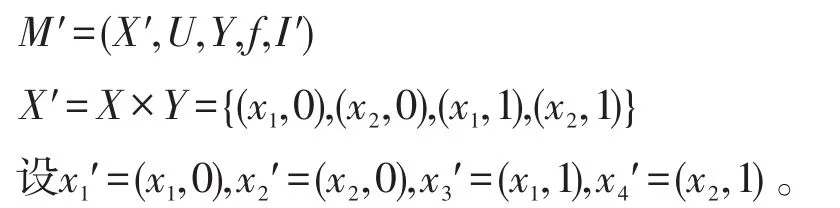
这时M与M′等价。

以θ=01,w=10为例，可得：

定理4强赋值加权序列机和强赋值加权Moore机是等价的。

由定理4和推论1可得推论2。

推论2强赋值加权Mealy机和强赋值加权Moore机是不等价的。

6 总结

本文在权重取值于强赋值幺半群下定义了强赋值加权序列机、强赋值加权Mealy机和强赋值加权Moore机，得到了强赋值加权序列机与强赋值加权Mealy机是不等价的，证明了强赋值加权序列机与强赋值加权Moore机是等价的，并以强赋值加权序列机为中介，得到了强赋值加权Mealy机和强赋值加权Moore机是不等价的。进一步将考虑权重取值于一般的赋值幺半群，以上结论是否也成立。