建立数学模型思想，提升问题解决能力——以初中数学线段和的最值问题为例

☉江苏省苏州市相城区春申中学 周丽芳

《义务教育数学课程标准》把“获得适应社会生活和进一步发展所必需的数学的基础知识、基本技能、基本思想、基本活动经验”列为课程总目标之首，并从“从知识技能、数学思考、问题解决、情感态度”四个方面阐述了具体的内涵.由此可见，数学教学过程不仅是知识与技能的学习过程，而且是问题解决策略与数学思想方法形成的过程，还是激发学习兴趣、体验成功乐趣、养成学习习惯、形成科学态度的过程.下面结合初中数学新课程教学实践案例，以线段和的最值问题为例，仅就建立数学模型思想，提升问题解决能力的问题作初步的探讨.

一、初中数学模型思想的内涵

初中数学模型思想是指运用数学模型方法处理和解决实际问题的一种思想，它是学生体会和理解数学与现实世界联系的桥梁.建立和求解模型的基本过程包括“从现实生活或具体情境中抽象出数学问题，用数学符号建立方程、不等式、函数等表示数学问题中的数量关系和变化规律，求出结果并讨论结果的意义.”数学模型思想的学习能有效提高学生学习数学的兴趣，强化应用意识，初步形成建模学习策略.

二、模型思想在解决线段和最值问题中的应用

最值问题是初中数学的重要内容之一，也是中考的热点问题.它是一类综合性较强的问题，主要考查学生综合迁移所学知识来解决实际问题的能力.无论是代数还是平面几何，在学习中都会遇到最值问题，其中常见的就是线段和的最值问题.此类问题常可归于两类基本模型：一是几何模型，多为在存在动点或者不确定的位置关系的情况下求最值，一般有两种解题思路，一个是通过几何图形的性质实现对位置的确定；另一个是通过数量关系实现最值问题的解答.二是函数模型，常可根据已知条件，将问题转化成两个变量之间的关系，进而构造二次函数解析式，通过配方利用二次函数的对称性及增减性，确定某范围内函数的最大或最小值.

1.几何模型中的线段和最值问题

图1

图2

例1 如图1，已知正方形ABCD的边长为4，M在边DC上，且DM=1，N是对角线AC上一动点，则DN+NM的最小值是________.

分析：此题为单动点求两条线段和的最值问题.D、M是两个定点，N是AC上一动点.由正方形本身具备的轴对称性可知，点B、D关于AC对称，BN=DN，DN+NM=BN+NM，由“两点之间线段最短”（三角形的任意两边之和大于第三边）可知BN+NM≥BM.所以只要连接BM交AC于N，此时DN+MN的值最小为BM的长（如图2）.再由已知条件可知BC=4，CM=3，由勾股定理可知，BM=5，所以DN+NM的最小值是5.

本题在“将军饮马”模型中植入了正方形的背景，利用轴对称性质，将直线同侧的两条线段转化为异侧的两条线段，简化问题，求得答案.

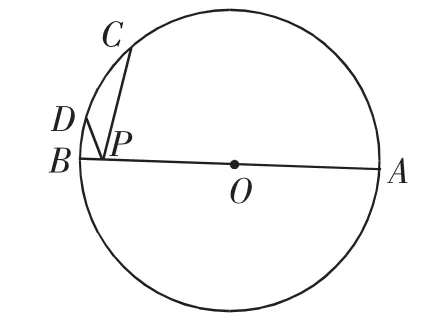
图3

图4

变式：如图3，AB是⊙O的直径，C为半圆AB上的一个四等分点，D为弧BC上的三等分点，已知⊙O半径为1，则PC+PD的最小值为________.

分析：本题由案例1变式而来，在模型中植入了圆的背景，学生只要熟悉“将军饮马”模型，就很容易作出如图4中的辅助线，得出PC+PD的最小值为线段CD′的长.根据圆的相关性质及轴对称性可求得∠COD′=60°，△COD′为等边三角形，CD′=OC=1，所以PC+PD的最小值为1.

拓展：在几何模型中植入坐标背景.

如图5，已知在平面直角坐标系xOy中，点A（6，8），B（-2，y），C（x，0），且BC⊥AC.

（1）求y与x之间的函数关系式，并求出y的最大值；

（2）如图6，当y取最大值时，一条线段EF在x轴上运动，EF=2，连接AF、AB、BE，求在运动过程中四边形ABEF周长的最小值.

分析：本题（1）可过点B、A分别作BD⊥x轴，AM⊥x轴垂足为D、M，由“K”字型可知△BDC∽△CMA，由相似三角形对应边成比例易得y=-x2+x+，经配方得y=-（x-2）2+2，所以当x=2时=2.

第（2）题中已知A（6，8），当y取最大值时可得到B（-2，2），易求得AB=10，在AB、EF长度均为定值下，要求四边形ABEF的周长最小值，就可转化成求BE+AF的最小值.与案例1相比，本题不再是两定点一动点，而是E、F两动点同时移动，这是困扰学生的难点.这时可启发学生在EF的长是定值时，能否考虑将E、F两个动点转化为一个动点，从而将问题转化到“将军饮马”模型中去解决.通过讨论，引导学生得出问题解决的关键，就是将线段AF向左平移EF的长度至A′E的位置，使得A′E=AF，将求BE+AF的最小值转化成求BE+A′E的最小值（如图7）.通过两点之间的距离公式求得BE+AF=BE+A′E=A′B′=2，AB=10，EF=2，所以四边形ABEF周长的最小值为12+2.

图5

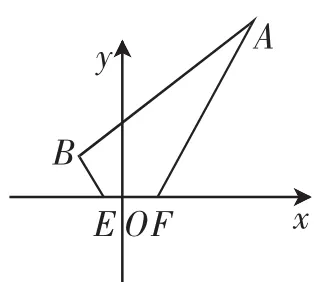
图6

图7

反思：以上求两线段和最值问题均可利用“将军饮马”模型来解决.一般都是利用轴对称性将所求线段进行转化，再根据“两点之间线段最短”来求得两条线段和的最值问题.在这种模型中植入不同的背景可以延伸出不同的题型.但万变不离其宗，其数学思考都是利用图形本身的轴对称性将同侧线段和转化为异侧线段和，即化“折”为“直”，进而引导学生能清晰地抓住求两条线段和最短问题的本质：依据“两点之间线段最短”，利用共线点最小值解决最值问题.

2.函数模型中的线段和最值问题

分析：因为点P不在直线上运动，点E也是一个动点，在无法套用“将军饮马”模型来解决问题时，我们可以利用两点之间的距离公式，将两条线段的长用函数解析式表示出来，再利用函数的性质来求线段和的最小值.具体解答如下：

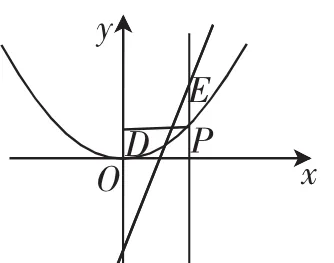
图8

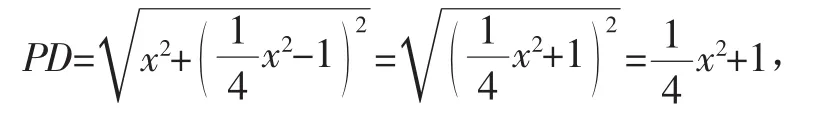
综上所述，PD+PE的最小值为2.

图9

分析：本题P、D、Q三点随点M的运动而运动，同样无法套用“将军饮马”模型来解决.这时可引导学生将线段PD、DQ的长度用含x的代数式来表示，通过构造函数解析式来解决问题.具体解答如下：

所以A（4，0），C（0，-3），

所以OA=4，OC=3，AC=5.

因为∠AOC=90°，DQ⊥AC，

反思：利用函数模型解决线段和的问题，在初中数学中，一般都是将问题转化成二次函数解析式，通过配方求得线段和的最大或最小值.方法虽比较简单，但计算一般都较繁杂.且这类问题一般都出现在综合题中，将线段长用解析式表示出来是一个难点，但只要学生有扎实的基础理论知识，理解并熟知简单数学模型的特性，把握数学思想（如化归思想、转化思想等）的本质，化繁为简，化动为定，结合特定图形的性质就能够顺利解决问题.

总之，初中数学最值问题看似复杂多变，但其中都蕴含着基础的模型思想.解这类题目的关键是要结合题意，借助相关的概念、图形的性质，通过一定的方法和手段，把几何和函数中的最值问题转化为基本的模型来解决.教师要从学生的数学实际出发，联系学生的外部世界精心创设问题情境，引导学生在建立和求解数学模型中，积累数学活动经验，建立数学模型思想，提升问题解决能力.