混合Legendre-球面调和谱方法数值求解Navier-Stokes方程

宋 洋,黄 伟

(上海大学理学院,上海200444)

在研究某些实际问题时,往往需要考虑两同心球所介区域内偏微分方程模型的数值求解.例如气象科学、海洋科学、地球物理和天体物理等领域,研究某些问题时常需要数值模拟流体在球形区域内的运动,而这类问题可转化为球形区域内偏微分方程的数值求解[1-2].随着计算机技术的飞速发展,作为求解偏微分方程的数值方法之一的谱方法越来越受到人们的重视.谱方法的突出优点是高精度.因此,本工作采用谱方法数值求解两同心球所介区域内的偏微分方程问题.

20世纪90年代,Cao等[3]和Guo等[4-5]发展了以球面调和函数为基函数的正交逼近方法,并应用于求解球面上的涡度方程和低马赫流动方程等.这奠定了球面上谱方法的数学基础,也为进一步研究两个同心球所介区域的问题提供了思路和手段.Guo等[6]和黄伟等[7]通过Jacobi谱方法和球面调和谱方法的结合解决了单位球内Navier-Stokes方程的数值求解问题.夏文杰等[8]和邓红梅等[9]分别将混合Legendre-球面调和谱方法和混合Legendre-球面调和拟谱方法应用于两同心球所介区域上Fisher型方程的数值求解.

Navier-Stokes方程在研究不可压缩流体运动中起着重要的作用.目前,已有许多算法用于Navier-Stokes方程的数值求解[6-7,10-18]本工作主要研究三维空间中两同心球所介区域内采用混合Legendre-球面调和谱方法数值求解Navier-Stokes方程的初边值问题.

式中,U(r,λ,θ,t),P(r,λ,θ,t),f(r,λ,θ,t),U0(r,λ,θ)分别表示速度、压力和密度之比、源项和初始速度,ν＞0为动力黏性系数,常数T＞0.

利用谱方法求解Navier-Stokes方程时,找到满足散度为0的正交基难度较大.为避免构造散度自由的基函数的困难,文献[6-7]在构造数值求解单位球内Navier-Stokes方程的混合谱格式时,将不可压缩条件∇·U=0用人工压缩方程

代替.尽管人工压缩条件的引入会增加一个O(ε)阶的逼近误差,但能避免构造散度自由的基函数,也不需要通常在投影方法中附加的非物理边界条件

与文献[8]相比较,本工作所面对的问题更复杂,其中方程的形式从数量方程变为向量方程,而且方程中主要的非线性项由U(U−1)变为(U·∇)U.算法的实现中涉及非线性项的处理往往占用主要的计算资源,如果说前者的处理比较直接,那么后者就需要考虑在内存和时间受到一定限制的条件下,如何平衡数组的大小与计算重复度的关系.本工作在具体的程序中较好地解决了这个问题.另外,由于空间自变量选择了更适合区域形状的球面坐标形式,动量方程中的速度应按球面坐标进行分解,但是这种情况下对应的3个分量方程形式上存在较大的差异,无论是数值分析还是实际计算都会面临不小的挑战.为了解决上述问题,本工作采用速度的笛卡尔分解,使3个分量方程在形式上保持大部分的相似,而在相应的程序设计上,则通过两种坐标系之间要素的转换来匹配梯度和散度在运算中出现的形式.

1 全离散混合谱格式

本工作以不可压缩条件被人工压缩条件(见式(2))替换后形成的方程形式为基础给出相应的全离散混合Legendre-球面调和谱格式.为了方便描述,首先引入一些必要的记号.

令 χ(r)=r2,空间={v|v在 Ω 上可测,且＜ ∞}具有下列的内积和范数：

考虑相关的正交投影.令M 和N为非负整数,PM(I)表示所有次数不超过M 的代数多项式在I上的限制所组成的集合,特别地,WN(S)表示由中所有实值函数组成的子集.令

基于简化实际计算和数值分析的角度考虑,空间自变量用球面坐标表示,速度向量按笛卡尔坐标分解,即采用混合坐标的处理方式.

若记ej为xj方向上的单位向量,v(j)表示向量函数在xj方向上的投影,那么相应地,向量函数空间内积正交投影

下面构造全离散混合谱格式.为描述方便,令

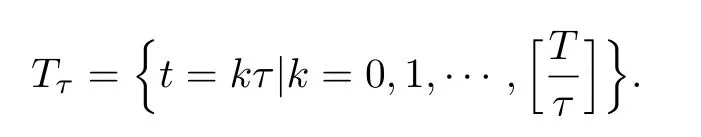
令τ表示时间t方向上的步长,则在构造格式时,需要3个参数σ1,σ2,σ3,且满足0≤σ1,σ2,σ3≤1.若记

则求解人工压缩条件下Navier-Stokes方程的全离散混合Legendre-球面调和谱格式就转换为求使对一切满足如下等式

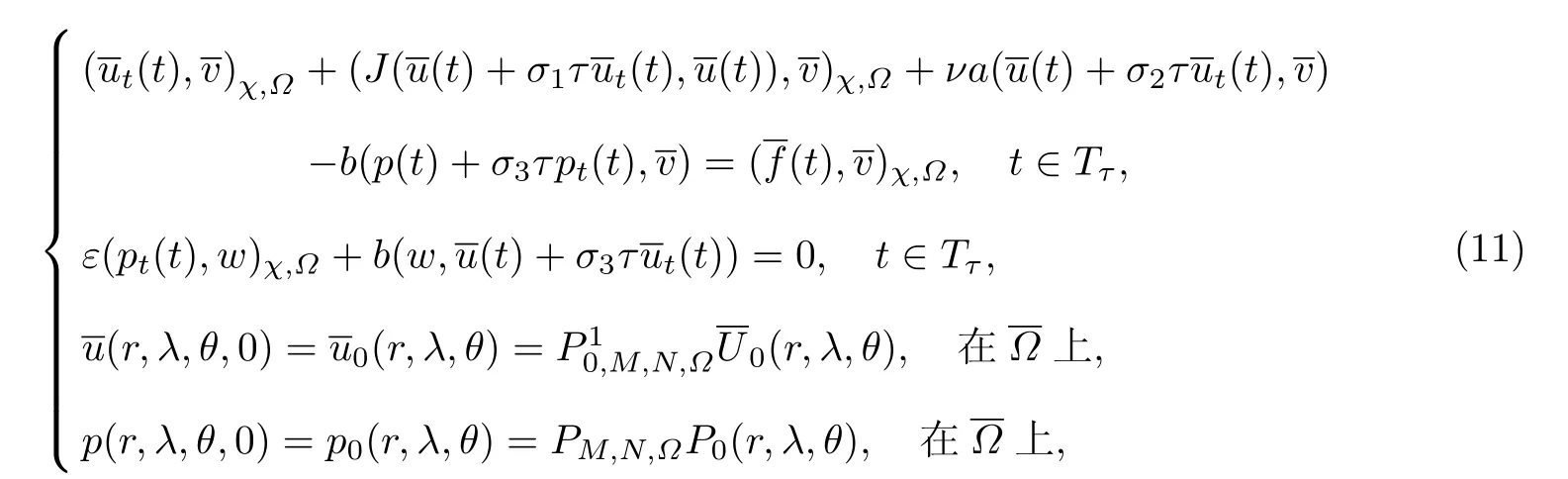
当σ1=σ2=σ3=0时,式(11)是显格式;否则,在每个时间层上和p的值由线性方程组确定.特别地,取和w为所在子空间的基函数,则该格式转化为用基函数的组合形式表达和p时的组合系数所满足的线性方程组.在实际计算中,选择球面调和函数的实部和虚部作为WN(S)的基函数,以此取代球面调和函数.这样不仅避免了复数运算,节省了内存和时间,而且在精度要求比较高的情况下为双精度型变量的引入创造了条件.

2 数值结果

对参数σ1=0,σ2=σ3=1情况下的式(11)进行数值实验,并选取试验函数

(x1,x2,x3)T与(r,λ,θ)T满足如下关系:

为了确保数值误差、初始定解条件和右端项展开式系数的计算精确度,利用Gauss型求积公式,其中和并分别用和表示的零点和相应的Christoffel数.此外,令

图1表示ν=10−4,ε=10−7和τ=τj时速度和压力的相对误差在t=1时随M,N,τ的变化.由图1可以看出:即使在M和N很小的情况下,数值结果也有较高的精度;当τ减小或M=N增加时,数值计算的误差快速递减.

通过变化小参数ε,比较t=1,M=N=7,ν=10−4及τ=2×10−4时的数值误差EM,N,u(t)和EM,N,p(t),结果如图2所示.由图2可以发现,对极大或极小的ε,数值精度可能会降低.这与文献[7]中的结论一致,即当ε与τ同阶时,可以得到较好的收敛速度.

图1 速度和压力的相对误差随M,N和τ的变化Fig.1 Relative errors of velocity and pressure varies with M,N and τ

图2 速度和压力的相对误差随ε的变化Fig.2 Relative errors of velocity and pressure varies with ε

3 结束语

本工作提出了一种求解两同心球所介区域上Navier-Stokes方程的全离散Legendre-球面调和谱方法.数值实验的结果表明,本算法具有较高的精度.另外,本算法也可应用于求解其他球形区域上的相关问题.