四面体外接球半径的常规求法
☉湖北省武汉市第四十三中学 卢 伟
近几年来,随着三视图的引入,使得立体几何客观题的考查形式趋于多样化,这其中表现突出的就是四面体外接球球心在哪里的问题.下面结合具体例题的分析,归纳,并得出结论,以期能够对这一类问题有一个较为广泛的认识.(以下例题均只求取四面体外接球的半径R)
一、定义法
球心到球面上各点的距离相等,即为半径.
下面通过对两大类型的分析,从而确定相关特征的四面体外接球球心的位置.
第一类型:“垂直+条件”型(有一条侧棱与底面垂直的四面体)
例1 在四面体S-ABC中,SA⊥平面ABC,△ABC为边长是3的正三角形,且SA=6,求R.
解析:首先找到△ABC的外心G,作OG⊥面ABC,且使得OG=SA,则满足条件的O即为该四面体外接球的球心,再取SA的中点M,连接OM,如图1所示,经计算知R=2
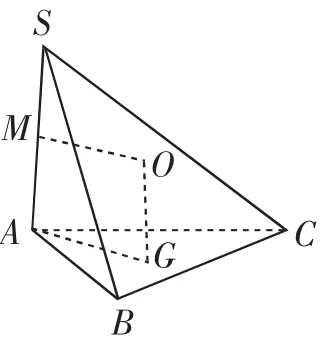
图1
例2 在四面体S-ABC中,SA⊥平面ABC,AB⊥BC,SC=2,求R.
解析:如图2,易证BC⊥SB,由直角三角形斜边的中线等于斜边的一半知SC的中点O即为球心,故R=1.(事实上,这里与例1的解题思想是一致的)
例3 在四面体S-ABC中,SA⊥平面ABC,∠BAC=120°,AB=AC=AS=2,求R.

图2
小结:这3个例题都是属于“垂直+条件”型的四面体外接球球心的问题.根据例1的作图方式我们知道,关键是先找到底面△ABC的外心,这里是分别以特殊三角形(等边三角形,直角三角形)与一般三角形(利用正弦定理)为背景,寻找突破口,则可以得到这类问题的统一计算公式.(这里r是底面三角形的外接圆半径,b为垂线段AS的长)
第二类型:“等腰+条件”型 (定义一类特殊的四面体——等腰四面体:三条侧棱相等的四面体)
例4 已知在四面体S-ABC中,SA=SB=SC=2,∠BAC=30°,BC=1,求R.
解析:我们知道等腰四面体顶点S在底面的射影是底面三角形的外心H,其外接球球心O一定在SH上,如图3所示,经计算知

图3
小结:这里对于△ABC的形状的讨论方式与类型是一致的,故可以得出统一公式(其中SA=m,r为△ABC的外接圆半径).
二、还原法
通过等价方式,将四面体的顶点还原到长(正)方体的顶点上去,从而确定其体对角线的中点即为球心.
下面再定义几类特殊的四面体:
(1)直角四面体:有共顶点的三条棱两两垂直的四面体;
(2)对等四面体:三对对角线相等的四面体;
(3)正四面体:所有棱长相等的四面体.
例5 在四面体S-ABC中,SA、SB、SC两两垂直,它们的长分别为,2,3,求R.
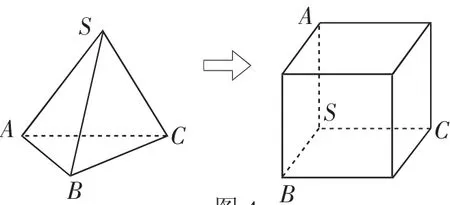
图4
小结:在四面体S-ABC中,SA、SB、SC两两垂直,它们的长分别为a,b,c,则
例6 在四面体S-ABC中,SA=BC=5,SB=AC=,SC=AB=,求R.
解析:如图5所示,结合直角四面体的处理方式.

图5
设长方体的长宽高分别为x,y,z知,

小结:在对等四面体中,SA=BC=a,SB=AC=b,SC=AB=c,则
例7 在棱长为4的正四面体S-ABC中,求R.
三、向量法
通过建系,写出相关点的空间坐标,再结合两点间的距离公式,回归定义,即可求取R.这里给出例1的向量法过程.建立如图6所示的空间直角坐标系知,A(0,0,0),BC(0,3,0),S(0,0,6).
设球心O(x,y,z),半径为R.
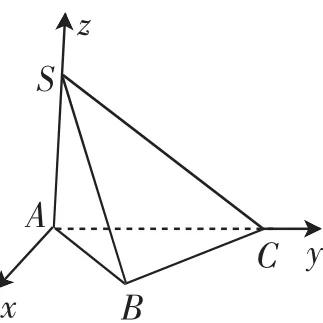
图6
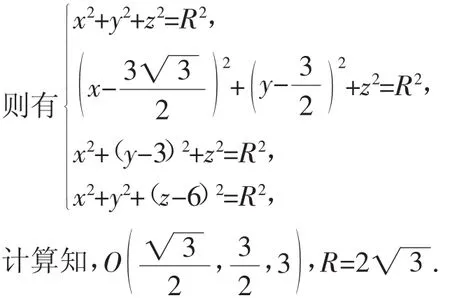
小结:向量法的过程较为直接,省去了传统的分析过程,计算量不大,但前提是要方便建系,并且能够写相关点的坐标.
综上,我们知道,关于四面体外接球球心的寻找过程是比较灵活多变的,至于方法的选用,就需要我们对已知条件进行准确的分析,合理的定位,或回归定义,或等价还原,或规范建系,只有这样,我们才能够寻找到最优的解法.F

