课堂合作，课外自学——谈初中数学课堂与课外的有机整合

江苏省常熟市实验中学 杨 军

与国外教育相比，我国教育目前的短板在于过于注重知识的传授，忽略了培养学生独立思考的能力。表态多、立场多、结论多是当前课堂教育存在的主要弊端，它所带来的直接结果是学生们接受的固化结论越来越多，逐渐就丧失了独立思考能力。一旦学生们失去这种能力就容易走进极端，要么是闭锁心智，没有了学习与生活的自理能力；要么是陷入思考的恐慌匮乏，片面追求特立独行。因此培养学生的独立思考能力是教学的关键，也应该是教育者研究的众多课题中最重要的一课。然而敏锐的思维并非与生俱来，是需要严格训练和着力培养的。众所周知，数学是锻炼学生思维的一门重要学科，在数学教学中通过课堂合作与课外自学的有机整合，对学生进行独立思考能力训练是每个数学教育者应关注的课题。本文结合初中数学教学实践，对此进行了深入思考与研究。

一、注重合作前自主预习

一般而言，选择作为合作学习的课题和内容大多数是容易引发起学生争议或者具有开放性的知识，或者是理解难度超出了大部分学生的认知水平，以及综合性强、范围广的知识。因此在进行课堂合作之前让学生们进行课前的自主预习是十分有必要的，一方面，通过预习可以对所学内容有一个提前的初步感知，在心理上与认知上都给学生提供了一个预热期和准备期；另一方面，课前预习是帮助学生养成自主认知习惯和独立思考能力的良好开端。一些很具有探索价值的知识内容，也可以在课前就让学生们开始自由结组，通过合作去进行发现探究。

如在学习《多边形内角和与外角和》时，就可以让学生们提前进行结组预习，四到五人为一组，要求每组提前画出一组不同形状的多边形和它们的外角，测量计算每个多边形外角和，再以计算结果为依据对任意多边形外角和进行猜想，尝试通过思考找到进行论证推理的方法，然后带着自己的猜想与方法进行课上交流。

而针对《全等三角形》这类涉及一些研究方法的知识内容，可通过练习题的形式让学生们进行课前自学和预习感悟：

1.概念类

找出教材中大小形状完全相同的图形，并进行记录；请再举出最少三个类似例子；按照教材中的指导方法进行操作并思考回答；你发现这些图形具有怎样的共同特征（放在一起完全相同）？那么你能得到怎样的概念？（全等）

2.性质类

按照教材方法，你制作的全等三角形重合后，对应角和对应边有怎样的关系？确定全等三角形对应角和对应边有怎样的规律，尝试进行总结。

在课上通过小组研讨课前预习中都遇到了哪些无法解决的问题？不会的通过小组解决或者向教师求教，这样课堂合作的效果就会大大提高。

二、创建课堂合作情境

开启课堂合作模式的前提条件是让学生先要产生合作意愿，这种内在情感会转化为一种内驱力，驱动学生主动寻求他人的合作与帮助，也会在合作中表现出积极的一面，这种状态无疑会成为学生们去解决、克服各种障碍，主动进击的助力。基于中学生情感的反复性与波动性比较显著的特征，激发学生这种情感与意愿，需要教师结合教材内容与目标，设置科学合理，生动融洽的数学情境。

如在讲到函数知识时，可以设置简单直接的问题情境：问题①：小A的姐姐是大学生，她想利用假期打工，某公司给出了每小时16元的薪酬条件，如果小A的姐姐一个月在该公司的工作时间是t，所得薪酬是m，那么请将下列表中数据填写完整：

t（工作时间）/小时 1 5 10 15 …… t ……m（薪酬）/元

如何用“t”的代数式表示“m”？

问题②：将物体悬挂在弹簧上，弹簧会被拉伸，悬挂物体质量与弹簧拉伸长度之间有怎样的函数关系？类似于这些具有一定操作难度，学生独立完成感觉吃力的问题情境，他们就会主动寻求同伴帮助，可以两两分工合作完成，一人进行观察，一人进行数据的记录与整理，两人合作就能够高效地解决问题。

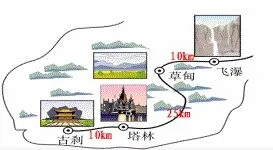
同样的函数问题，还可以给学生们创建一个生活化的数学情境：“周日，你约自己的好朋友一起去某景区游玩，景区分布图如图所示。你与朋友约好两人在飞瀑景点见面。早上七点钟你与好友同时出发，但你的出发点是古刹，交通工具是电动汽车，车速是每小时36公里；好友的出发地是塔林，交通工具是电动车，车速是每小时26公里，那么当你追上好朋友的时候，你们是不是都已经从草甸经过了？”将看似很难的函数问题转化成为一个极具现实意义与生活色彩的情境，让学生们感受到了问题的难度，但又因为熟悉的生活化场景，反而激发起了合作探究的兴趣和信心，所以课堂合作很快就顺利展开了，经过讨论后大家还列出了不同的方法：

方法1：可以将它看为一个只是不同地点同一时间两人出发到某地的纯粹的“追及问题”，所以只要求出两人何时在何地相遇，就能够判断出两人是否都从草甸经过，而这也包含着两种算法，即算术算法和方程算法。

方法2：将两人所走时间和路程看作两个存在正比例关系的变量，再运用函数知识，两人相遇的地点和时间即函数图像交点，从中又可以猜想到因为两个变量会存在在很多种设法，所以也会有不同的算法与答案。

只是一个看似简单的情境转换，不但让学生们积极开展了合作模式，还让他们在合作中绽放出异彩纷呈的思维光芒。

三、发挥“方法论”在合作中的推动作用

课堂合作学习模式并非单纯的“搭班子干活”，重要的是让学生们学会如何在合作之中发挥自己的智慧，同时也汲取他人的丰富经验，从而在和谐互动的氛围中，完成知识与能力体系的自我构建。在合作的过程中，掌握一定的解题方法与诀窍，对合作学习的顺利展开与高效率成果具有关键的推动作用，因此教师在合作学习活动的设计与组织时，应注重方法传授在整个活动中的作用，给学生们搭建起自主合作与学习的平台，并教给他们如何对问题进行不断的反思与总结，让学生们自己找到解决问题的要领和方法，提高个人和团队效能。如在学习“平行四边形的性质”的相关知识时，老师可以给出一个案例：“如图，已知ABCD是一平行四边形，F和E分别是边BC与AD的中点，求证CE=AF。”

让学生们进行合作探究，将学生们按照认知水平与能力层次不同进行组间结合，共同完成此项解答任务。完成这个任务的关键点在哪里？应从何入手进行探究解答？老师可以给学生们一个小小的提示，让他们从平行四边形的性质定理这个角度去思考。沿着这个思路，学生们很快找到了不同的解法，有的是从老师的建议去思考，从问题条件中对AECF这个四边形是平行四边形进行判定，方法如下：

证明过程：

∵四边形ABCD是平行四边形，

∴AD∥BC，AD=BC。

∵F和E分别是边BC与AD的中点，

∴四边形AECF是平行四边形，∴AF=CE。

有的小组则想到的是从判定全等三角形的角度，先证明△CDE与△ABF是否全等，然后再得出CE与AF相等的结论，证明过程如下：

∵四边形ABCD是平行四边形，

∴AB=CD，∠B=∠D，AD=BC。

∵F和E分别是边BC与AD的中点，

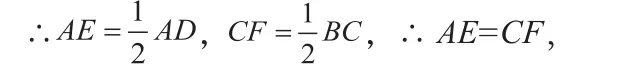
∴△ABF≌△CDE，

∴AF=CE。

传授给学生一定的方法，并鼓励他们大胆尝试不同方法，就是让学生们积累经验，又不断在经验之上寻找探究到更多更好的方法，既强调了合作学习中学生经验的共享，也突出了在合作之中学生仍旧有机会实现个性化的突破与发展，这就是老师在课堂合作学习模式中主导作用的最大发挥。

四、将合作延伸到课外

数学知识的可拓展性和延续性是很强的，一些知识内容仅凭课堂合作就让学生能够深入透彻进行理解，有时候是不现实的，尤其数学最显著的特征——应用性也无法完全在课堂得到彰显，所以将课堂合作与课外自主学习结合起来，通过一些实践性、体验性与调查性较为突出的课外合作活动设计，发展中学生数学实践应用能力，让他们在亲自收集、整理数据的过程中去感受数学的现实意义，以及数学和家庭、社会以及大自然之间存在的种种联系，从而让他们建立起数学意识，才是数学教育的本质所在。

科技发展带来的是社会更大的竞争，在这种社会现状下，合作能力成为比知识技能更重要的一项生存技能。合作能力与独立思考能力都是个人优秀品质中不可或缺的能力素质，同样也是初中数学的教育重点。通过课堂合作和课外自主学习整合，是理性化合作学习与感性化课外活动的完美结合，它与合作学习模式的本质更契合，同样也是素质教育改革背景下创新数学课堂教学的最佳选择。