基于余量谐波平衡法的质点振动系统高阶近似与频率响应分析

国忠金， 张 伟， 夏丽莉

(1. 泰山学院 数学与统计学院，山东 泰安 271000；2.北京工业大学 机电学院，北京 100124；3. 机械结构非线性振动与强度北京市重点实验室， 北京 100124)

非线性动力学与振动分析对机械、结构动力学问题研究是非常重要的，它能够全面了解和准确预测系统运动特性。近年来，旋转抛物线上的质点运动系统引起了广泛关注[1-2]，其控制方程为如下非线性自治微分方程

(1)

式中：△为线性刚性系数且△>0；q为非线性项系数且q>0；A为初始振幅且A>0。

针对方程(1)，文献[3]运用同伦与摄动耦合方法，文献[4]利用改进的迭代摄动法，文献[5]运用能量平衡法、同伦摄动法、振幅-频率公式以及微分变换法，文献[6]运用哈密尔顿法，文献[7]运用变分法，文献[8]运用优化同伦分析方法获得了其稳态下的振动频率。一方面，以上文献给出的近似振动频率与精确结果之间存在一定的误差，其近似精度有待提高。另一反面，摄动方法适用于弱非线性系统，对系统稳态下的振动频率随系统参数尤其是非线性项系数变化的振动特性还需进一步研究。

谐波平衡方法是不受小参数约束应用最广泛的定量分析方法。文献[9]应用谐波平衡法计算了一个恢复力与因变量成反比的非线性振子的近似频率和近似周期。文献[10]基于谐波平衡法研究了摆线钢球行星传动系统的基频稳态响应及动态特性。谐波平衡对于一阶近似解求解很方便，但精度不高。因此，许多研究者将谐波平衡法进行了一些推广，发展了一些诸如增量谐波平衡[11]、摄动-增量[12]、牛顿谐波平衡[13]、余量谐波平衡[14]、多层余量谐波平衡[15]等方法。余量谐波平衡引入阶层参数，融合同伦思想到谐波平衡方法中，继而余量延拓，易获得高阶近似解。

本文针对旋转抛物线上的质点运动系统构建了其振动频率、稳态响应求解的余量谐波平衡解程序，得到系统的高阶余量谐波平衡近似，并与已有文献结果进行比较分析。进而研究了系统初始振幅、非线性项系数等参数对系统非线性振动频率特性的影响。

1 余量谐波平衡解程序

假定ω是方程(1)的未知振动角频率，引入变量τ=ωt，得

(2)

基于方程(2)的对称性，其周期解具有如下基本解级数形式

{cos[(2k+1)]|k=0,1,2,…}

(3)

为方便计算，引入阶层参数p，并将系统稳态下解响应及振动频率设为

(4)

式中：ωi(i=0,1,2,…)为未知频率。

1.1 初始谐波近似

根据方程(2)初始条件，初始谐波解为如下形式

u0(τ)=Acos(τ),τ=ω0t

(5)

将式(5)代入式(2)，得初始余量项

(6)

根据伽辽金法，消除久期项，易获得初始谐波近似频率及周期响应为

(7)

式(7)近似公式与同伦与摄动耦合方法、改进的迭代摄动法、能量平衡法、同伦摄动法、振幅-频率公式、哈密尔顿解法、变分法等方法近似结果一致。

1.2 1 阶余量谐波近似

将初始近似式(7)代入余量项式(6)时，系数非零。因此，我们将式(4)代入(2)合并阶层参数的一次系数，得

(8)

式(8)为关于未知ω1和u1(τ)的线性方程，根据周期解级数形式(3)及初始条件，假定

u1(τ)=a3,1[cos(τ)-cos(3τ)]

(9)

将式(9)代入式(8)，并消除初始余量项，得

R1(τ)=Г1(τ)+R0(τ)=

(10)

将初始余量项引入式(10)，提高解的精确性。根据伽辽金法，消除久期项，我们解cos(τ)和cos(3τ)的系数方程得1-阶余量谐波近似为：

(11)

1.3 2 阶余量谐波近似

将1-阶余量谐波近似式(11)代入余量项式(10)时，cos(5τ)系数非零。因此，我们将式(4)代入式(2)合并阶层参数p的2次系数，得

(12)

式(12)为关于未知ω2和u2(τ)的线性方程，根据周期解级数形式(3)及初始条件，假定

u2(τ)=a3,2[cos(τ)-cos(3τ)]+a5,2[cos(τ)-cos(5τ)]

(13)

将式(13)代入(12)式，并消除1-阶余量项，得

(14)

根据伽辽金法，消除久期项，我们解cos(τ)，cos(3τ)和cos(5τ)的系数方程得2-阶余量谐波近似为：

(A+a3,1+a3,2+a5,2)cos(τ)-(a3,1+a3,2)cos(3τ)-

a5,2cos(5τ),τ=ω(1)t

(15)

1.4 高阶余量谐波近似

类似于上述求解过程，一般地，k-阶余量谐波近似

u(k)(τ)=u(k-1)(τ)+uk(τ),

u(k-1)(τ)=u(k-2)(τ)+uk-1(τ),

u(0)=Acos(τ),ω(0)=ω0,k=2,3,4,…

(16)

2 结果分析与讨论

本部分给出了实例讨论了文中所给出结果的有效性，并图解了非线性项系数，线性刚度系数，初始振幅-频率曲线以及初始振幅、非线性项系数的影响。

2.1 近似解析解比较

通过积分方程(1)，其精确振动频率为

(17)

表1给出了已有文献[3-7]结果与本文2-阶余量谐波近似结果的比较，其中相对误差定义为：

(18)

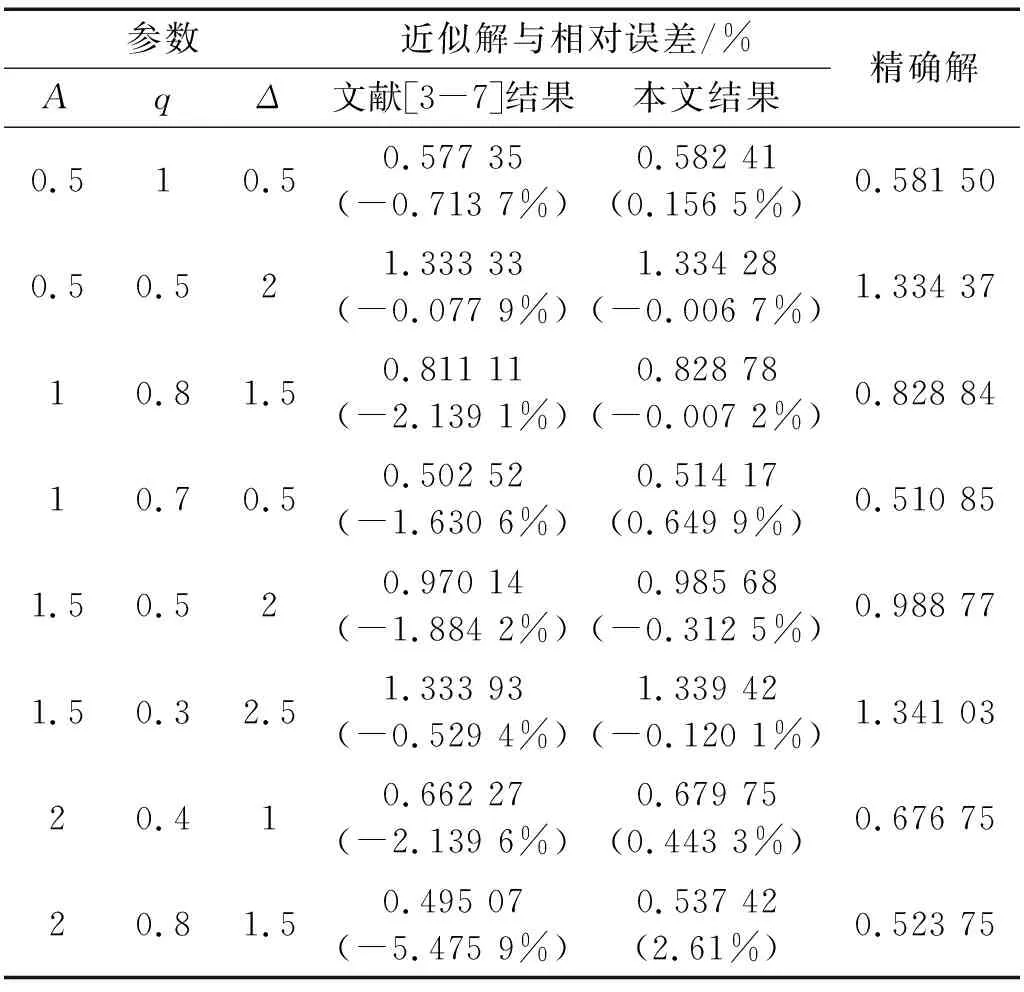
表1 余量谐波平衡解频率及其相对误差与已有文献和精确解结果的比较Tab.1 The Residue harmonic balance frequency and relative error presented here with result comparison from other references and exact solution

从表1可以看出，本文给出的近似振动频率结果比已有文献：同伦与摄动耦合方法、改进的迭代摄动法、能量平衡法、同伦摄动法、振幅-频率公式、变分法、哈密尔顿法等方法在各类参数下结果更加精确，与精确解的相对误差大大降低。

为了进一步图解本文结果的有效性，图1，2显示了不同参数下系统的时域振幅曲线比较。其中，图1近似解析表达如下：

文献[3-7]近似为：u(t)=cos(0.811 1t)

本文2-阶余量谐波平衡近似：

u(t)=1.058 7 cos(0.828 78t)-0.076 7 cos(2.486 3t)+0.017 95 cos(4.143 9t)

图2近似解析表达如下：

文献[3-7]近似为：u(t)=2 cos(0.662 27t)

本文2-阶余量谐波平衡近似：

u(t)=2.114 6 cos(0.679 75t)-0.150 2 cos(2.039 3t)+0.035 55 cos(3.398 7t)

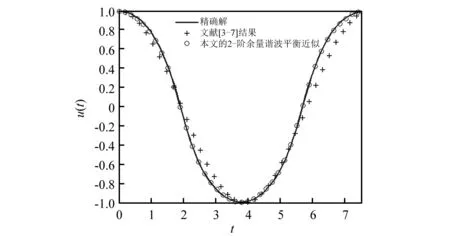
图1 解析近似解与精确解比较当q=0.8,Δ=1.5与A=1 Fig.1 Comparison of analytical solution u(t) with the exact one for case q=0.8，Δ=1.5 and A=1

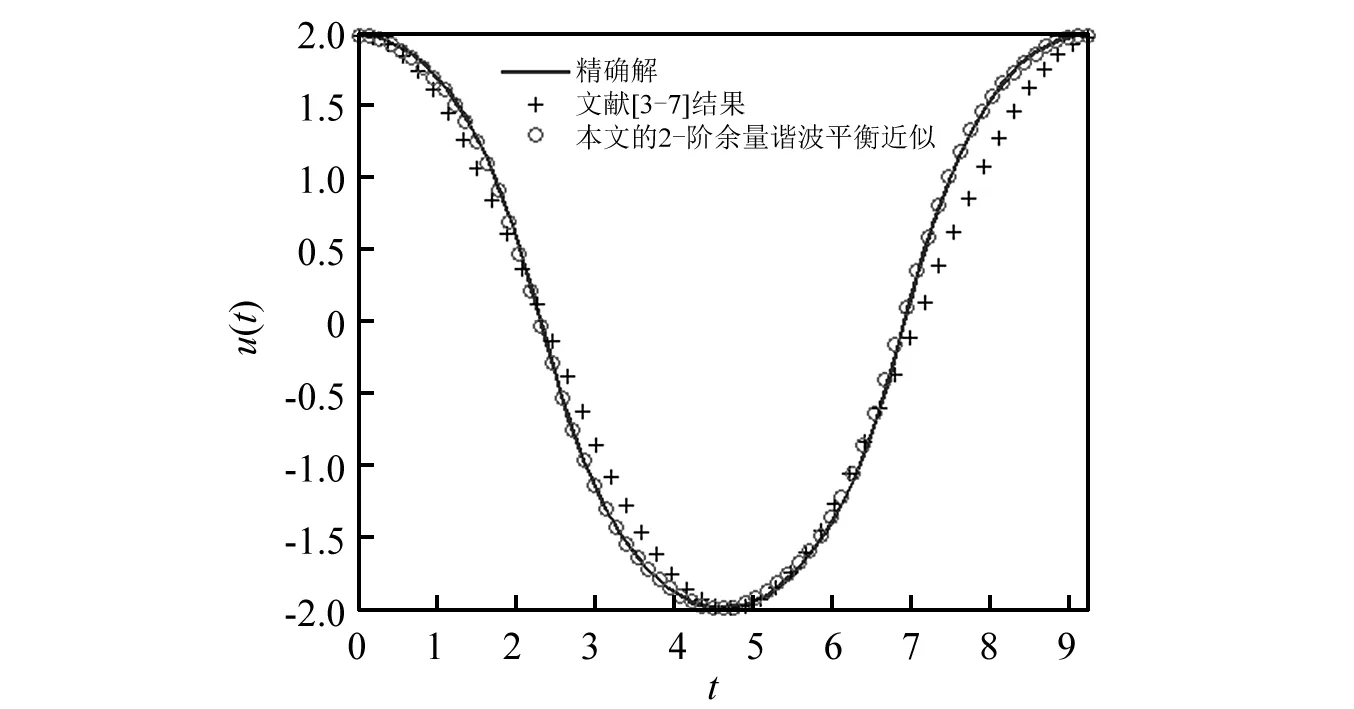
图2 解析近似解与精确解比较当q=0.4,Δ=1.5与A=2 Fig.2 Comparison of analytical solution u(t) with the exact one for case q=0.4，Δ=1 and A=2

2.2 非线性项系数q-频率曲线及其初始振幅影响

以Δ=1.5为例，图3图解了非线性项系数-振动频率曲线及其初始振幅的影响。其中圈线为本文所给出的2-阶余量谐波近似，实线为精确值。从图3可以看出，随着系统非线性项系数q的增大，振动频率逐渐减小，初始振幅越大，其相应的振动频率越小。并且本文获得的高阶解析近似结果与精确值吻合的相当好。

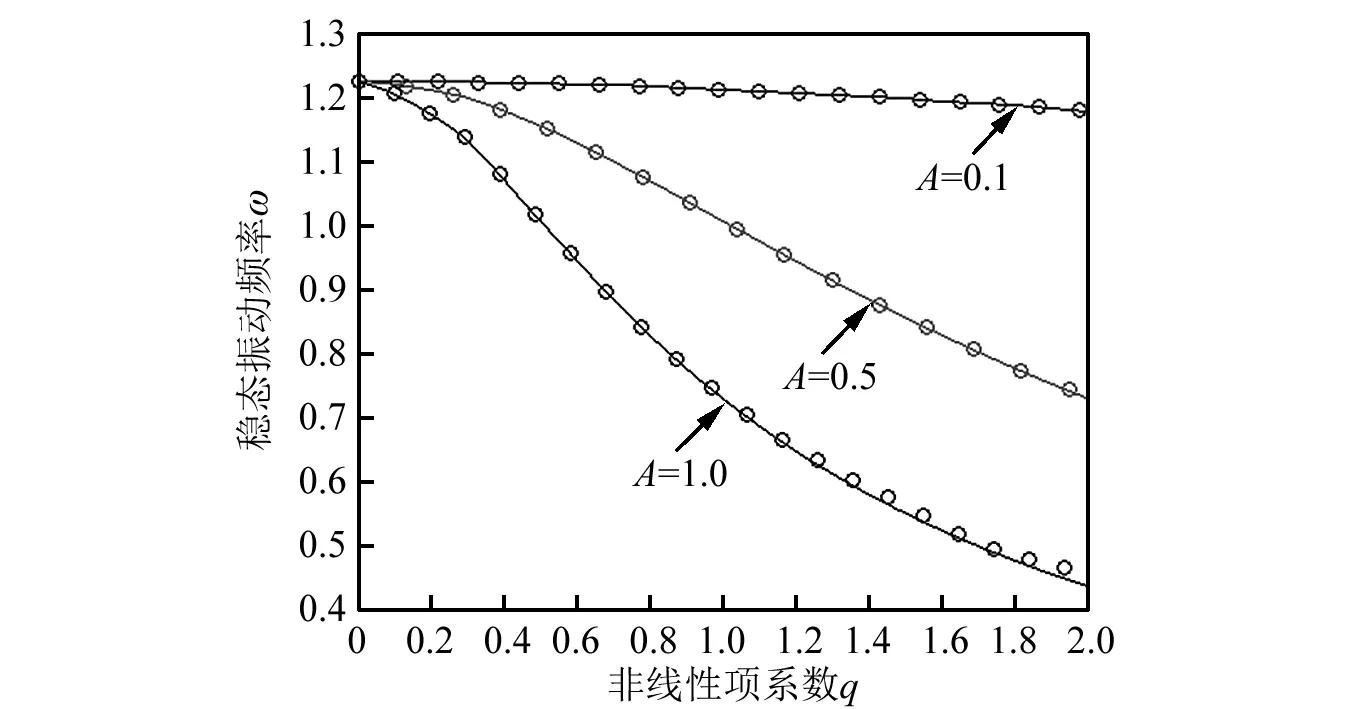
图3 非线性项系数q与振动频率曲线及其比较Δ=1.5，其中“o” 线表示本文的2-阶余量谐波平衡近似，实线为精确结果。Fig.3 Comparison of vibration frequency corresponding to nonlinear parameter q and Δ=1.5.“o” lines denotes the presented second-order residue harmonic balance approximations, solid lines are exact ones.

2.3 初始振幅A-频率曲线及其非线性项系数影响

以Δ=2为例，图4图解了初始振幅-振动频率曲线及其非线性项系数的影响。其中圈线为本文所给出的2-阶余量谐波近似，实线为精确值。从图4可以看出，随着初始振幅A的增大，振动频率逐渐减小。在其他参数不变条件下，非线性项系数越大，其相应的振动频率越小。并且本文获得的高阶解析近似结果与精确值吻合的比较一致。

图4 初始振幅A与振动频率曲线及其比较Δ=2，其中“o” 线表示本文的2-阶余量谐波平衡近似，实线为精确结果。Fig.4 Comparison of vibration frequency corresponding to initial amplitude A and Δ=2.“o” lines denotes the presented second- orderresidue harmonic balance approximations, solid lines are exact ones.

2.4 线性刚性系数-频率曲线及其非线性项系数影响

以A=0.5为例，图5图解了线性刚度系数-振动频率曲线及其非线性项系数的影响。其中圈线为本文所给出的2-阶余量谐波近似，实线为精确值。从图5可以看出，随着线性刚度系数Δ的增大，振动频率逐渐增大。在其他参数不变条件下，非线性项系数越大，其相应的振动频率越小。并且本文获得的2-阶余量谐波解析近似结果与精确值保持一致。

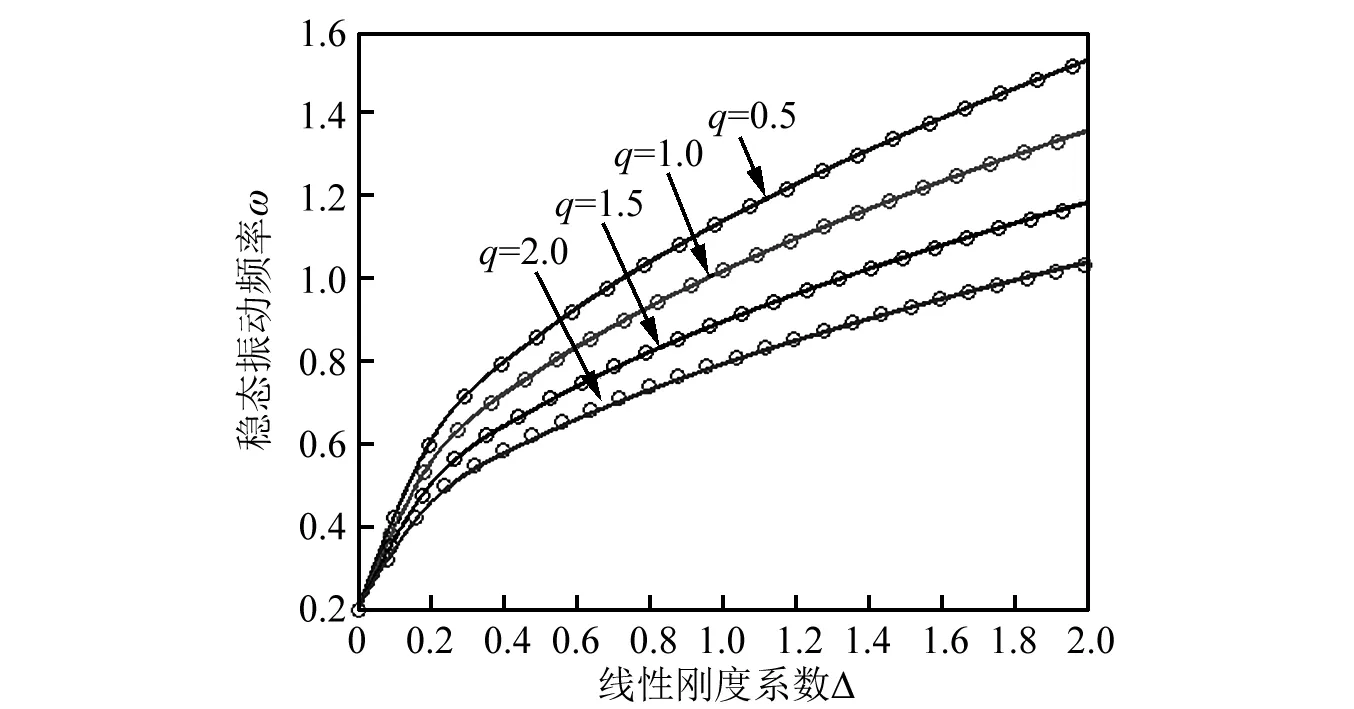
图5 线性刚度系数与振动频率曲线及其比较A=0.5，其中“o” 线表示本文的2-阶余量谐波平衡近似，实线为精确结果。Fig.5 Comparison of vibration frequency corresponding to linear stiffness coefficient Δ and A=0.5. “o” lines denotes the presented second-order residue harmonic balance approximations, solid lines are exact ones.

3 结 论

本文基于谐波平衡方法，发挥同伦思想的优势，构建了不含小参数,适用于求解非线性自治振动系统高阶近似的余量谐波平衡解程序。解程序在每一阶近似中均消除了上一阶的谐波余量，高阶近似表达仅需初始谐波近似，不需根据前一阶近似进行调整。理论上，任何精度的高阶近似均能依次获得。

将方法运用到旋转抛物线上质点运动方程中，我们可以看到

(1)本文获得的2-阶余量谐波平衡近似振动频率比已有的变分法、哈密尔顿法、同伦与摄动耦合方法等结果更加精确，与精确值的相对误差在不同参数下均大大降低。本文获得的高阶解析近似结果与精确值吻合的相当好。

(2)系统稳态下的振动频率随系统非线性项系数的增大而逐渐减小，并且初始振幅越大，其相应的振动频率越小。

(3)系统稳态下的振动频率随初始振幅A的增大而逐渐减小，并且非线性项系数越大，其相应的振动频率越小。

(4)系统稳态下的振动频率随线性刚度系数Δ的增大而逐渐增大，并且非线性项系数越大，其相应的振动频率越小。