实数连续性的一个小数表示公理及应用

刘捷，宋述刚，肖志华

(长江大学信息与数学学院，湖北 荆州 434023)

实数理论是现代分析数学的基础。在实数的公理系统中，连续性公理是一个十分重要的命题，熟知的相互等价的系列命题有确界定理、单调有界定理、闭区间套定理、有限覆盖定理、聚点定理、柯西收敛准则等。这些实数连续性命题在研究连续函数的分析性质以及相关微积分理论中，起着十分重要的作用。

公理是指不需证明而直接认为是真理的命题。在现行的《数学分析》教材中，有些是先认可一个实数的连续性公理，然后再推导出其他等价性命题，有些则是在认可了实数的十进制小数表示之后，进而证明确界定理等系列实数连续性命题[1～2]，这实际上是先认可了每一个实数都可以表示成十进制无穷小数。魏尔斯特拉斯(Weierstrass,1815～1897)就是从十进制小数表示出发建立的实数理论[3]。

宋述刚等[3]曾给出了实数连续性的一个新的等价命题：实数集的单调有界网必收敛。这是单调有界数列必收敛这一命题的推广。以此为基础可以刻画黎曼积分的概念与函数的可积准则。下面，笔者给出了实数连续性的一个命题——小数表示公理，并讨论了其与实数已知连续性公理的等价性。

1 小数表示公理

十进位小数是指形如:

a0.a1a2…an…

的表示，其中a0∈Z,an∈{

0,1,2,…,9

}。若a0∈N，则称为非负实数，否则称为负实数。

对于非负有尽小数：

a0.a1a2…an

其中an≠0，有以下2种无尽小数的表示：

a0.a1a2…an000…

a0.a1a2…(an-1)999…

后者称为非规范小数，前者称为规范小数。

关于无尽小数的大小顺序、有尽小数的稠密性、四则运算等参见文献[4]。

小数表示公理任意一个实数都可表示为十进无穷小数:

a0.a1a2…an…

其中a0∈Z,an∈{

0,1,2,…,9

}。此处及以下均指规范小数。

2 小数表示公理与闭区间套定理的等价性

在多种《数学分析》教材中，一般都是用小数表示公理来证明确界原理。以下笔者用闭区间套定理证明小数表示公理。

不妨设x∈[

0,1

]，将闭区间[

0,1

] 10等分，得到10个闭区间，分别为:

(1)x不落在区间等分点上。以下作同一个假设。

则取x的第一位小数为x1。

再将区间[a1,b1]10等分，所得到的10个闭区间可分别表示为：

假设x落在其中一个区间中，记x所在闭区间为[a2,b2]，则x的第2位小数可记为x2。继续不断10等分上一步所得到的x所在的闭区间，设第k次等分区间可表示为：

假设x落在其中一个区间中，记x所在闭区间为[ak,bk]，类似的取x的第k位小数为xk。将上述步骤无限进行下去，即可得到x的表示为:

x=0·x1x2…xk…

(2)x是某次的区间等分点。假设x是k次区间等分点：

当x作为前一闭区间的右端点时，记x所在闭区间为[ak,bk]，则x的第k位小数可记为xk-1。将上述步骤无限进行下去，x总是第10个小区间的右端点，即可得到x的表示为：

x=0·x1x2…(xk-1)999…

当x作为后一闭区间的左端点时，则x的第k位小数记为xk。类似可得到x的表示:

x=0·x1x2…xk000…

由于上述闭区间{

[an,bn]

}满足：

①[an,bn]⊆[an+1,bn+1]n=1,2,…

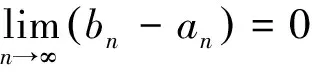
可得{

[an,bn]

}为一闭区间套。由区间套定理即可得，仅有唯一实数x，使：

x∈[an,bn]n=1,2,…

x可表示为x=0.x1x2…xk…的形式。确定了规范小数表示之后，上述表述仍然是唯一的。

同理可证，任意实数都可表示为十进无穷小数。

3 应用

实数的十进小数表示公理，在实数理论中有广泛的应用。

例1证明全体实数集R不可数。

证明因实数集R与区间(0,1)对等，只需证明(0,1)不可数。

运用反证法。假设(0,1)中的全体实数可数，则(0,1)区间的全体实数可用一个序列表示出来，设(0,1)={x1,x2,…,xn,…}。由实数的十进小数表示公理，每一个数的规范小数可表示为:

x1=0.a11a12…a1k…

x2=0.a21a22…a2k…

⋮

xn=0.an1an2…ank…

…

取x=0·b1b2…bn…，其中:

则x≠xn(n=1,2,…)，即x与(0,1)区间的任意一个实数都不相等。但显然x∈(0,1)，故矛盾。因此(0,1)是不可数集，即全体实数集R不可数。

例2证明n维欧氏空间Rn与实数集R对等，即Rn～R。

证明要证Rn～R，只需证明R2～R，其余类似。

记集合D=(0,1)×(0,1)，因映射T:D→R2:

为一一映射，故R2～D。

同理，R～(0,1)。故只需证明D～(0,1)。

∀(x,y)∈D,由小数表示公理，x,y有唯一的正规表示：

x=0.a1a2…an…

y=0·b1b2…bn…

作映射f:D→(0,1):

(x,y)→zz=0.a1b1.a2b2…anbn…

显然，f为一一映射，故D～(0,1)。

综上，R2～R。