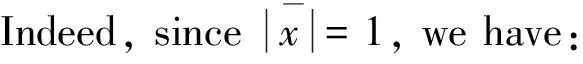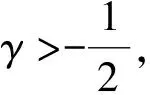A Dimension Free Inequality
[Abstract]To deduce regularity of p-harmonic mappings, the following important inequality plays a fundamental role given by Giaquinta-Modica and Acerbi-Fusco: For any γ>-12, there exist constants c1,c2>0 depending only on γ and n, such that for any x,y∈Rnand μ≥0, there holds: c2x-y≤(μ2+x2)γx-(μ2+y2)γy(μ2+x2+y2)γ≤c1x-yIn this paper this inequality is improved by showing that the above inequality holds in any Hilbert space with c1,c2 depending only on γ. This implies that the above inequality is dimension free.
[Keywords]Hilbert space; inequality; dimension free
1 Introduction and Main Result
Since the seminar work of Morrey[1], harmonic mappings become one of the central topics in geometric analysis, see e.g. Schoen-Uhlenbeck[2]and the monograph of SchoenYau[3], and the references therein. A natural generalization of harmonic mappings is the so calledp-harmonic mappings for 1 Motivated by the useful applications of the above inequality inp-harmonic mappings, and also under the consideration that it may have other potential applications, in this paper, we will further show that the above two constantsc1,c2depend only onγand are independent of the dimensionn. Moreover, we will prove that the above inequality holds in Hilbert spaces as well. In this way, we improve the result of Acerbi-Fusco [6, Lemma 2.2]. To state our result, denote byHan arbitrary Hilbert space with inner productand denote the norm ofHby |x|=x∈H. Our main result reads as follows. In the following, we will also usec1,c2to denote different constants that depend only onγfrom line to line. The proof of Theorem 1 is reduced to the following lemma. (1) ProofSuffices to assumeμ>0 and|x|≥|y|>0. The result is trivial wheny=0. Notice that: So it is equivalent to prove that, for anyμ>0 and|x|≥|y|>0, there holds: (2) for somec1,c2>0 depending only onγ. We divide the proof into two cases. Case1γ≥0. Thus: This yieldsc2(γ)=4-1-γin (2). Since: we have: Thus we can takec2(γ)=1 in (2).So it remains to prove the existence ofc1(γ)in (2). To this end, let: such that: (3) Sinceγ<0, we have: we claim that: This implies: The claim is proved. Now we claim that: Hence we can take: This proves the claim, and thus (3) follows. The proof is complete. Now we can prove Theorem 1. For simplicity, denote: ProofofTheorem1It is enough to prove the result forμ>0. The caseμ=0 follows by approximation. Then,μ>0 implies that the Hilbert space valued functionf=f(x)is smooth for anyγ>0. So: whereDf(x) is the Gateaux derivative off: for anyx,z∈H. Hence, for anyz∈H, we have: This implies: Combining Lemma 1 yields the results. We also obtain a useful inequality from Theorem 1. In particular, we have: ProofNote that the second inequality is a special case of the first one.By Theorem 1 we have: For another side, note that: ≥min{ 1,1+2γ ≥min{ 1,1+2γ wherec2(γ)is defined as in (1). The proof is complete.
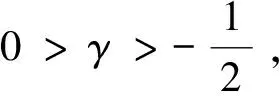

2 Proof of Main Result