基于盖尔圆定理的矩阵特征值估计
雍龙泉
(陕西理工大学 数学与计算机科学学院, 陕西 汉中 723000)
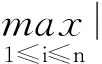
1931年,Gerschgorin提出了著名的盖尔圆定理,这便是矩阵特征值估计的开山之作。矩阵特征值估计是矩阵分析中的热点问题[5-11],在很多领域都起到重要的作用。本文利用盖尔圆定理,给出一般矩阵特征值在复平面上的大概范围。通过相似变换,使得所有盖尔圆相互孤立,从而每个孤立的盖尔圆内仅含有一个特征值;且在保证所有盖尔圆孤立的同时,尽可能使得“所有盖尔圆围成区域的面积和”减少,以便更精确地估计出矩阵特征值的范围。
1 盖尔圆定理
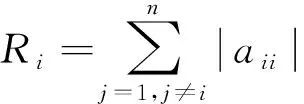
定理1(盖尔圆定理1[12]) 矩阵A=(aij)∈Cn×n的一切特征值都在它的n个盖尔圆的并集之内。
定理2(盖尔圆定理2[12]) 由矩阵A的所有盖尔圆组成的连通部分中任取一个,如果它是由k个盖尔圆构成的,则在这个连通部分中有且仅有A的k个特征值(盖尔圆相重时重复计数,特征值相同时也重复计数)。
例1 证明矩阵A能够相似于对角矩阵,且矩阵A的特征值都是实数。这里
分析这是一个n阶非对称方阵,文献[13-14]中指出该矩阵为广义正定矩阵。但是求其特征值或特征向量似乎难以用《线性代数》或者《高等代数》的知识进行计算[15-16]。
证明矩阵A的n个盖尔圆为
G1={z:|z-2|≤1},
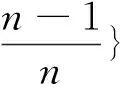
显然这n个盖尔圆是相互孤立的,所以矩阵A有n个互不相同的特征值,从而A相似于对角矩阵。又因为Gi(i=1,2,…,n)关于实轴对称,且每个盖尔圆中只有A的一个特征值,所以A的特征值都是实数(因为复特征值一定成对共轭出现[17])。
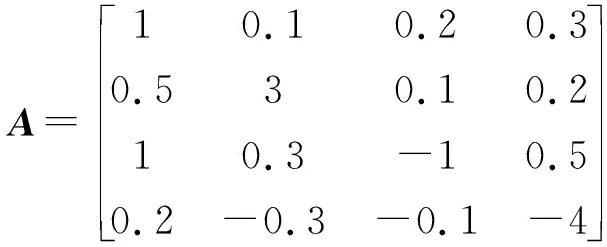
解矩阵A的4个盖尔圆为
G1={z:|z-1|≤0.6},
G2={z:|z-3|≤0.8},
G3={z:|z+1|≤1.8},
G4={z:|z+4|≤0.6}。
如图1,利用定理2可知A的4个特征值全落在4个盖尔圆并集内。鉴于G2和G4孤立,故G2和G4中各有一个特征值;而G1与G3构成的连通部分含有两个特征值。事实上,该矩阵的4个特征值为{-3.989 3,-1.111 8,1.075 7,3.025 3}。
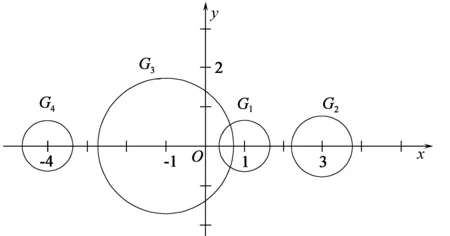
图1 例2对应的盖尔圆
2 特征值估计
鉴于相似变换不改变矩阵的特征值,因此借助相似变换来缩小盖尔圆的半径,将盖尔圆进行分离,使得每一个盖尔圆内恰好含有一个特征值,从而进一步明确特征值的范围。
取对角阵做相似变换:选取P=diag(p1,p2,…,pn),其中pi>0,i=1,2,…,n。则
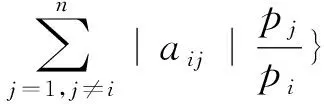

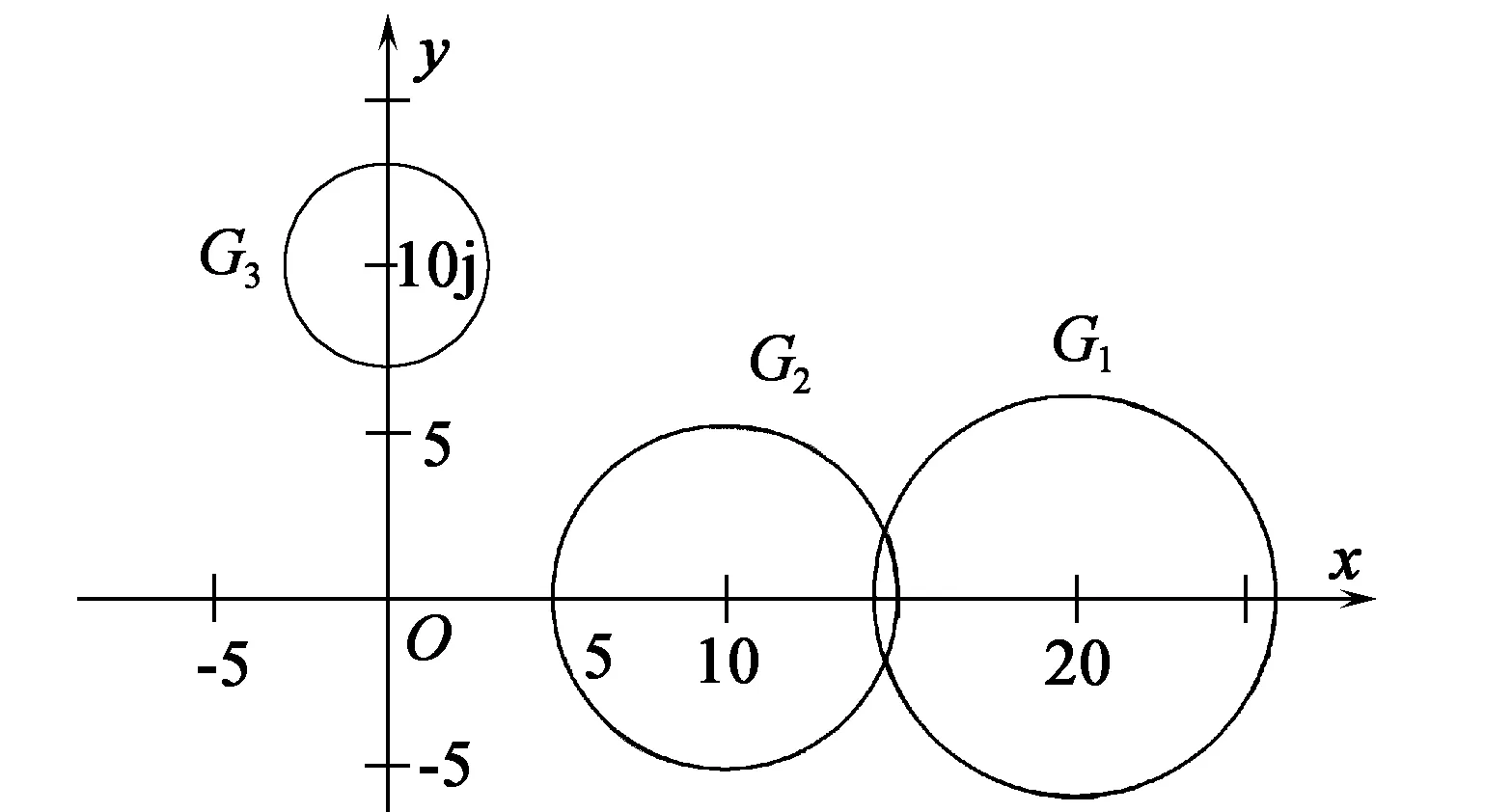
图2 例3对应的盖尔圆(a)
解矩阵A的3个盖尔圆为
G1={z:|z-20|≤5.8},
G2={z:|z-10|≤5},
G3={z:|z-10j|≤3}。
如图2所示,G1与G2构成的连通部分含有两个特征值;G3中有A的一个特征值。事实上,该矩阵的3个特征值为{-0.118 1+9.910 4j,8.341 3+0.058 1j,21.776 8+0.031 5j}。
图2中3个盖尔圆所围成区域的面积和S满足
π+25π+9π=67.64π。
下面设法缩小盖尔圆G1与G2的半径(或者说,适当增大盖尔圆G3的半径),使得G1与G2分离。
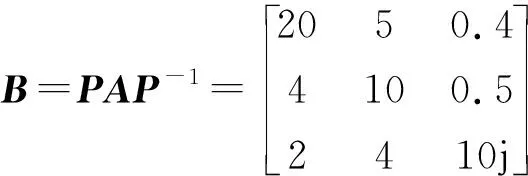
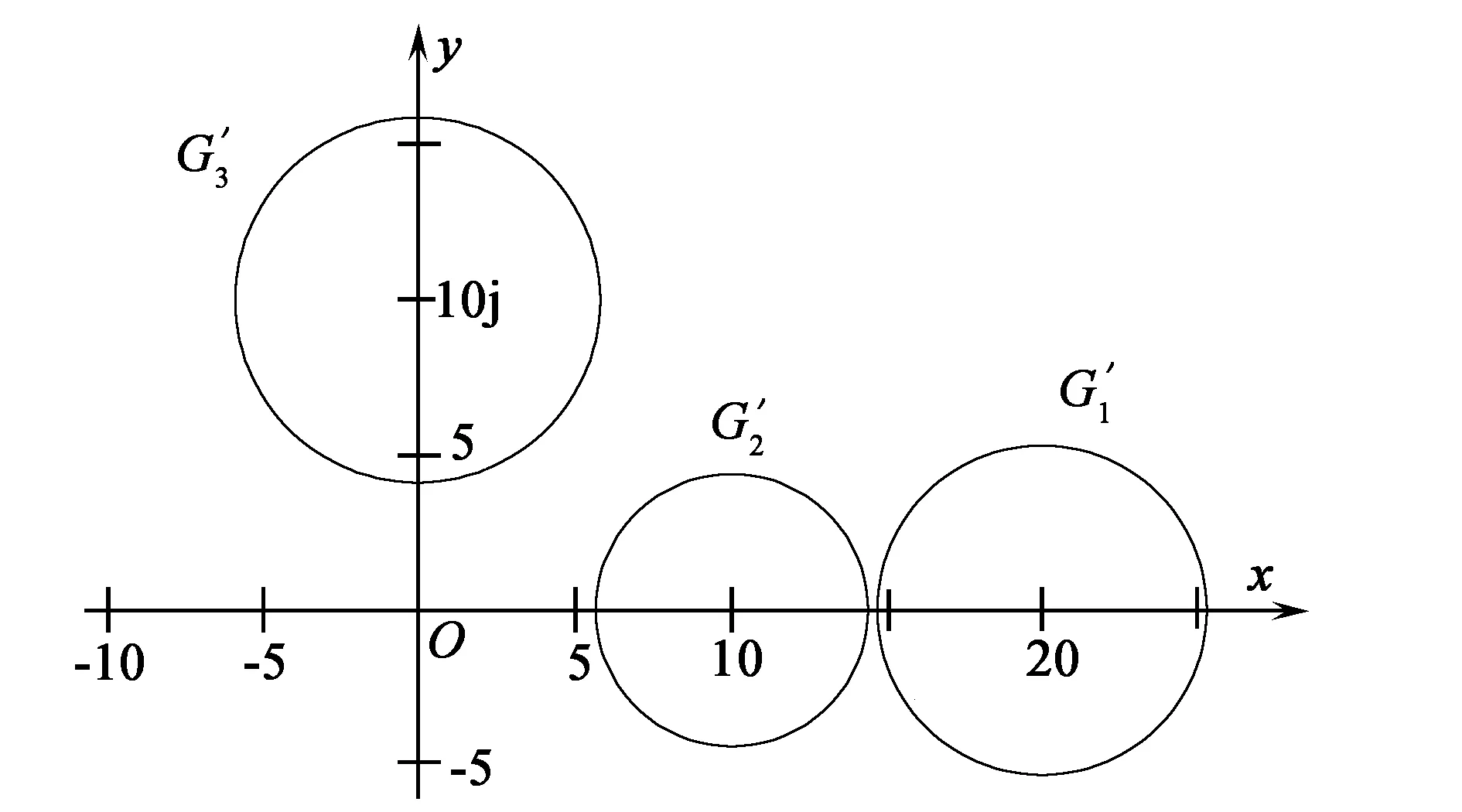
图3 例3对应的盖尔圆(b)
{z:|z-20|≤5.4},

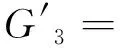

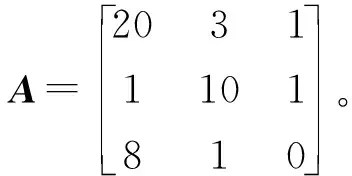
解A的3个盖尔圆为
G1={z:|z-20|≤4},
G2={z:|z-10|≤2},
G3={z:|z|≤9}。
如图4所示,G2与G3构成的连通部分含有两个特征值;G1中有A的一个特征值。事实上,该矩阵的3个特征值为{-0.376 1,9.597 6,20.778 5}。
图4中3个盖尔圆所围成区域的面积和S满足:97π=SG1+SG3 图4 例4对应的盖尔圆(a) {z:|z-20|≤5}, 图5 例4对应的盖尔圆(b) 说明:选取正数p1,p2,…,pn的一般原则:欲使A的第i个盖尔圆缩小,可取pi<1,其余取为1;反之,欲使A的第i个盖尔圆放大,可取pi>1,其余为1。通过相似变换后所有盖尔圆围成区域的面积和有可能增大(例3),也有可能减小(例4);若相似变换后所有盖尔圆的面积和小于变换前的面积和(例4),则表明矩阵特征值的范围更精确。 注:如何使相似变换后所有盖尔圆围成区域的面积和减少,暂无统一办法,需具体问题具体分析。 本文利用盖尔圆定理,通过相似变换,初步估计出了矩阵特征值的范围。所以本文开始提出的问题就可容易解决。设实对称n阶方阵A的任一特征值为λ,Gi为第i个盖尔圆,记A的所有盖尔圆的并集为G=∪Gi;由定理2知,λ∈G。因此总可以在G的外面取一个正数ε,使得A+εI为半正定矩阵。 例如在研究方微分方程数值解时,常需考虑如下三对角矩阵[18] 根据定理2,相应的盖尔圆为G1={z:|z+2|≤1}和G2={z:|z+2|≤2}。设λ为矩阵A的任一特征值,则λ∈(G1∪G2);由于矩阵A的特征值皆为实数,故λ∈[-4,0]。因此,只要选取ε≥4,此时A+εI就是半正定矩阵。该结论在矩阵扰动分析及优化理论[19-20]中具有重要的应用前景。

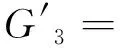

3 结束语


