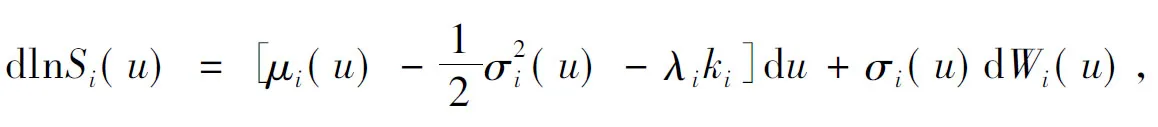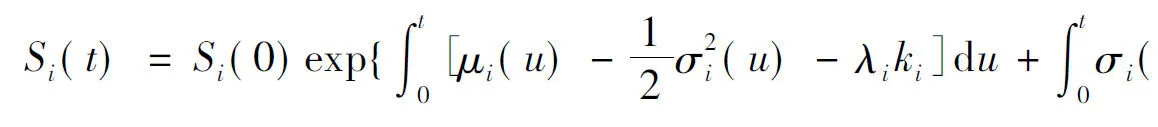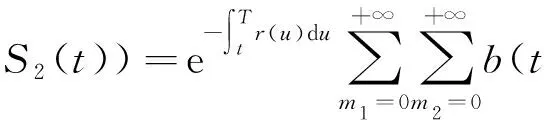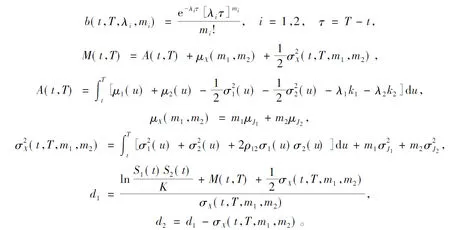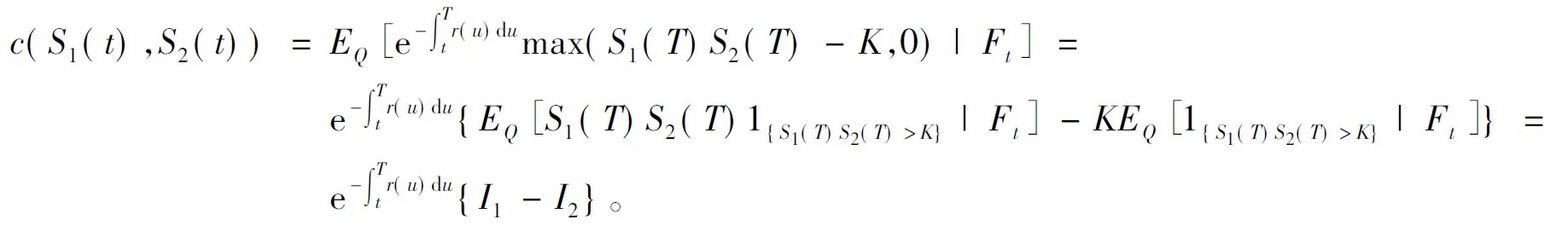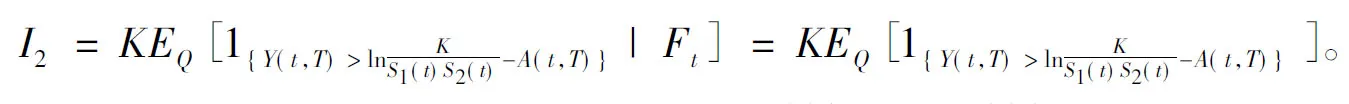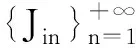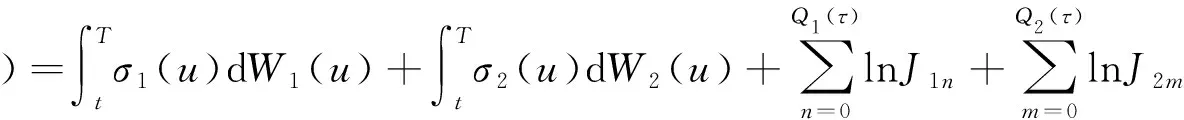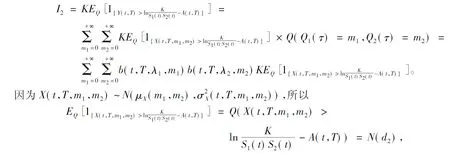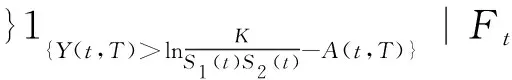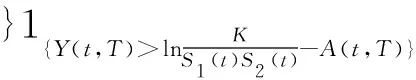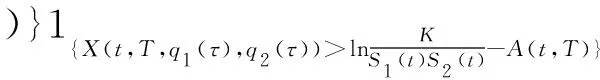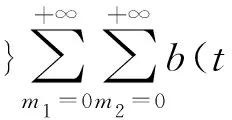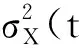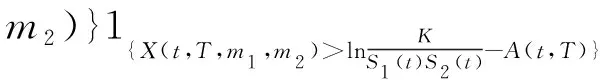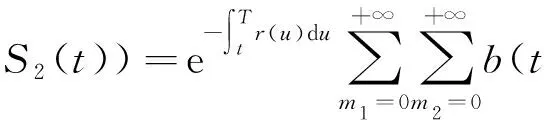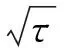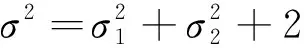跳扩散模型下乘积期权的定价

刘佳玥， 李翠香

(河北师范大学 数学与信息科学学院， 河北 石家庄 050024)

自20世纪70年代以来，金融衍生产品在全球范围内迅猛发展，期权的定价问题越来越引起国内外数学家及金融学家的重视。1900年，法国数学家Bachelier[1]首先提出了关于期权定价的问题。1973年，Black和Scholes[2]第一次提出了期权定价的Black-Scholes模型(以下简称B-S模型)，并进一步得出了欧式看涨和看跌期权的价格公式。但是，B-S模型中的一些假设并不能完全反映实际市场中的某些现象，为了使期权的定价模型更加贴合实际市场，许多学者对B-S模型进行了扩展，比如，将常数参数扩展为关于t的确定函数。2008年，刘海媛等[3]研究了参数与时间有关的几种新型期权的定价。近几年，跳扩散模型下的期权定价成为了研究热点。Merton[4]最早提出了期权定价的跳扩散模型。2012年，李翠香等[5]得到了基于随机利率下跳-扩散过程的复合期权定价。2017年，耿延静[6]研究了跳扩散模型下亚式期权的定价。袁国军等[7]、邓国和[8]、Ren Xue-min等[9]、Vipul Kumar Singh[10]也都得到了期权定价的重要结论。本文主要研究跳扩散模型下乘积期权的定价公式。

1 预备知识

乘积期权是以两个资产的价格或者股票指数的乘积作为标的物执行的期权。资产价值为S1(t),S2(t)，到期日为T，执行价格为K的看涨与看跌乘积期权在到期日的收益分别为

c(S1(T),S2(T))=max(S1(T)S2(T)-K,0),

p(S1(T),S2(T))=max(K-S1(T)S2(T),0)。

乘积期权有两个主要的应用，一个是外股本币期权，另一个是公司收入期权。2014年，Zhang P G[11]得到了普通欧式乘积期权的定价公式。

本文设(Ω,F,{Ft},Q)为带有域流{Ft}的概率测度空间，其中Ω为样本集合，F为Ω生成的σ域，Q为风险中性测度，{Ft}为本文所涉及到的随机过程所生成的域流。假设乘积期权的资产价格Si(t)服从如下随机微分方程(简称SDE)：

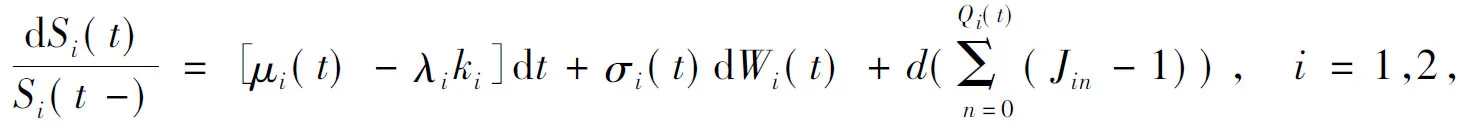
(1)

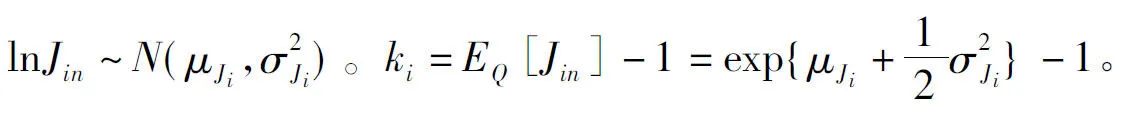
2 跳扩散模型下乘积期权的定价

首先介绍几个重要的引理。

引理1[12](Ito’s引理) 设Xi(t)(i=1,2,…,n)是具有如下随机微分形式的Ito’s过程:

dXi(t)=μi(t)dt+σi(t)dWi(t),i=1,2,…,n，

其中Wi(t)为布朗运动，若n元函数f(x1,x2,…,xn)具有二阶连续偏导数，则

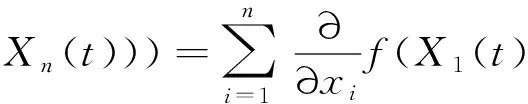
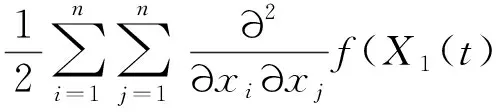
引理2 若随机变量X是测度Q下期望为μ、方差为σ2的正态分布变量，即X～N(μ,σ2)，则

(2)

其中N(·)表示标准正态分布的累积函数。

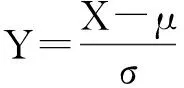
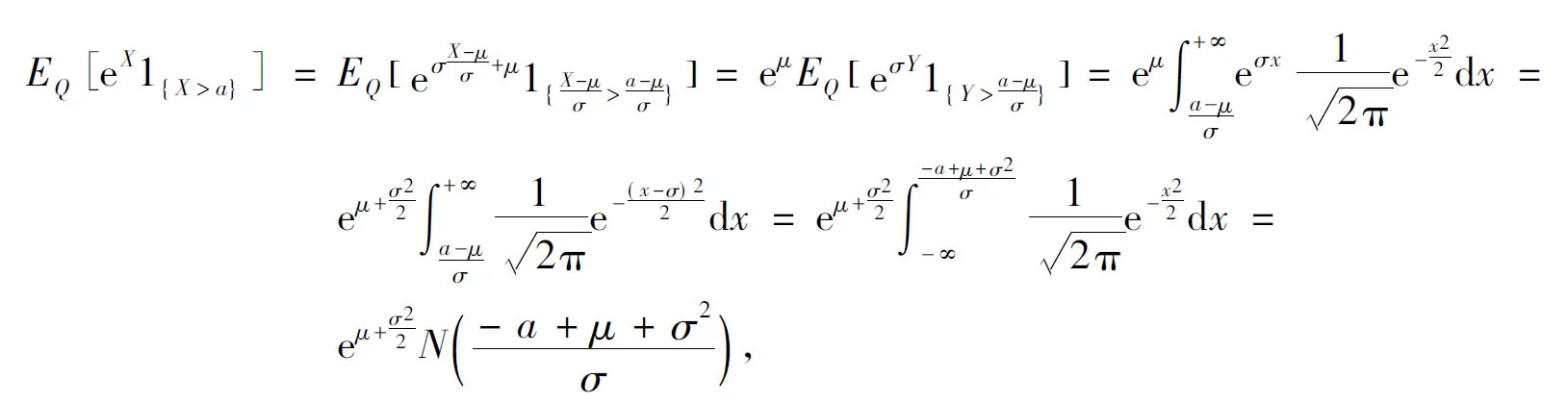
由此引理2得证。

引理3 假设资产价格Si(t)(i=1,2)服从SDE(1)，则

(3)

其中当Qi(T)

证明当Si(u)在[0,t]内没有发生跳跃时，则由引理1可知：当u∈(0,t)时，

两边从0到t积分得

假设只在T1∈[0,t]时刻发生了一次跳跃，则

因此

当跳跃次数为Qi(t)时，则

从而有

由此引理3得证。

定理1 设乘积期权的两资产S1(t),S2(t)服从SDE(1)，则到期日为T，执行价格为K的看涨乘积期权在t时刻的价格为

[S1(t)S2(t)exp{M(t,T)}N(d1)-KN(d2)],

其中利率r(u)为关于时间u的确定函数，u∈[t,T]，

证明由风险中性定价原理可得

(4)

首先计算I2，令

则由引理3得

S1(T)S2(T)=S1(t)S2(t)exp{A(t,T)+Y(t,T)}。

(5)

由布朗运动及Possion过程的独立增量性可知

得

由此得

,T,λ1,m1)b(t,T,λ2,m2)KN(d2)。

(6)

下面计算I1。由式(5)及布朗运动和Possion过程的独立增量性可知

由此得

,T,λ1,m1)b(t,T,λ2,m2)S1(t)S2(t)exp{M(t,T)}N(d1)。

(7)

结合式(4)、(6)和(7)定理1得证。

定理2 设乘积期权的两资产S1(t),S2(t)服从SDE(1)，则到期日为T，执行价格为K的看跌乘积期权在t时刻的价格为

[KN(-d2)-S1(t)S2(t)exp{M(t,T)}N(-d1)],

参数记号同定理1。

推论1 在SDE(1)中，当μi(t)=μi,σi(t)=σi均为常数，λi=0时，乘积期权在t时刻的价格为

c0(S1(t),S2(t))=e-rτ[S1(t)S2(t)eμτN(d10)-KN(d20)],

p0(S1(t),S2(t))=e-rτ[KN(-d20)-S1(t)S2(t)eμτN(-d10)],

其中

证明把μi(t)=μi,σi(t)=σi,λi=0代入定理1和定理2可得推论1。

注推论1正是文献[11]中的结果。

本文假设资产价格服从带跳的几何布朗运动，利用Ito’s积分的性质得到乘积期权的定价公式。因为这个模型更符合现实市场的实际情况，所以研究更具有实际意义。