基于因子分析的物质浓度与颜色读数关系的探究

,

(1.安徽城市管理职业学院公共教学部，安徽 合肥 230011；2.合肥师范学院数学与统计学院，安徽 合肥 230601)

0 引 言

比色法是化学邻域中一种常见的测量物质浓度的方法。该方法指的是把物质溶液经过一定的处理后，产生相应的颜色，再把该颜色与一个标准比色阶进行对比，就可以确定待测物质的浓度档位了。比色法作为一种定量分析的方法，大约开始于19世纪的30～40年代。目视比色法就是其中一种，但由于眼睛观察存在误差，现如今拍照即可得到清楚的颜色分辨率，因此希望借助现代化拍照技术，建立颜色读数和物质浓度的数量关系，即只要输入照片中的颜色读数就能够获得待测物质的浓度，基于实验数据的基础上来探究这两者之间的关系。

1 问题的提出

以硫酸铝钾为例，给出该物质的在不同浓度下的一组颜色读数的平均值(每种浓度做了不止一次实验)(如表1所示)，即B、G、R、H、S的颜色读数。这里，B、G、R是将颜色利用RGB色彩模式，分解为蓝(B) 、 绿(G)、红(R)三个颜色通道的值.以及颜色参数，色调(H)，饱和度(S)。

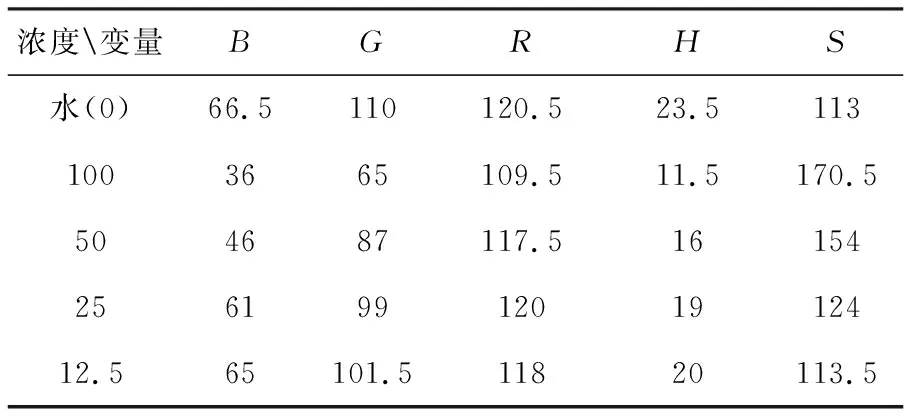
表1

现探究由这组数据能否确定颜色读数和物质浓度之间的关系。

2 因子分析法

因子分析旨在利用少数几个变量来表示原来多个变量的主要信息，是常用的数据降维方法之一。以表1数据为例，称B、G、R、H、S为原始变量，它们与潜在因子的关系用如下模型来刻画：

(1)

其中，l1…lm是潜在因子，是B、G、R、H、S都包含的因子，称作共性因子.m是潜在因子个数，这里1m5， 通过此因子分析模型来确定m=1还是m>1。e1…e5为5个只包含在某个原始变量中，只对一个原始变量起作用的个性因子，是该变量特有的特殊因子。cij为第j个潜在因子在第i个原始变量中的因子负荷.cij的绝对值越大，表示第j个潜在因子和第i个原始变量的关系越强。

利用SPSS软件来求解上述因子分析模型，求解过程中需经历如下几个重要步骤：

(1)因子提取。 通过分析原始变量之间的关系，从中提取出数量较少的因子。其中最常见的是主成分分析法和主轴因子法，此处选择主成分分析法。

(2)因子旋转。利用因子提取方法得到的结果虽然保证了因子之间的正交性，但因子对变量的解释能力较弱，不容易解释和命名。这时，可以通过因子模型的旋转变换，使得公共因子的复合和数接近1或者0，通过这种方法得到的公共因子对变量的命名和解释将变得更容易。在此问求解过程中，若公共因子个数超过了1个，则做因子旋转。

(3)计算因子得分。计算因子得分的方法主要有回归分析法、巴特利特法和Anderson-Rubin法.这里利用线性回归法计算因子得分.

3 问题的求解与分析

3.1 数据处理

将表1中的数据录入SPSS软件，并利用因子分析法(1)计算，得到表2如下。

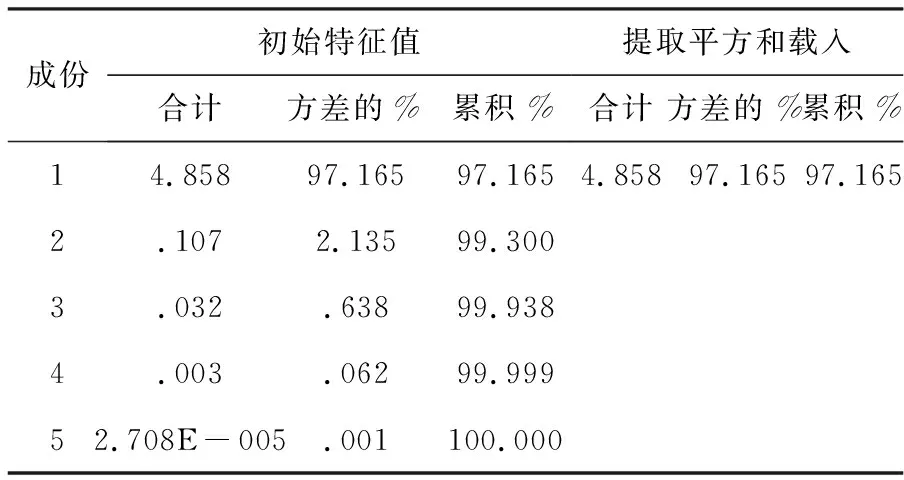
表2

此表中，第1列是因子分析的5个初始解的序号；第2列是因子变量的方差贡献，是衡量因子重要程度的指标；第3列是各个因子变量的方差贡献率；第4列是因子变量的累积方差贡献率；第5--7列是从初始解中按照方差贡献率提取公共因子后对原变量总体的描述情况。

3.2 结果分析

从表2的第5--7列可以看出，按照方差贡献率提取的公共因子只有1个。从第3列可以看出，该公共因子的方差贡献率达到97.165%，其余初始解的方差贡献率都很小，加起来不超过5%。这说明，该公共因子对B、G、R、H、S的解释能力非常强。由于实验过程中只改变浓度，其他条件不变，因此，该公共因子就是浓度。或者说，浓度的变化唯一决定着组胺颜色读数的变化，且决定程度达到97.165%。

3.3 实验数据优劣评价

由于实验数据可能由于观察、记录等原因造成误差，可以通过表2对于实验数据优劣进行评价。可考虑两方面：一是看公共因子的个数，公共因子只有1个的数据强于拥有2个公共因子的数据。在公共因子个数相同的情况下，再看第一公共因子的方差贡献率，方差贡献率高的数据强于方差贡献率低的数据。根据以上所述，由表2中看出硫酸铝钾的实验数据即表1还是比较好的。

4 问题的检验与误差分析

4.1 单因素方差分析

单因素方差分析是指对单因素试验结果进行分析，检验因素对试验结果有无显著性影响的方法。

因素：影响研究对象的某一指标、变量。本文所指为物质的浓度。

水平：因素变化所分的组别。文中的例子指浓度不同分为不同的组，即不同的水平。如硫酸铝钾实验数据有六个不同的浓度(0、0.5、1、1.5、2、5ppm)，可分为六组，序列号标位1、2、3、4、5、6。

单因素方差分析模型，主要含有以下比较重要的计算步骤：

(1)建立检验假设，确定检验水准

H0(零假设)：m组样本的均值都相同，即μ1=μ2=...=μm。例中m=6，假设6组浓度下的颜色读数均值相同。

H1：m组样本的均值不相同或不全相同，即各μi不等或不全相等。

取显著性水平α=0.05。

(2)计算组间、组内差异，确定P值(显著性)作出统计性判断

一般认为不同的组别均值间差别源于两个：组间差异(实验条件的变化)指的是不同的处理形成的不同组间的差异；组内差异(随机误差)指的是同一组间某种原因形成的差异，如测量误差等。例中组间差异为不同浓度之间的差异。将组间、组内差异除以各自的自由度，得到其均方.如果组间均方远远大于组内均方，即各组间具有显著性差异。例中所指为不同浓度间的读数均值差异远远大于同一浓度下读数均值差异。从而可推断物质浓度和颜色读数具有显著性相关。

同时，当P<0.05拒绝零假设，组别间有差异，具有统计意义，可进一步深入分析；否则P>0.05不能拒绝零假设，不用进行多重比较。

4.2 方差齐性检验

针对硫酸铝钾指标B不同浓度的颜色数据(表3)进行分析。

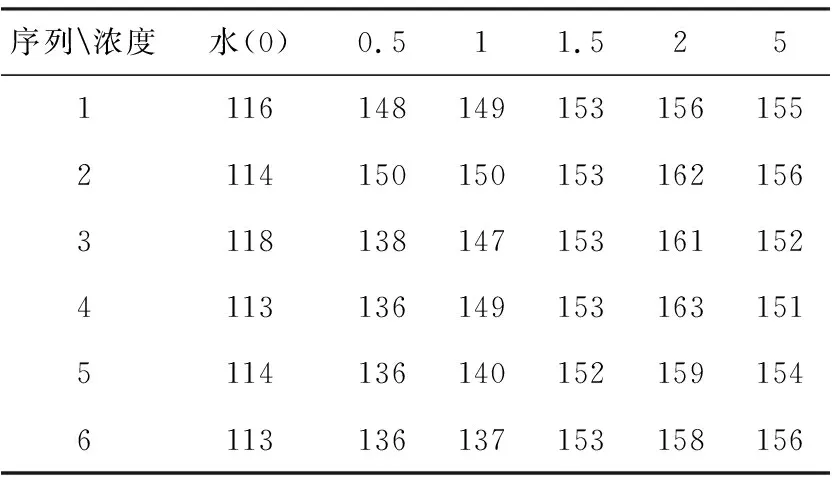
表3

进行方差分析前，首先进行方差齐性检验。检验不同浓度下观察得各颜色读数总体方差是否相等。将表3对应的数据录入SPSS软件，得到如下表格4。

表4

该表中第2、3列是自由度，第4列是P值.可见显著性P值均小于0.05，说明不同浓度下，硫酸铝钾B指标的方差是不等的，也即不同浓度对B指标是有影响的。

4.3 单因素方差分析

同样利用SPSS软件可得如下表5。

表5

该表的第2列看出，组间离差平方和为7836.941，组内离差平方和为445.762，总的离差平方和为8282.703，第4列组间均方为1567.388远远大于组内均方14.379。反映出不同浓度对硫酸铝钾B指标颜色读数具有显著性影响。同时从最后一列显著性P值均小于0.05看，各组之间均有很明显差别，验证了颜色读数受浓度影响大。

由此，通过单因素方差分析，可得出结论物质浓度与颜色读数具有显著性相关。但以上分析仅为硫酸铝钾指标B的分析结果，对于其余四项指标G、R、H、S完全可使用同样的模型并利用SPSS软件进行验证。

5 结 语

综上所述，基于实验中所给出的数据，首先利用因子分析的方法进行求解并得出结论，然后利用单因素方差分析验证了因子分析结果的正确性。即物质浓度对颜色读数具有显著影响。为比色法的研究进一步提供了理论基础。