简单线性规划问题的常见类型和解法
江苏省启东市折桂中学(226200) 胡周华
简单线性规划是高中数学教学必修内容之一,基本思想是在一定的约束条件下,通过数形结合求函数的最值,线性规划问题已成为近几年高考的热点问题.
考试大纲中要求:了解二元一次不等式的几何意义,能用平面区域表示二元一次不等式组,能从实际情境中抽象出一些简单的二元线性规划问题,并加以解决.等级要求A级.
类型一 二元一次不等式(组)所表示的平面区域的有关问题
1 判断二元一次不等式Ax+By+C≥0表示的平面区域是在直线的哪一侧的方法:
(1)特殊点检验法
②当C=0时,取不在直线上的点(x0,0)或(0,y0)使不等式成立时就含此点的平面区域;不成立时,就是其另一侧区域.
(2)标准式快速判断法.
将二元一次不等式Ax+By+C≥0化为y≥kx+b或y≤kx+b和x≥b或x≤b.
①y≥kx+b表示的平面区域在直线y=kx+b的上方;
②y≤kx+b表示的平面区域在直线y=kx+b的下方;
③x≥b表示的平面区域在直线x=b的右方;
④x≤b表示的平面区域在直线x=b的左方.
例1画出二元一次不等式(组)所表示的平面区域.
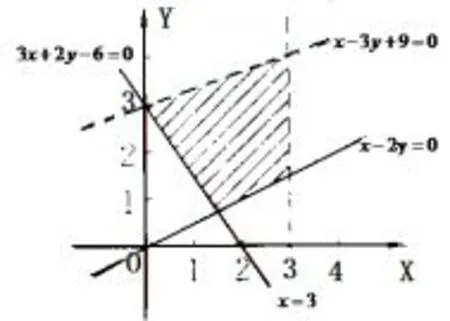
图1
解不等式x<3表示直线x=3左方的平面区域,不等式2y≥x表示直线x-2y=0及其左上方的平面区域,不等式3x+2y≥6表示直线3x+2y-6=0及其右上方的平面区域,不等式3y<x+9表示直线x-3y+9=0右下方的平面区域.综上,可得不等式所表示的平面区域如图1阴影部分所示.
例2(2016年高考浙江卷理科)在平面上,过点P作直线l的垂线所得的垂足称为点P在直线l上的投影.由区域中的点在直线x+y-2=0上的投影构成的线段记为AB,则|AB|=()
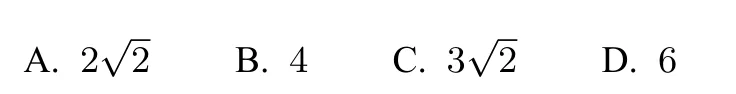

图2
解如图2,△PQR是可行域,区域内的点在直线x+y-2=0上的投影构成了线段R′Q′,即AB,而R′Q′=RQ,由得Q(-1,1),由得R(2,-2),|AB|=|QR|=.故选C.
点评本题考查线性规划.先根据不等式组画出可行域,再根据题目中的定义确定|AB|的值.画不等式组所表示的平面区域时要注意通过特殊点验证,防止出现错误.
2 求二元一次不等式组所表示平面区域的面积
先要画出不等式组表示的平面区域,然后根据区域的形状求面积.利用图形的形状,直观地分析图形的结构特征,挖掘其隐含条件,寻找解题的捷径.
例3求不等式组所表示的平面区域的面积.
解可行域为图3中阴影部分及其边界.由图形知BC=10,△ABC的边BC上的高为5,所以S△ABC=.
图3
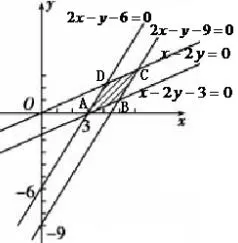
图4
例4(2013年高考北京卷文科)已知点A(1,-1),B(3,0),C(2,1).若平面区域D由所有满足的点P组成,则D的面积为___.
解,设P(x,y),由,得
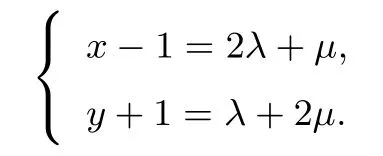
点评本题考查了平面向量的坐标运算、线性规划等知识;同时又考查了转化及数形结合思想,综合能力要求较高,体现近几年来,线性规划问题的考查逐渐从简单向综合型方向转变的趋势.
3 求二元一次不等式组所表示的平面区域内的整数解
求区域内正整数解的方法如下:先要画出不等式组表示的平面区域,然后根据区域的范围,简单的问题可直观分析,确定区域内的整数解;复杂的问题可列表统计,再确定满足条件的整数解.的整点的个数.
例5在直角坐标系中,求满足不等式组
解不等式组所表示的平面区域为图5中阴影部分及其边界.即△OAB,其中A(6,2),B(2,6).所以x∈[0,6],y∈[0,6].目标函数P(x,y),其中x,y∈N,满足条件的整点列表如下:
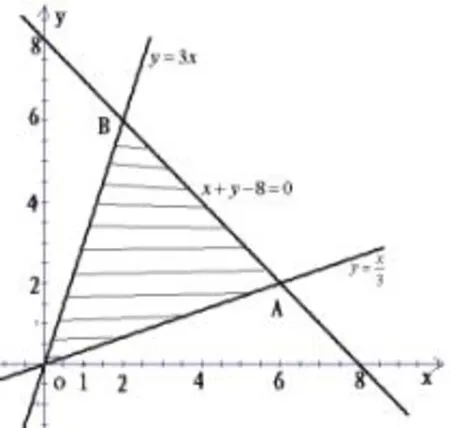
图5

所以所求整点的个数为21.
类型二 利用线性规划求目标函数的最值问题
1 利用图解法解线性规划问题的一般步骤:
(1)写出可行解的不等式组,画出可行域;
(2)建立目标函数,作出目标函数的等值线;
(3)在可行域内平移目标函数等值线,确定最优解.简称一画、二移、三求.
例6(2017高考北京文数第4题)若x,y满足则x+2y的最大值为()
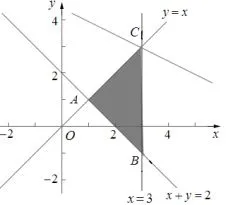
图6
A.1 B.3 C.5 D.9z=x+2y表示斜率为的一组平行线,当z=x+2y过点C(3,3)时,目标函数取得最大值zmax=3+2×3=9,故选D.
解如图6,画出可行域,
点评本题主要考查简单的线性规划.解决此类问题的关键是正确画出不等式组表示的可行域,将目标函数赋予几何意义.若可行域为封闭区域(即几条直线围成的区域),则区域端点的值是目标函数可能的最大值点或最小值点,求出直线交点坐标代入目标函数,通过比较可求出最值.
2 常见目标函数最值问题的求法
(1)求线性目标函数z=ax+by的最值,可转化为直线的斜截式:,通过一族平行直线与可行域有交点时,直线在y轴上截距的最值问题间接求出z的最值.(2)求目标函数的最值,可转化为求可行域内一点(x,y)与点(-a,-b)连线斜率的最值.
(3)求目标函数z=(x+c)2+(y+d)2的最值,可转化为求可行域内一点(x,y)与点(-c,-d)的距离的平方的最值.
例7(2016年高考江苏卷)已知实数x,y满足则x2+y2的取值范围是___.
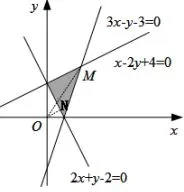
图7
解画出不等式组表示的平面区域(如图7),要求x2+y2的取值范围,即求阴影区域内的点到坐标原点O距离的平方,如图7所示,过O作垂线垂直于2x+y-2,此时垂足N到原点O的距离最短,即阴影区域内的点到坐标原点O的距离的平方最小,为;连接OM,如图7所示,M(2,3)点到坐标原点O的距离最长,所以到坐标原点O的距离的平方最大,为22+32=13.所以x2+y2的取值范围是.故答案为
点评本题主要考查线性规划.线性规划问题,首先明确可行域对应的是封闭区域还是开放区域、分界线是实线还是虚线(一般不涉及虚线),其次确定目标函数的几何意义,是求直线的截距、两点间距离的平方、直线的斜率、还是点到直线的距离等,最后结合图形确定目标函数最值或值域范围.
类型三 含有字母的线性规划问题
这类问题往往是在线性约束条件中或在目标函数中含有待定的字母,一定要正确地作出平面区域图形,依据图形作出合理的分析与推理,对字母进行必要的分类讨论,分类解决.
例8若不等式组表示的平面区域是一个三角形及其内部,求a的取值范围.

图8
解作出前三个不等式表示的平面区域如图8阴影部分所示,即可行域是△OAB内部及边界.其中.直线l:x+y=0过O,1过过B,当直线x+y=a在l1,l2之间或l3右上方时,满足题意,当x+y=a位于l2,l3之间时,区域为四边形,因此0<a≤1或.
点评本例0<a≤1容易得出,但极易忽视的情况,这是思维的片面性引发的错误.
例9(2013年高考浙江卷理科)设z=kx+y,其中实数x,y满足若z的最大值为12,则实数k=___.
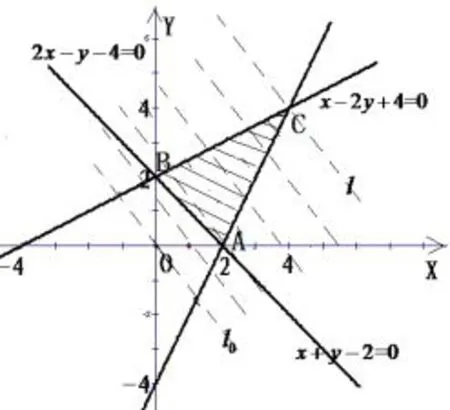
图9
解不等式组表示的平面区域如图9阴影部分所示,即△ABC内部及边界.其中A(2,0),B(0,2),C(4,4).由z=kx+y,得z是直线l:y=-kx+z在y轴上的截距.作l0:kx+y=0,把l0向右上方平移,(1)当时,l过点B(0,2),z有最大值,不满足条件.(2)当时,l过点C(4,4),z有最大值zmax=k×4+4=4k+4,由4k+4=12,得k=2.综上所述k=2.所以答案为2.
类型四 有关线性规划的实际应用问题
例10(2012年江西理)某农户计划种植黄瓜和韭菜,种植面积不超过50亩,投入资金不超过54万元,假设种植黄瓜和韭菜的产量、成本和售价如下表
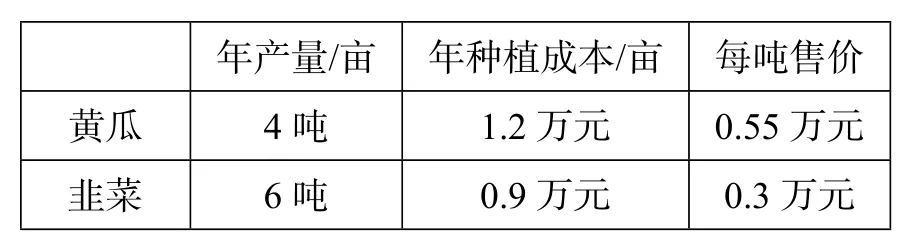
__________年产量/亩 年种植成本/亩__每吨售价___黄瓜4吨________1.2万元_____0.55万元_____________韭菜6吨_______0.9万元_____0.3万元_
为使一年的种植总利润(总利润=总销售收入-总种植成本)最大,那么黄瓜和韭菜的种植面积(单位:亩)分别为()
A.50,0 B.30,20 C.20,30 D.0,50
分析本题考查线性规划知识在实际问题中的应用,同时考查了数学建模的思想方法以及实践能力.
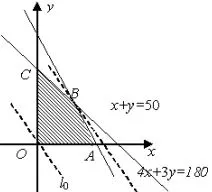
图10
解设黄瓜和韭菜的种植面积分别为x,y亩,总利润为z万元,则目标函数为z=(0.55×4x-1.2x)+(0.3×6y-0.9y)=x+0.9y.线性约束条件为即作出不等式组表示的可行域如图10阴影部分所示,其中A(45,0),B(30,20),C(0,50).平移直线z=x+0.9y,可知当直线z=x+0.9y经过点B(30,20),即x=30,y=20时,z取得最大值,且zmax=48(万元),故选B.
点评解答线性规划应用题的一般步骤可归纳为:
(1)审题—仔细阅读,明确有哪些限制条件,目标函数是什么?
(2)转化—设元,写出约束条件和目标函数,从而将实际问题转化为数学上的线性规划问题.
(3)求解—解这个纯数学的线性规划问题.关键是明确目标函数所表示的直线与可行域边界直线斜率间的关系;
求解过程:
①作图:画出约束条件所确定的平面区域和目标函数所表示的平面直线系中的任意一条直线l.
②平移:将l平行移动,以确定最优解所对应的点的位置.
③求值:解有关方程组求出最优解的坐标,再代入目标函数,求出目标函数的最值.
(4)作答—就应用题提出的问题作出回答.
类型五 线性规划综合问题
有些问题从表面看不是线性规划问题,但通过适当转化使之成为线性规划问题.
例11(2012年高考江苏卷)已知正数a,b,c满足:5c-3a≤b≤4c-a,clnb≥a+clnc,则的取值范围是___.
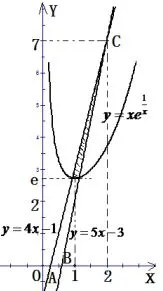
图11
解

所以题目转化为:已知x,y满足求y的取值范围.
作出(x,y)所在平面区域(如图11的阴影部分所示),易知C(2,7),直线y=4x-1、y=5x-3分别与x轴交于A,B,其中,所以.令,由,得x=1,所以y在上递减,在[1,2]上递增,所以.将(1,e)代入(1)成立,所以y≥e.所以e≤y≤7,即的取值范围是[e,7].
例12(2015高考浙江卷)若实数x,y满足x2+y2≤1,则|2x+y-2|+|6-x-3y|的最小值是___.

图12
解x2+y2≤1表示圆x2+y2=1及其内部,易得直线6-x-3y=0与圆相离,故|6-x-3y|=6-x-3y,当2x+y-2≥0时,|2x+y-2|+|6-x-3y|=x-2y+4,如图12所示,可行域为小的弓形内部,目标函数z=x-2y+4,则可知当时,z=3;min当2x+y-2<0时,|2x+y-2|+|6-x-3y|=8-3x-4y,可行域为大的弓形内部,目标函数z=8-3x-4y,同理可知当时,z=3.综上所述,|2x+y-2|+|6-x-3y|min的最小值是3.
例13实系数一元二次方程x2+ax+2b=0有两个实根,一个根在区间(0,1)内,另一个根在区间(1,2)内,求的取值范围.
分析可将看作点(a,b)和(1,2)连线的斜率,利用数形结合可顺利使问题得到解决.
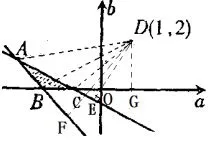
图13
解方程x2+ax+2b=0的两根在区间(0,1)和(1,2)内的几何意义是函数的图象与x轴的两个交点分别在区间(0,1)和(1,2)内,因此可得不等式组即在直角坐标系内,作出不等式组表示的平面区域(如图13),并解出点A(-3,1),B(-2,0),C(-1,0).而的几何意义是点P(a,b)和点D(1,2)连线的斜率.因为,如图13,,所以.

