对2018年高考导数大题的分析

浙江省杭州第二中学钱江校区(310053) 董泉发

2018年高考已经结束,笔者浏览了今年的8套试卷(不含文科),发现导数还是重头戏.今年除了北京和上海还是一以贯之地以数列压轴外,其他6份试卷全以导数压轴.北京卷导数题作为倒数第3题出现,上海卷没有考导数大题.纵观今年的导数大题,基本上都是考零点问题和极值点问题,实际上,极值点问题本质上还是零点问题,因为极值点是导函数的零点.零点问题和最值问题是高中代数(尤其是函数)的核心,因此高中代数(函数)部分复习重点应放在这两个问题上.今年的浙江卷和全国I卷都考了极值点偏移,其中浙江卷考的是类极值点偏移问题和函数零点与方程根的问题,北京卷和全国III卷都不约而同地考了极值问题,其背景涉及到极值的充分条件,这在高中数学中不讲,在大学数学分析中提到.全国II卷考的是零点问题,江苏卷和天津卷都考了函数零点和方程根的问题,江苏卷压轴题是数列和导数综合,考的是恒成立问题.

下面笔者对今年7套试卷中的导数大题逐一分析,不当之处,望同行批评指正.

题目1(2018年高考全国卷I理科数学第21题)已知函数

(1)略;(2)若f(x)存在两个极值点x1,x2,证明：.

思路简析(2)f(x)的定义域为.易知当a≤2时,f(x)单调递减,故f(x)存在两个极值点当且仅当a＞2.由于f(x)的两个极值点x1,x2满足x2-ax+1=0,所以x1x2=1,不妨设0＜.由于,所以等价于.构造函数,易知g(x)在(1,+∞)单调递减,又g(1)=0,从而当x∈(1,+∞)时,g(x)＜0.

题目2(2018年高考浙江卷第22题)已知函数.

(I)若f(x)在处导数相等,证明：f(x1)+f(x2)＞8-8ln2;

(II)若a≤ 3-4ln2,证明：对于任意k＞0,直线y=kx+a与曲线y=f(x)有唯一公共点.

思路简析

第(I)问方法1由得由基本不等式得因为,所以x1x2＞256.由题意得f(x1)+f(x2)=.构造函数在(256,+∞)上单调递增,故g(x1x2)＞g(256)=8-8ln2,即f(x1)+f(x2)＞8-8ln2.

第 (I)问方法 2令,则x1,x2是方程的两个不同的正根,也即是方程2tx2-x+2=0的两个不同的正根,

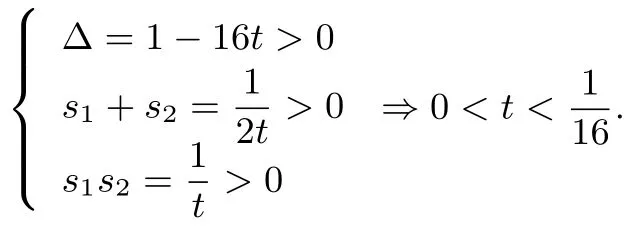
则

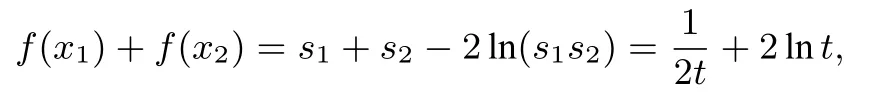
(II)对于任意的a∈R及k∈(0,+∞),先根据零点定理说明函数f(x)-(kx+a)有零点,再由得,证明当a≤3-4ln2时,h(x)在(0,+∞)单调递减即可.

评析全国I卷第2小问和浙江卷第I小问,考的都是极值点偏移和类极值点偏移问题,通常这种问题的处理都是整体考虑两个极值点(类极值点)：可以将其中一个极值点用另一个极值点表示或者二者都用第三个变量表示,转化为单一变量问题,通过构造函数解决问题.这样处理,原因在于两个极值点(类极值点)并不是相互独立的变量,而是彼此互相约束的.浙江卷导数第二问考的是函数零点与方程根的问题,其设问方式与天津卷导数题第三问类似.

题目3(2018年高考北京卷理科第18题)设函数f(x)=[ax2-(4a+1)x+4a+3]ex.

(I)略;(II)若f(x)在x=2处取得极小值,求点a的取值范围.

思路简析

第(II)问方法1注意到

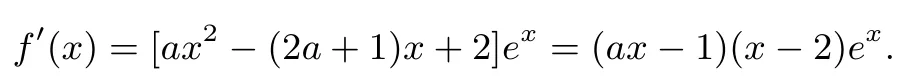
费马定理告诉我们,若函数f在x0可导,且x0为f的极值点,则f′(x0)=0.这就是说可导函数在点x0取极值的必要条件是f′(x0)=0.

若f是二阶可导函数,则有如下判别极值定理.

极值的第二充分条件：设f在点x0的某邻域U(x0,δ)内一阶可导,在x=x0处二阶可导,且.

(1)若f′(x0)＜0,则f在x0取得极大值;

(2)若f′(x0)＞0,则f在x0取得极小值.

对于应用二阶导数无法判别的问题,可借助更高阶的导数来判别.

极值的第三充分条件：设f在点x0的某邻域内存在直到n-1阶导函数,在x=x0处n阶可导,且,则

(1)当n为偶数时,f在x0取得极值,且当时取极大值,时取极小值.

(2)当n为奇数时,f在x0处不取极值.

第(II)问方法2,注意到,若f(x)在x=2处取得极小值,则必有,从而得到.

题目4(2018年高考全国III卷理科第21题)已知函数f(x)=(2+x+ax2)ln(1+x)-2x.

(1)若a=0,证明：当-1＜x＜0时,f(x)＜0;当x＞0时,f(x)＞0;

(2)若x=0是f(x)的极大值点,求a.

思路简析(1)略;

第(2)问方法1先证明若a≥0,由(1)知,当x＞0时,f(x)≥ (2+x)ln(1+x)-2x＞0=f(0),这与x=0是f(x)的极大值点矛盾.若a＜0,设函数

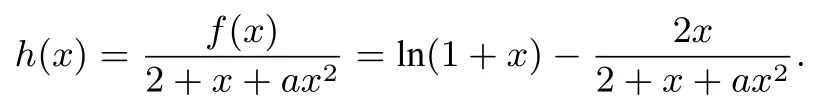
注这里为什么要除以2+x+ax2?原因在于lnx这种超越函数必须单独放在一边,也就是说lnx不能和其他函数结合在一起,必须分开,否则只求一阶导“求不净”(不能化到多项式函数),必须还得求二阶导,才能找到极值点.这是一种很聪明的做法.

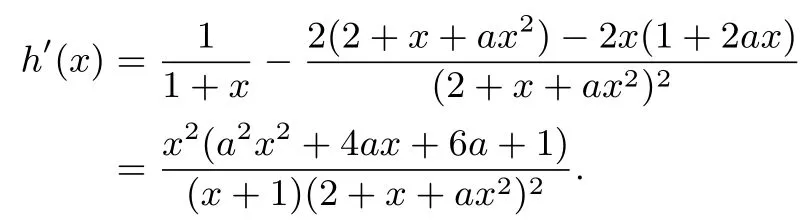
若6a+1＞0,当且时,h′(x)＞0,故x=0不是h(x)的极大值点;若6a+1＜0,则a2x2+4ax+6a+1=0存在根x1＜0,故当x∈(x1,0)且时,h′(x)＜0,所以x=0不是h(x)的极大值点;当 6a+1=0,则.则当x∈(-1,0)时,h′(x)＞0;当x∈(0,1)时,h′(x)＜0.所以x=0是h(x)的极大值点,从而x=0是f(x)的极大值点.综上,.

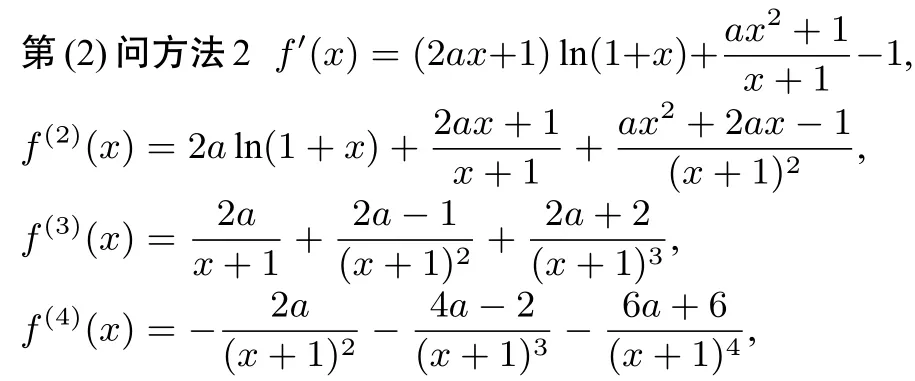
注意到f′(0)=f′′(0)=0,f(3)(0)=6a+1,根据极值第三充分条件可知,若x=0是f(x)的极大值点,则必有f(3)(0)=6a+1=0,即,而当时,f(4)(0)＜0,从而x=0是f(x)的极大值点.

题目5(2018年高考天津卷理科第20题)已知函数f(x)=ax,g(x)=logax,其中a＞1.

思路简析问题等价于证明当时,方程组

有解,由(1)代入(2)消x1或x2.

方法1证明当a≥e1e时,关于x1的方程

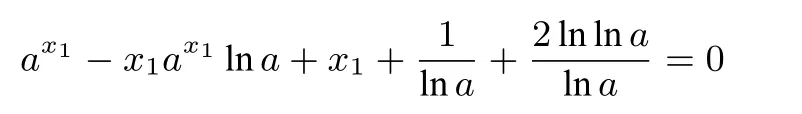
方法2证明当时,关于x2的方程lnx2-1=有实数解.令t=lnx,构造函数2,证明g(t)有零点即可.

题目 6(2018年高考江苏卷第 19题)记f′(x),g′(x)分别为函数f(x),g(x)的导函数.若存在x0∈R,满足f(x0)=g(x0)且f′(x0)=g′(x0),则称x0为函数f(x)与g(x)的一个“S点”.

(1)略;(2)略;

思路简析(3)与天津卷类似,通过构造函数说明方程有解.

评析天津卷中的(II),(III)问考的是切线平行和重合问题,这本质上考的是方程根的问题.与天津卷类似,江苏卷这道题引进一个概念“S点”,本质上是方程根的问题,也即方程有解问题.理解方程的根,可以从函数零点角度考虑.

题目7(2018年高考全国II卷理科第21题)已知函数f(x)=ex-ax2.

(1)略;(2)若f(x)在(0,+∞)只有一个零点,求a.

思路简析(2)设函数h(x)=1-ax2e-x.f(x)在(0,+∞)只有一个零点当且仅当h(x)在(0,+∞)只有一个零点.易知当a≤0时,h(x)＞0,h(x)没有零点;当a＞0时,是h(x)在(0,+∞)的最小值.根据单调性及零点定理可知当且仅当h(2)=0,即,h(x)在(0,+∞)只有一个零点.

注当h(2)＜0时,即,由于h(0)=1,所以h(x)在(0,2)有一个零点,当x＞0时,ex＞x2,所以

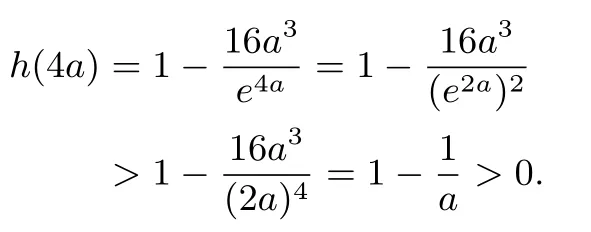
故h(x)在(2,4a)有一个零点,因此h(x)在(0,+∞)有两个零点.

寻找零点定理中零点两边异号的两个点,通常要借助于不等式放缩来找,显然这个数应该用a表示.在高等数学中通常用极限很容易说明这一点.

评析ex这种超越函数单独放在一边求导求不干净,必须跟多项式函数结合在一起,尽管这样一阶导也求“不干净”,但这样求导会有公因子ex,这样也方便找零点.代数变形,这里不直接对f(x)求导,原因在于极值点求不出来,需要求二阶导,而h′(x)=ax(x-2)e-x的零点很容易找到,这样不需要求二阶导.