圆锥曲线切线的尺规作图法

广东省佛山市罗定邦中学(528300) 龙 宇

广东省佛山市顺德区教师发展中心(528300) 王常斌

在初中阶段,我们了解到尺规作图可以做出线段的等分点,线段的垂直平分线,过一点作直线的垂线和平行线,作给定角的角平分线等.本文以尺规作图的法则作出圆锥曲线的切线.

1.圆的切线

(1)过圆上一点

如图1,过圆C上一点P作圆C的切线.

作法：设切线为l,连接CP,根据切线的性质,CP⊥l.该问题转化为过点P作CP垂线的问题.本文不再赘述.

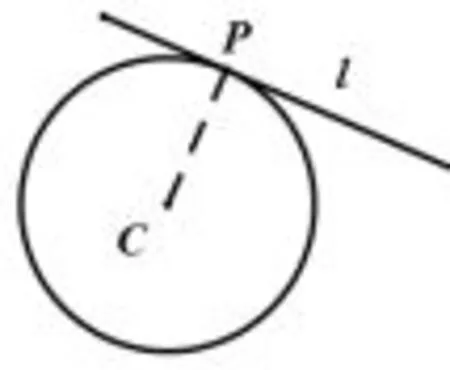
图1

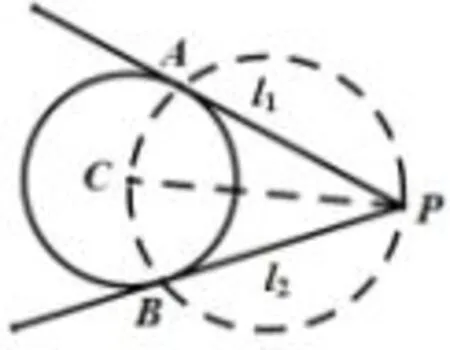
图2

(2)过圆外一点

如图2,过圆C外一点P作圆C的切线.

设过点P所作的切线为l1,l2,切点为A,B.连接CA,CB,CP.根据切线的性质,△PAC,△PBC为以CP为斜边的直角三角形.

作法：以CP为直径作圆O,圆O与圆C的交点即为切点A,B.

2.抛物线的切线

(1)过抛物线上一点

例1已知抛物线C:y2=2px(p＞0),其焦点为准线方程为设P为抛物线C上的动点,过点P作准线l的垂线,垂足为P′,连接PF.证明：过点P的切线为∠FPP′的角平分线.

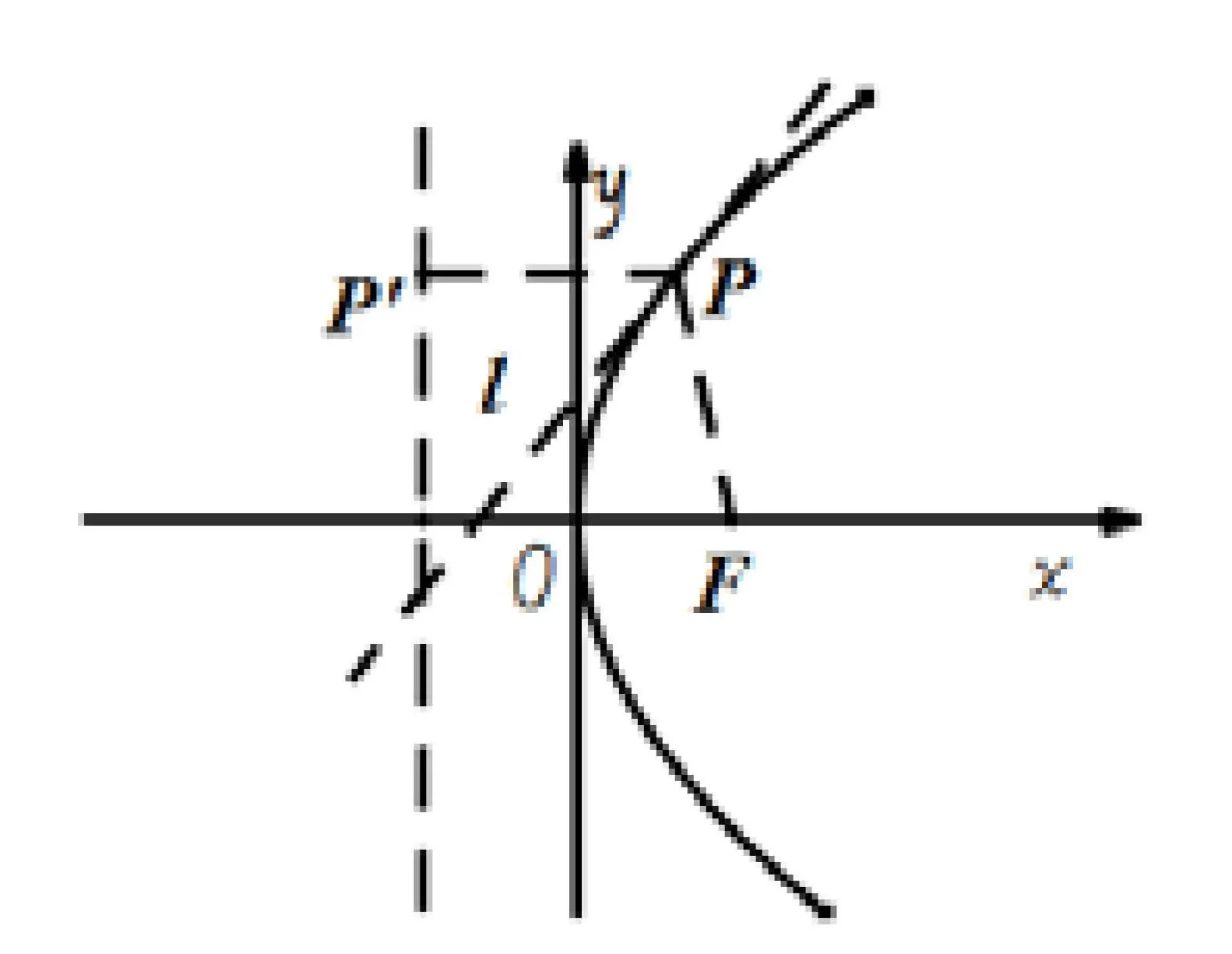
图3-1

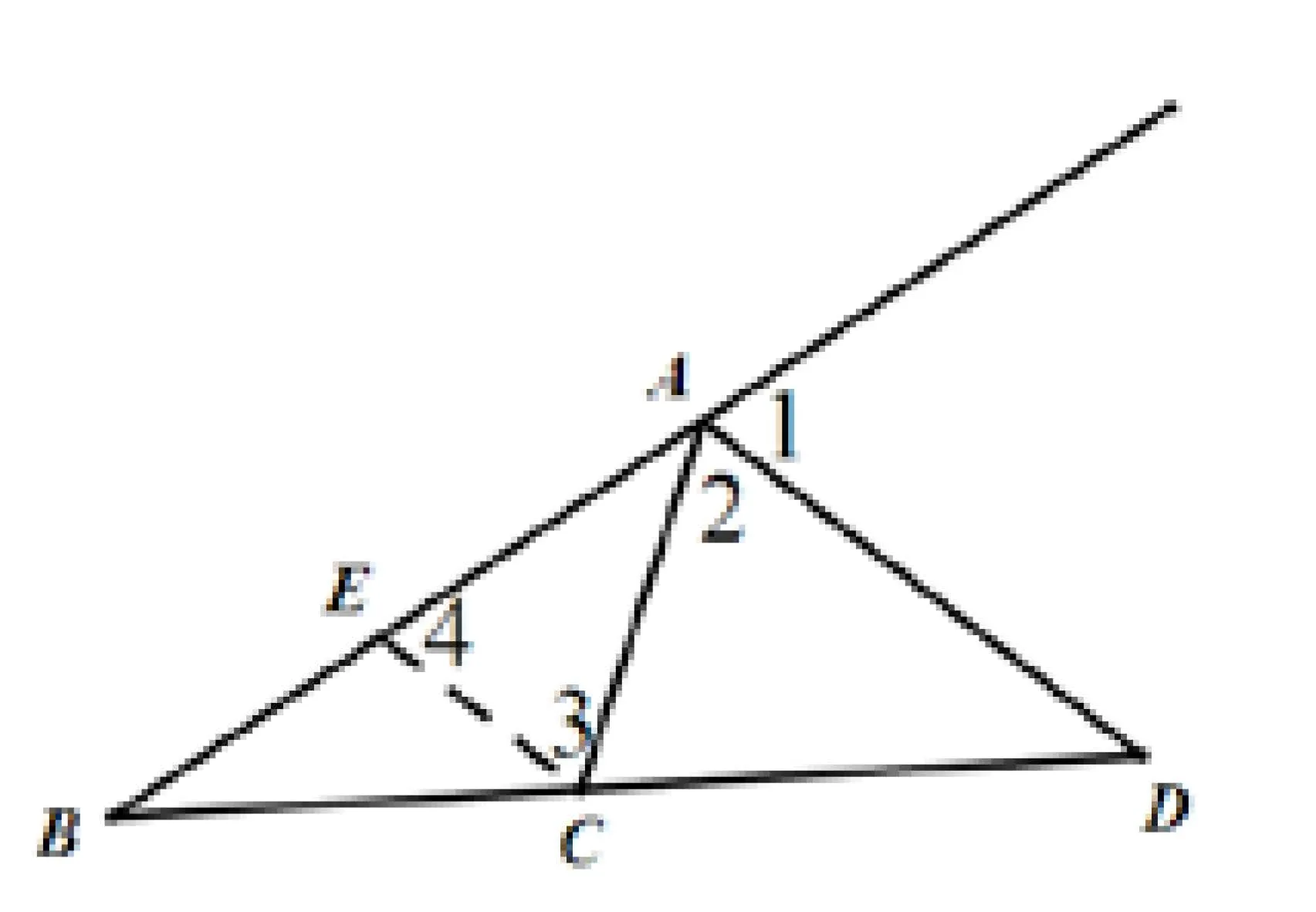
图3-2

证明(法一)如图3-1,设点P的坐标为根据文[1]可知,过点P的切线l的斜率为直线PF的斜率为.直线PP′的斜率为k2=0.设直线l到直线PF及直线PP′的夹角分别为α,β.根据到角公式：,,所以α=β.即可知过点P的切线为∠FPP′的角平分线.

(法二)引理1(外角平分线定理的逆定理)如图3-2所示,在△ABC中,若,则有AD为△ABC对应的外角平分线.

证不妨设AB＞AC(若AB=AC,则对应的点D不存在)在线段AB上找一点E,使得AE=AC,所以∠3=∠4.又因为,所以.又因为∠B=∠B,所以△BCE～△BDA,所以CE//AD,所以∠3=∠2,∠4=∠1,所以∠1=∠2,即AD可得为△ABC对应的外角平分线.

引理2设抛物线C的焦点为M,将抛物线的一条弦AD延长交准线于K,则MK平分MA与MD夹角的外角.

证过点A,D作准线的垂线交准线于 点A′,D′,所以△KDD′～△KAA′,所以根据抛物线的定义AA′=AM,DD′=DM,所以.根据引理1,即可得：则MK平分MA与MD夹角的外角.

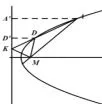
图3-3

结合切线的定义,移动点D的位置与点A重合,直线AK退化为抛物线在点A处的切线.而且当点D与点A重合时,∠AMD=0°,根据引理2,即有MK平分MA与MD夹角的外角=180°,所以MK⊥AM.由此可得如下定理：

定理1已知抛物线y2=2px(p＞0),焦点为过抛物线上一点P(x0,y0)作抛物线的切线与准线交于点K,则有FK⊥PK.

如图3-4所示：根据定理 1,∠PFK=90°,因为PP′⊥准线,所以∠PP′K=90°,即有∠PFK=∠PP′K,再有抛物线的定义,PF=PP′,且有PK作为公共边,所以△PFK∼=△PP′K,所以PK为∠FPP′的角平分线.

作图：如图3-4,根据文[2],可以通过尺规作图得到抛物线的焦点及准线.通过尺规作图完成∠FPP′的角平分线即为过点P的切线.

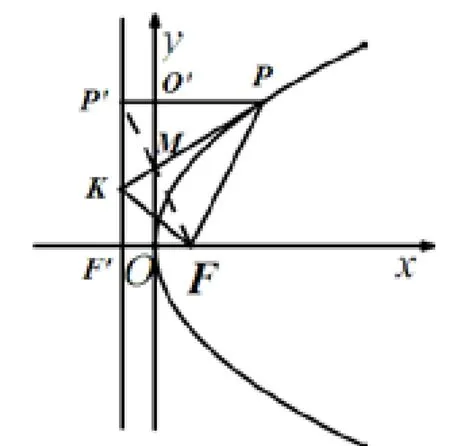
图3-4

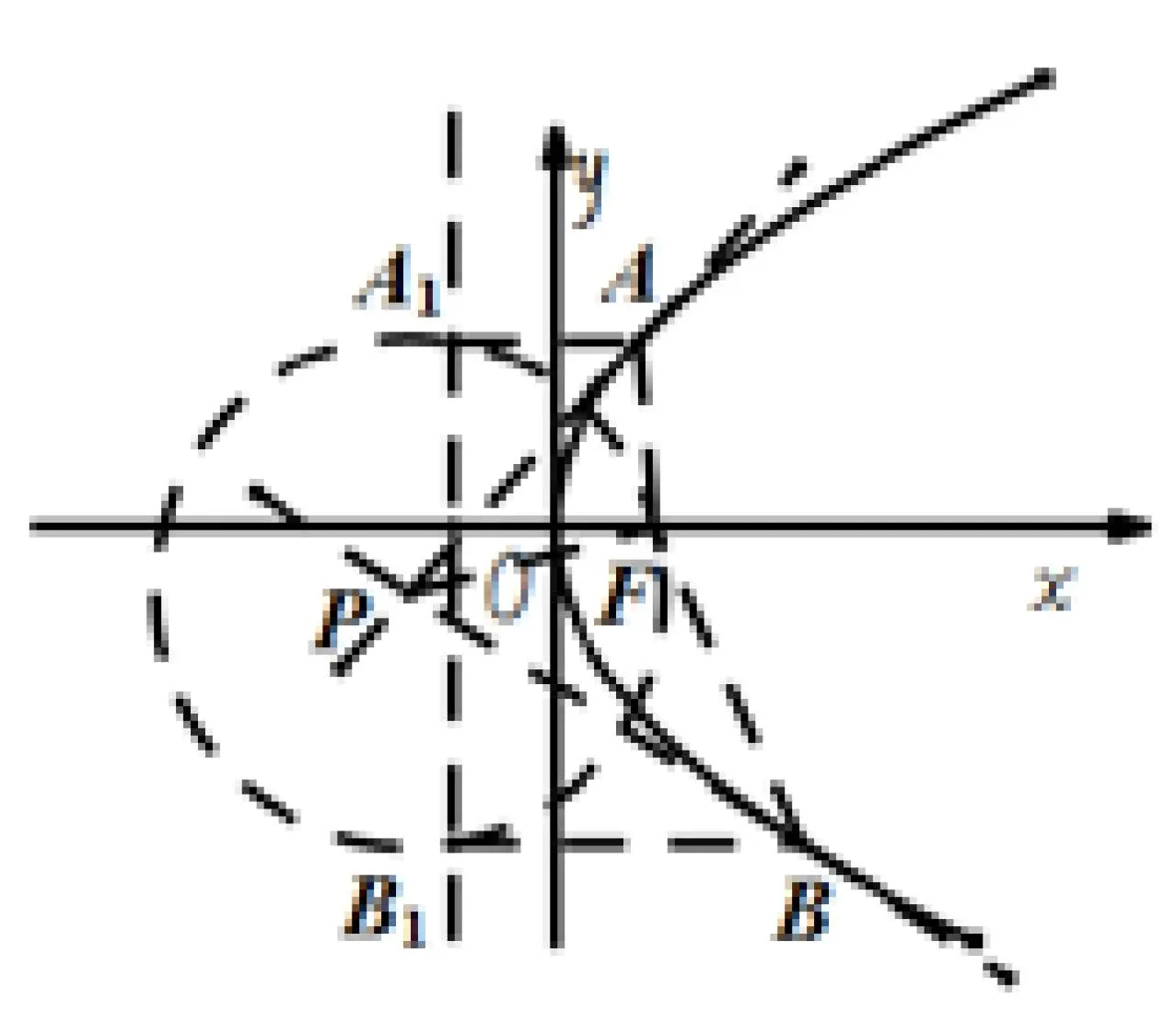
图4

(2)过抛物线外一点

如图4,过抛物线C外一点P作抛物线C的切线.

作图：以点P为圆心PF为半径作圆P,圆P与准线l的交点为A1,B1,过A1,B1分别做准线l的垂线与抛物线C相交,交点为A,B.点A,B即为对应的切点.

3、椭圆的切线

(1)过椭圆上一点

例2已知椭圆,椭圆C的左右焦点为F1,F2.点P为椭圆C上一动点,证明：过点P的切线为∠F1PF2的外角平分线.

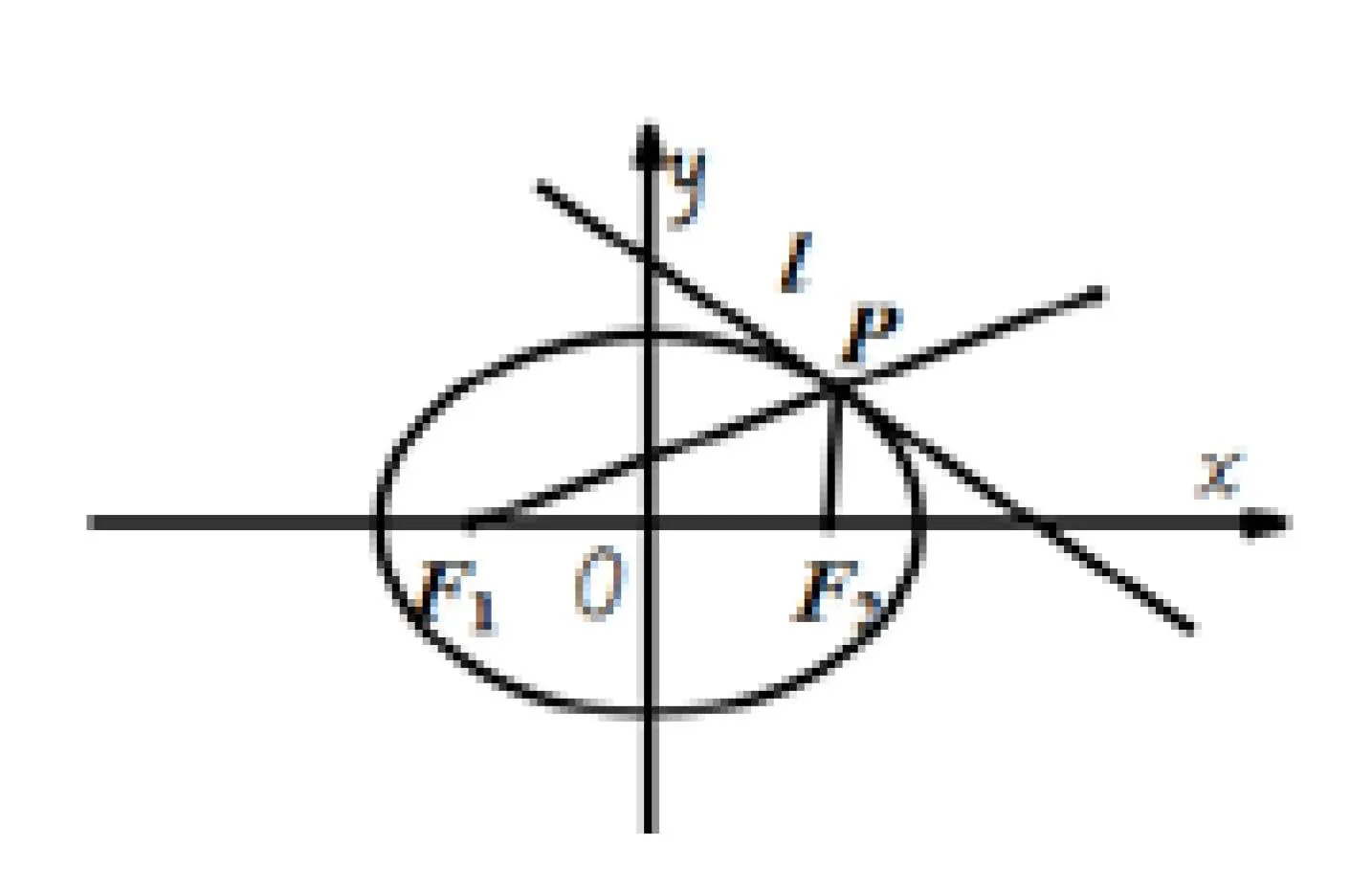
图5-1

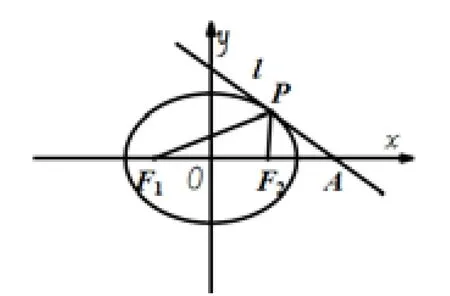
证明如图5-1,设点P的坐标为(x0,y0).根据文[1],过点P的切线方程为.当直线l与x轴无交点时,结论显然成立.当直线l与x轴的有交点时,交点为,不妨设,则有,.根据焦半径公式：,则有.根据引理1,过点P的切线为∠F1PF2的外角平分线.当x0＜0时,类似可以证明.

因为∠F1PF2的外角平分线所在的直线是唯一的,故可按以下方法作出过椭圆上一点椭圆的切线：

作图：如图5-2,延长F1P至点D,作∠F2PD的角平分线即为过点P的椭圆的切线.

(2)过椭圆外一点

例3如图6-1,已知椭圆,椭圆C的左右焦点为F1,F2.点P为椭圆C上一点,过点P作切线l,过点F1作切线l的垂线,垂足为D.证明：点D属于圆O:x2+y2=a2.

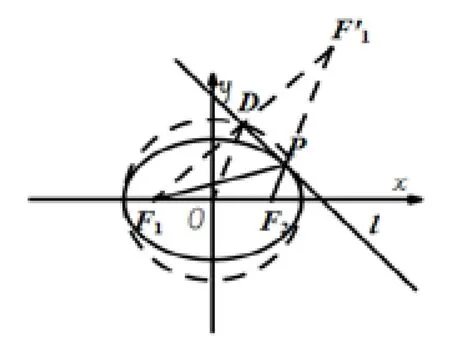
证明延长F2P与F1D交于点F′1,根据上面的结论,直线l为∠F1PF2的外角平分线.且F1D⊥l,所以△F1PF′1为等腰三角形.即有PF′1=PF1,DF′1=DF1.易知点O为F1F2的中点,所以OD为△F1F′1F2的中位线.所以点D属于圆O:x2+y2=a2.

由例3我们可以受到启发,过椭圆外一点作椭圆的切线可以如下作图：

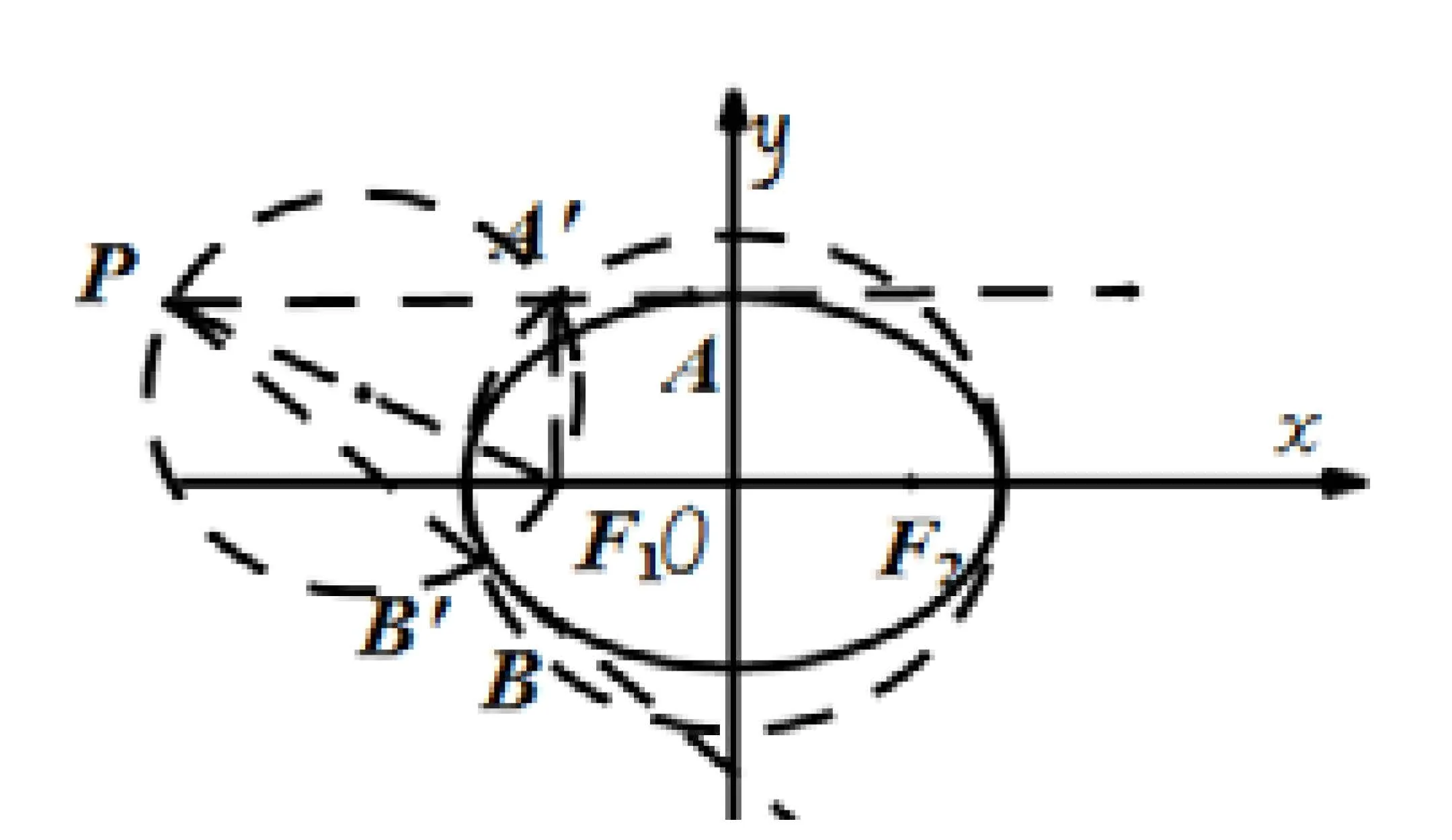
作图,如图6-2,连接PF1,以PF1为直径作圆与辅助圆x2+y2=a2交于点A′,B′,连接PA′,PB′与椭圆相交于点A,B.点A,B即为对应的切点.

以点A为例,说明如下：如图6-3,以PF1为直径作圆可得∠PA′F1=90°,即可得∠F1A′A=90°.

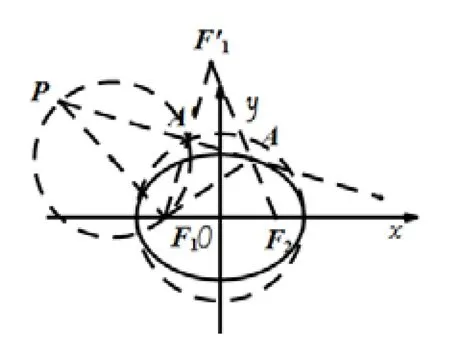
图6-3

延长F1A′至F′1,使得F1A′=F′1A′.连结F′1F2交椭圆于点A,易知A′O是△F1F2F′1的中位线.连结F1A,故F2F′1=2a=AF2+AF1,从而AF1=AF′1,由三角形全等判定边边边定理可得△AF1A′∼=△AF′1A′,从而有∠F1A′A=∠F′1A′A=90°,故P,A′,A三点共线.同时有∠F1AA′=∠F′1AA′,由例2可知,PA是椭圆的切线.

4、双曲线的切线

(1)过双曲线上一点

例4已知双曲线,椭圆C的左右焦点为F1,F2.点P为双曲线C上一动点,证明：过点P的切线为∠F1PF2的角平分线.

证明如图7,设点P的坐标为(x0,y0).根据文[1],过点P的切线方程为.设直线l与x轴的交点为.不妨设x0＞0,则有：根据焦半径公式：PF1=a+ex0,PF2=ex0-a,则有.根据角平分线定理,过点P的切线为∠F1PF2的角平分线.根据角平分线的唯一性,可以如下作图：

作图：如图7,连接PF1,PF2,做∠F1PF2的角平分线即为过点P的切线.

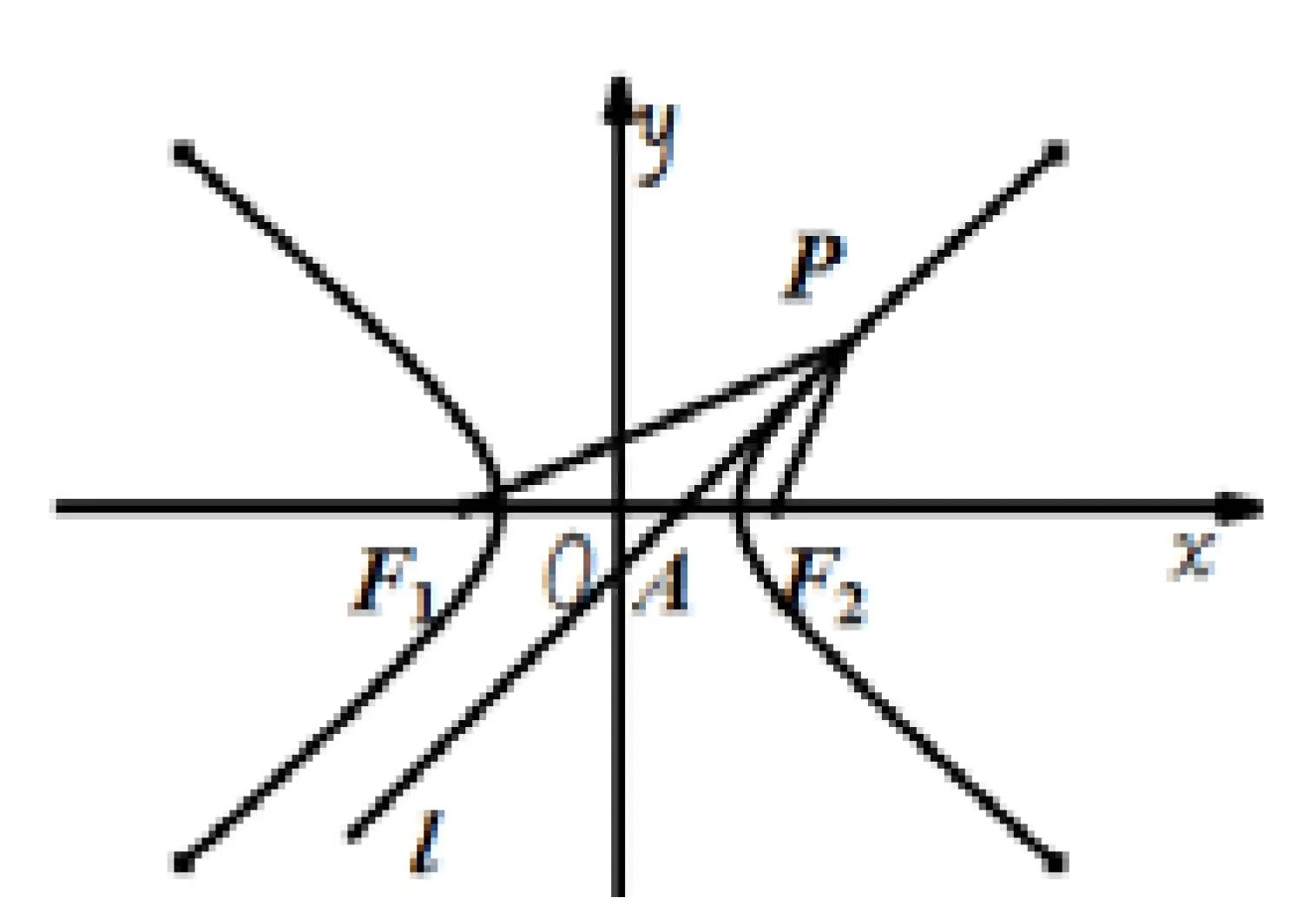
图7

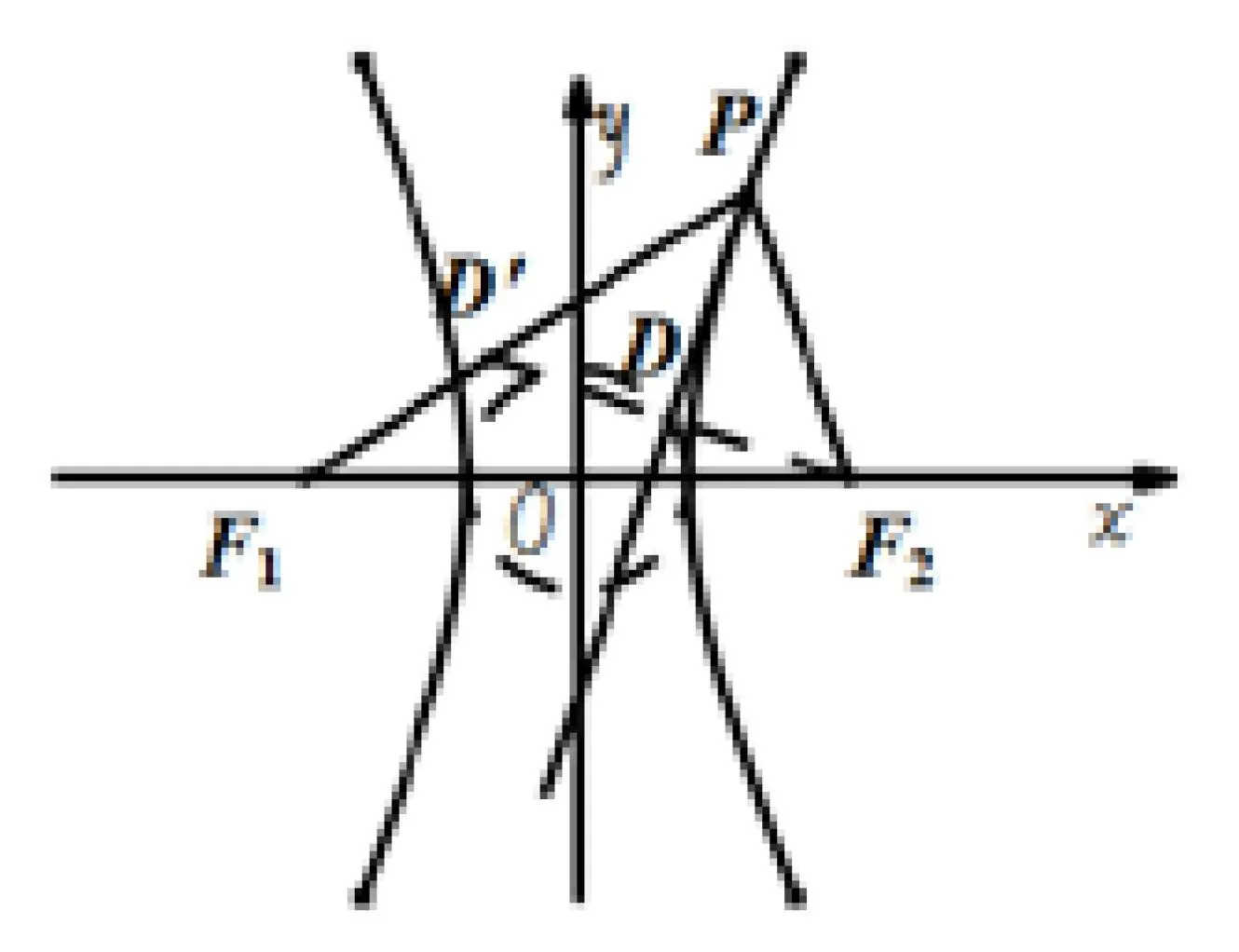
图8-1

(2)过双曲线外一点

例5如图8-1,已知双曲线,双曲线C的左右焦点为F1,F2.点P为双曲线C上一点,过点P作切线l,过点F2作切线l的垂线,垂足为D.证明：点D属于圆O:x2+y2=a2.

证明延长F2D与F1P交于点D′,根据例4,直线l为∠F1PF2的角平分线.且F2D⊥l,所以△F2PD′为等腰三角形.即有PF2=PD′,DF2=DD′.易知点O为F1F2的中点,所以OD为△F1D′F2的中位线.,所以点D属于圆O:x2+y2=a2.

作图：如图8-2,连接PF2,以PF2为直径作圆与辅助圆x2+y2=a2交于点A′,B′,连接PA′,PB′与双曲线相交于点A,B.点A,B即为对应的切点.

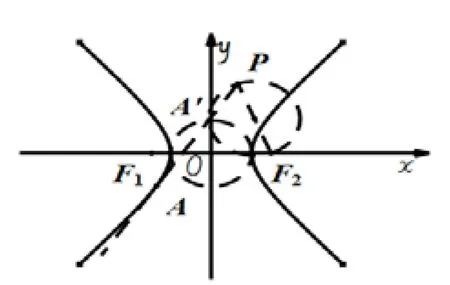
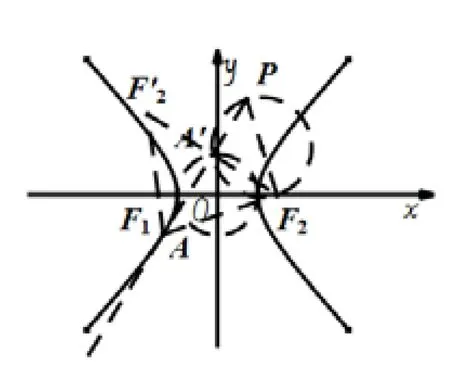
以点A为例,说明如下：如图8-3,以PF2为直径作圆可得∠PA′F2=90°,即可得∠F2A′A=90°.

延长F2A′至F′2,使得F2A′=F′2A′.,则直线PA垂直平分线段F2F′2,故有AF2=AF′2,∠F1AA′=∠F2AA′.连结F′2F1,直线F′2F1与双曲线的公共点为A,易知A′O是△F2F′2F1的中位线.连结F2A,故F′2F1=2A′O=2a=AF2-AF1=AF′2-AF1,从而A,F1,F′2三点共线.又因为∠F1AA′=∠F2AA′,由例4可知,PA是双曲线的切线.