基于航迹规划的四旋翼飞行器轨迹跟踪控制

丁 力， 柴华伟， 李兴成

(1.江苏理工学院机械工程学院，江苏 常州 213001； 2.香港理工大学工业及系统工程学系，香港 999077)

0 引言

随着机器人技术、控制技术、通信技术的发展，四旋翼被广泛应用于生产生活，如建筑现场测绘与管理、桥梁架线、电力巡线、地理建模等[1-2]。当四旋翼在城市中自主飞行时，航迹规划与飞行控制是必不可少的环节。然而与其他空中机器人一样，四旋翼具有强耦合、欠驱动、非线性的多输入多输出特性，要实现能够避障、高稳定性的飞行作业任务具有一定的难度。因此，开发高效率的航迹规划算法和高精度的飞行控制策略是工业领域和学术领域共同关注的热点。

对于航迹规划，很多学者仅简单地将无人机看作是一个质点，并采用智能算法对其进行航迹规划。例如，WANG等[3]提出一种改进的BA算法来实现无人机的三维航迹规划，并在仿真环境下获得了平滑可飞的航迹；在处理编队无人机三维航迹规划时，YANG等[4]采用自适应调整策略来改进PSO算法以避免陷入局部最优值，有效实现了无人机在三维空间中的编队飞行；SHORAKAEI等[5]提出一种并行GA算法来规划无人机的二维航迹，改进算法可处理障碍物突变问题。但上述航迹规划过程忽略了无人机的飞行力学特性，像四旋翼的姿态角对阵风干扰、机械振动等极为敏感，微小的扰动就可能会导致坠机。因此，四旋翼的航迹规划必须考虑其飞行力学特性。

对于飞行控制策略的设计，常见的方法有LQR控制[6]、PID控制[7]、H∞控制[8]等。近年来，学者们发现在稳定位姿控制的基础上，当四旋翼受到外界扰动时，其动力学模型也会发生改变。为此，所设计的控制算法必须能有效抑制未知扰动，并且具有一定的鲁棒性。例如:文献[9]提出了一种非线性自适应状态反馈控制器来补偿未知扰动，实现了四旋翼对“8”字型轨迹的跟踪；文献[10]利用扩张观测器实现对系统状态及集总干扰的准确估计，并设计级联式比例控制器保证四旋翼在低速条件下的稳定飞行。

本文另辟蹊径，针对四旋翼的航迹规划与飞行控制问题，提出了一种改进人工蜂群(IABC)算法来实现四旋翼在三维空间中的航迹规划，并引入LADRC(Linear Active Disturbance Rejection Control)控制策略来设计其位姿镇定控制器。通过IABC算法可获得最优或次优的飞行航迹，若让四旋翼简单地跟踪这些离散航点，则整个飞行过程可被视作多个阶跃信号的跟踪。根据飞行力学理论可知，这样的跟踪方式并不能满足四旋翼飞行力学特性的要求(例如相邻两航点处的速度不连续)，从而会降低四旋翼的飞行品质甚至引起其失稳。因此，本文还引入高阶多项式函数来平滑IABC算法所获得的初始航迹。最后，通过一个仿真算例验证了本文所提方法的有效性。

1 航迹规划问题描述

1.1 四旋翼的动力学模型

在四旋翼的三维航迹规划中，往往存在转向、加速、低速巡航等飞行状态，故不能忽视飞行动力学特性。而在飞行力学层面，可将四旋翼视作沿法向驱动力自由运动的单刚体模型，如图1所示。

图1 四旋翼的结构示意图Fig.1 Schematic diagram of a quadrotor

根据牛顿-欧拉法可以推导其力学方程为

(1)

(2)

1.2 障碍物建模

对于航迹规划中障碍物的建模，现有的报道大多将其简化成一个圆柱体，这样的处理一定程度上可降低规划算法的计算量。四旋翼在城市间的航迹规划，考虑到建筑物大多为长方体，本文引入长方体作为障碍物模型。对于航点P，若它在长方体内或表面上，则判断其没有避障，具体的数学实现过程如下：

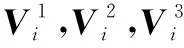
2) 计算各顶点与航点P组成矩阵的行列式值，即

(3)

3) 若矩阵D1～D5的行列式符号均相同(同为正或同为负)，则判断航点P在长方体障碍物内或表面上，不避障,否则，航点P避障。

另外，为进一步保证四旋翼的飞行安全，还需设置一个安全飞行距离l，故可将长方体障碍物的边界设为

(4)

1.3 航迹代价的建模

通常，最优的飞行航迹由航迹代价函数决定。在四旋翼飞行过程中主要考虑航程与油耗两个因素。本文利用Lagrange方程对航迹代价进行建模[13]，即

(5)

式中：CCost为航迹代价函数;C1为航程代价函数;C2为油耗代价函数;w1与w2为权重因子，本文均取为0.5;T1为时间上限。

2 航迹规划算法

2.1 人工蜂群算法

ABC算法的详细步骤如下所述。

1) 算法初始化。在解空间内，对于当前待搜索航点位置可通过式(6)随机产生xi j(i=1,2,…,N;j=1,2,…,D)组解，即随机蜜源组。

(6)

2) 收益度评价。通过式(7)来计算每个蜜源的收益度值，也就是每组航迹代价的评价值。进而，保留前N/2高评价值的航迹。

Fi=1/(1+CCosti)

>。

(7)

(8)

(9)

式中：r∈[1,2,…,N/2](r≠i)；Φi j为[-1,1]间的随机数；ω∈[ωmin,ωmax]为权重因子；T2∈[1,Tmax]为迭代次数。

4) 贪婪选择阶段。根据贪婪选择方式保留航迹代价较小的解，促使算法朝最优方向进化。

(10)

5) 跟随蜂搜索阶段。在此阶段，跟随蜂通过概率值选择雇佣蜂进行跟踪搜索。传统ABC算法中跟随蜂的选择概率与收益度值呈正相关关系，多次迭代后，会过滤掉较差的解，但这些解同样也包含着有用信息。为了保持种群多样性，本文采用如下概率选择方式，即

(11)

6) 侦察蜂搜索阶段。当更新次数超过某个阈值时，若当前蜜源不是最优解，且搜索空间中存在最优解，则放弃该蜜源，与之对应的雇佣蜂也转变成侦察蜂重新去寻找蜜源。为了提高侦察蜂对数据的挖掘能力以及避免ABC算法陷入局部最优值，本文引入立方混沌映射算子来改进其性能，如式(12)所示。这里需指出，文献[14]通过缜密的数学推理证明了立方混沌映射算子比常见的Logistic混沌映射算子具有更好的均匀遍历性与更快的收敛速度。

y(n+1)=4y(n)3-3y(n)

(12)

式中,y(n)∈[0,1]，n=1,2,…,M,M为侦察蜂的数量。将生成的混沌序列映射到侦察蜂搜索到的蜜源空间内，实现对新蜜源的混沌搜索，具体过程可参考文献[14]，这里不再赘述。

7) 最优值记录。当迭代次数达到最大值时，算法输出最优的航迹点序列以及迭代曲线。

2.2 航迹平滑

对于IABC算法优化而来的最优或次优飞行航迹，学者们都希望能以最短的时间完成全部的参考航迹跟踪，同时又能利于四旋翼姿态的控制。本文先用高阶多项式函数对IABC算法求得航点进行插值处理，得到一条光滑可飞的新航迹,进而引入速度项和加速度项建立线性规划模型，计算出最优速度序列，使得四旋翼飞行时间最优。

为了获得两航点Po与Pf之间的光滑曲线，采用高阶多项式函数(五阶多项式)进行插补计算，即

P(t)=a0+a1t+a2t2+a3t3+a4t4+a5t5

(13)

其约束条件为

上述约束条件可以确定两航点间的速度和加速度，并保证航点间的速度是连续的。

3 轨迹跟踪控制器设计

LADRC控制理论是高志强教授在韩京清教授提出的自抗扰控制基础上改进而来的[15]。与自抗扰控制相比，LADRC的扩张观测器与控制器均是线性的，并且不使用微分跟踪器，结构更为简单。另外，LADRC可将控制器参数降到3个，即观测器ωo、控制器带宽ωc及增益b0。观察四旋翼的动力学模型(式(2))可知，位置与姿态的状态变量分别与控制输入呈二阶导数关系，故可以设计6个二阶LADRC控制器分别镇定四旋翼的位置环与姿态环。

3.1 二阶LADRC控制原理

不失一般性的，对于一个二阶被控对象

(14)

式中：x为系统的状态变量；u为系统的输入；y为系统的输出量；w为系统的扰动量。

(15)

式中：b0为b(t)的估计值。因此，有

(16)

(17)

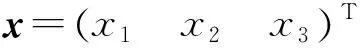
采用线性扩张观测器对式(17)进行观测，则有

(18)

(19)

3.2 四旋翼轨迹跟踪控制框图

根据时间尺度原理，可将四旋翼的动力学模型分为位置与姿态两个控制环，并分别设计二阶LADRC控制器，如图2所示。其中，(Xr,Yr,Zr)为参考轨迹，(φr,θr,ψr)为控制过程中产生的中间姿态参考值。

图2 四旋翼位姿控制框图Fig.2 Position and attitude control for a quadrotor

4 仿真分析

本章通过一个仿真算例来验证所提基于IABC算法的四旋翼三维航迹规划以及基于LADRC的轨迹跟踪控制的有效性。设置仿真环境为：飞行空间为12 m×8 m×10 m ，环境中存在4个长方体障碍物；飞行的起始位置为(1 m,-4 m,1 m)，目标位置为(8 m,7 m,5 m)，安全飞行距离l=0.1 m；飞行要求为从起始点位置到目标位置的航程短且避障、飞行耗时少；四旋翼的质量m=0.2 kg，臂长为0.1 m，转动惯量为Ixx=Iyy=2×10-4kg·m2，Izz=3.7×10-4kg·m2；偏航角设为ψr=0 rad。

整个仿真过程分为两步：1) 用寻优算法找出一条航迹代价值最小的航迹，并对其进行平滑处理；2) 将处理后的平滑航迹作为飞行控制器的参考轨迹，通过LADRC控制器实现对参考轨迹的跟踪。设置IABC算法的仿真条件为：N=30，llimit=5。同时，分别引入ABC算法和GA算法来比较IABC算法的性能。ABC算法的条件与IABC算法相同，GA算法的仿真条件为：抗体种群数为30，交叉因子与变异因子分别为0.8与0.2。考虑到航迹规划的时效性，设置3种算法的迭代总次数为20。另外，每种算法均重复10次，记录下每次的规划效果，并取其中最优结果作为参考。

航迹规划的效果如图3和图4所示。从图中可以看出，3种算法均能为四旋翼规划出一条安全避障的飞行轨迹，但这些轨迹不可飞；高阶多项式函数对规划的轨迹进行了插值处理，使得轨迹平滑可飞。相比而言，IABC算法规划的效果最好。这表明IABC算法对数据的开采能力更强。图5给出了3种算法迭代曲线，可以看出,IABC算法的收敛速度明显高于ABC算法与GA算法，且能够挖掘到更好的解。这表明改进后的ABC算法无论在收敛速度上还是数据挖掘上都有很大的性能提升。

图3 3D航迹规划结果Fig.3 3D path planning result

图4 XY平面内的规划效果Fig.4 Result of path planning in XY plane

进一步地，表1给出了3种算法的寻优性能指标对比。从表中可以看出，IABC算法规划的航迹长度是最短的，分别比ABC算法、GA算法缩短了0.9%和3.18%。由于IABC算法中引入了自适应策略、新的概率选择方式及立方混沌搜索算子，其优化效率不及ABC算法，且优化成功率也低于后者。但总体来讲，80%的成功率还是说明IABC算法具有较高的可靠性。

表1 3种算法的性能指标对比

表2给出了3种航迹平滑后的性能指标对比。从表2中可以看出，经平滑后IABC-1获得的航迹长度还是最短的，飞行时间也最少，并且能够有效避障。

表2 3种航迹平滑后的性能指标对比

将平滑处理的航迹IABC-1作为四旋翼的参考轨迹，并在测量端添加幅值为0.05的随机扰动。在二阶LADRC控制器的作用下，四旋翼的三维轨迹跟踪效果如图6和图7所示。从图中可以看出，位置控制器基本上可以跟踪参考轨迹。由于扰动的存在，前期的跟踪超调比较大，但是LADRC还是可以迅速地抑制扰动，减小跟踪误差。

图6 三维轨迹跟踪结果Fig.6 Result of 3D trajectory tracking

图8和图9给出了俯仰角和横滚角的响应曲线，姿态角的参考值由位置环给出。从图中可以看出，俯仰角和横滚角均在1 s左右跟踪上参考值，可以满足四旋翼实际操控的需求。另外，两个姿态角的稳态误差均能够保持在±0.02 rad内。这表明LADRC控制器鲁棒性强、响应速度快及控制精度高。

图7 XY平面内跟踪轨迹Fig.7 Tracking trajectory in XY plane

图8 俯仰角的响应Fig.8 Response of pitch angle

图9 横滚角的响应Fig.9 Response of roll angle

5 结论

提出了一种改进的人工蜂群算法来实现四旋翼的航迹规划。算法中，在雇佣蜂搜索阶段引入自适应策略、跟随蜂搜索阶段引入一个新的概率选择方式、侦察蜂搜索阶段引入立方映射混沌算子来提高收敛速度，避免陷入局部最优值。

根据四旋翼动力学特性，设计位置环与姿态环二阶LADRC控制器。以高阶多项式函数平滑后的航迹为参考轨迹，实现高精度的抗干扰轨迹跟踪控制。

仿真结果表明，IABC算法的迭代速率、规划结果均优于ABC算法与GA算法，改进后的ABC算法具有更强的数据挖掘能力与鲁棒性；所设计的二阶LADRC控制器能够有效抑制扰动，使四旋翼快速跟踪上参考轨迹。