含旋转铰间隙平面运动机构可靠性灵敏度分析

刘付超，魏鹏飞，周长聪，张政，岳珠峰

西北工业大学 力学与土木建筑学院，西安 710129

运动机构是设计用来实现预定运动输出，进而实现特定功能的机械装置，在航空领域中有普遍的应用。其中，平面机构各构件之间必须通过连接以实现运动传递。不可避免的是，伴随着杆件连接处的不断磨损或腐蚀，构件连接间隙不断扩大，此外，杆件在加工过程中也会出现尺寸误差，种种因素导致机构实际运动输出与理想运动输出并不完全切合，即会产生一定程度的运动误差。研究运动误差是否始终不超过误差极限的问题即称为“动态可靠性分析”[1]。其中包含两大方面，一是在区间内各点或整个区间段上对运动机构的可靠性进行分析；其次是确定影响机构运动失效的误差来源，即灵敏度分析。对于区间内各点的可靠性分析，目前已经发展出许多成熟的算法，例如一阶可靠性方法[2-3]、二阶可靠性方法[4]、重要性抽样方法[5]、线性抽样方法[6]，都可以解决类似问题。对于整个区间的时变可靠性分析，Rice首先提出了首超法[7],并取得了广泛的应用[8-11];其次，杜小平通过对误差函数的一阶近似估计和包络函数法，发展出一种数值近似方法[12],使得计算精度大大提高。其他时变可靠性分析方法还包括密度函数演变法[13]、最大熵法[14]，等等。

可靠性灵敏度分析包括局部灵敏度分析和全局灵敏度分析。局部灵敏度分析为失效概率对随机输入变量分布参数的偏导数，意为随机输入变量分布参数的波动对于失效概率的影响程度。对于静态结构，文献[15-17]已有成熟的局部灵敏度计算方法；对于运动机构，一点处的局部灵敏度分析已经实现[18]，更进一步，魏鹏飞等完成了全区间段内局部灵敏度分析[19]。与之相对应，全局灵敏度分析旨在确定任意随机输入变量对于输出结果不确定性的影响[20-23]。经过不断的发展，许多成熟的全局灵敏度分析方法得到了实现，例如基于方差的全局灵敏度分析方法[24]，矩独立全局灵敏度分析方法[25-26]，以及基于抽样的全局灵敏度分析方法[27]等等。

就目前所知，当前还没有对含旋转铰间隙平面运动机构进行全局灵敏度分析的研究工作。然而旋转铰间隙几乎存在于所有运动机构，并且对机构的运动精度产生不可忽视的影响。对含旋转铰间隙平面运动机构进行全局灵敏度分析，可以有效地提高机构可靠性，具有重要的研究意义和应用价值。本文首先明确该种运动机构的全局灵敏度指标定义，其次结合相关运动机构模型，构造其运动误差的包络函数，在此基础上建立含旋转铰间隙平面运动机构的全局灵敏度计算方法。最后，通过两个具体算例验证所提方法的有效性和可行性。

1 全局灵敏度指标定义

假定运动机构误差函数为g(X,θ)，X=(X1,X2,…,Xn)为机构参数输入变量，θ为时间因素输入变量,误差极限为ε。则运动机构安全域定义为

S=X:g(X,θ)≤ε

(1)

定义安全域S指示函数为

(2)

对于指示函数IS的方差可分解为[21]

∑i≠j≠kVijk+…+V1,2,…,n

(3)

从中分离出主方差贡献Vi，二阶方差贡献Vij，以及总方差贡献VTi。

主方差贡献定义为

Vi=V(IS)-EV(ISXi)

(4)

式中：EV(ISXi)为变量Xi固定后，其他变量对于指示函数方差的贡献，则Vi可理解为变量Xi固定后，方差V(IS)的减小量。

二阶方差贡献定义为

Vij=VE(ISXi,Xj)-Vi-Vj

(5)

式中：VE(ISXi,Xj)为变量Xi、Xj对方差V(IS)的整体贡献，则Vij为变量Xi、Xj两者之间的相互作用对整体方差V(IS)的贡献。

总方差贡献定义为

V1,2,…,n=EV(ISX:i)

(6)

式中：X:i为变量X中除去Xi以外的n-1维向量，进而，VTi可理解为除变量Xi外，其他变量全部固定后，变量Xi对整体方差V(IS)的贡献。

进而，通过以上3种方差贡献定义出相应的全局灵敏度指标：

(7)

(8)

(9)

为了考察高阶方差贡献，利用以上3种指标对高阶指标SHi进行定义：

(10)

2 全局灵敏度方法

2.1 含旋转铰间隙平面运动机构模型及运动误差函数

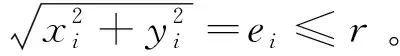
Y=Y(X,θ)

(11)

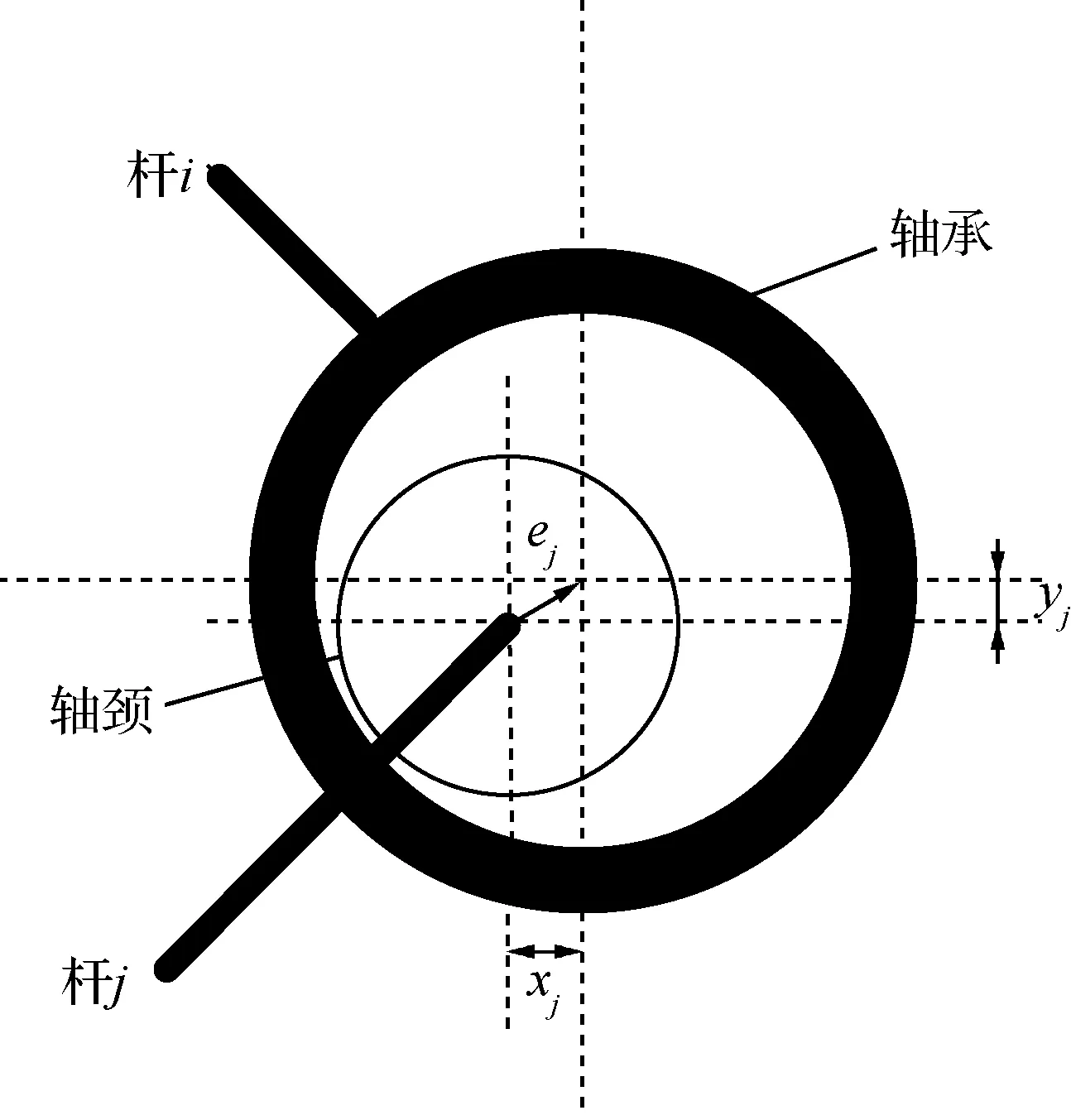
图1 连接间隙Fig.1 Joint clearance

以Y0表示理想运动输出，则运动误差函数可表示为

g(X,θ)=Y(X,θ)-Y0(θ)

(12)

2.2 基于包络函数的可靠性分析

机构区间可靠性定义为：对于任意θ属于θs至θe，运动误差函数g(X,θ)的绝对值不大于误差极限ε的概率，即

R(θs,θe)=Pr{max(g(X,θ))≤ε∩

ming(X,θ)≥-ε}

(13)

对误差函数g(X,θ)进行进一步简化[28]：

g(X,θ)≈H(U,θ)=b0(μX,θ)+b(μX,θ)·U

(14)

式中：

(15)

并且

(16)

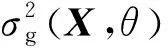
μgX,θ≈b0μX,θ

(17)

(18)

定义指示函数为

(19)

进而可靠性表达式可简化为

R(θs,θe)=Prmaxs(θ)H(U,θ)≤ε

(20)

考察机构在某一区间内的可靠性，可选取区间内某些最易失效点组成联合密度函数，进而对其进行积分得出机构可靠性指标，此即为包络函数法。

构造包络函数G(X),使得

(21)

求解包络函数G(X)，得出最可能失效点θi(i=1,2,…,t)，进而构造出误差函数的均值向量为

μH=(μg1,μg2,…,μgt)

(22)

以及协方差矩阵：

(23)

其中，μgii=1,2,…,t为误差函数在各失效点θi处的均值。Covij为g(X,θi)和g(X,θj)的协方差，i,j=1,2,…,t，具体形式为

(24)

含旋转铰间隙平面运动机构可靠性表达式为

(25)

2.3 含旋转铰间隙平面运动机构全局灵敏度分析

在第1节中已经对主指标、高阶指标以及总指标进行了定义。因为X为随机向量，则IS(X)为随机变量，且由式(2)可知，IS(X)服从两点分布B1,R，即IS(X)等于1的概率为R，等于0的概率为1-R，因此，IS(X)的方差可以表示为

V(IS)=R(1-R)

(26)

为进一步方便对各全局灵敏度指标的计算，对Vi、Vij、VTi做推导[19]：

Vi=VE(IS|Xi)=EE2(IS|Xi)-R2

(27)

Vij=VE(IS|Xi,Xj)-Vi-Vj=

EE2(IS|Xi,Xj)-R2-Vi-Vj

(28)

VTi=EV(IS|X:i)=V(IS)-

V[E(IS|X:i)]=R-EE2(IS|X:i)

(29)

故只需求得EE2(ISXi),E[E2(ISXi,Xj)],E[E2(ISX:i)]，便可得到相应的全局灵敏度指标。

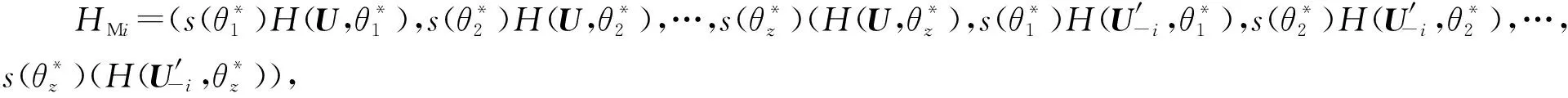
(30)

式中：μHMi和ΣHMi分别为HMi的均值向量和协方差矩阵。

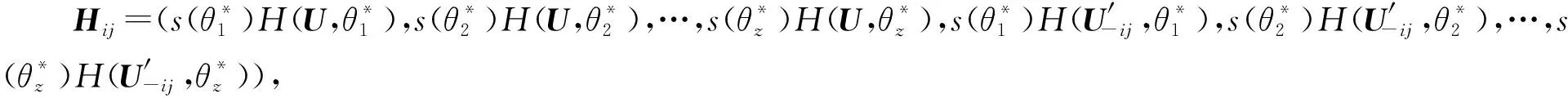
(31)

式中：μHij和ΣHij分别为Hij的均值向量和协方差矩阵。

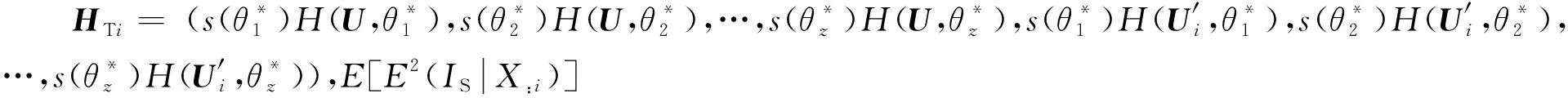
(32)

式中：μHTi和ΣHTi分别为HTi的均值向量和协方差矩阵。

进而，将式(27)～式(29)和式(30)～式(32)相结合，代入式(7)～式(9)中，可分别求得全局灵敏度主指标、高阶指标和总指标。公式的具体推导过程可参考文献[19]。

3 算 例

3.1 四连杆机构

四连杆机构在航空领域有极大的应用[29]，考虑某四连杆机构如图2所示，1杆为驱动杆，1杆、3杆与水平线夹角θ、ψ分别为输入变量、输出变量。杆长服从正态分布，均值μ=(52.2,104.9,67.6,100)，标准差均为0.1；间隙尺寸(xj,yj)，j=1,2,3,4，在半径为0.02的圆内服从均匀分布，理想输出函数

(33)

式中：f(x)=sinx，x∈[0, 90°]；初始输入、输出变量分别为θ0=95.1°、ψ0=90.6°，变化范围分别为Δθ=120°、Δψ=60°。误差极限ε取0.23°和0.25°。考察4根杆L1、L2、L3、L4以及4个连接间隙C1、C2、C3、C4的全局灵敏度。以X1,X2,…,X8表示为X1=L1,X2=L2,X3=L3,X4=L4,X5=C1,X6=C2,X7=C3,X8=C4。

根据图2可建立等式

(34)

消去ψ可得机构实际运动输出方程为

(35)

当误差极限取0.23°和0.25°时，主指标、总指标、高阶指标计算结果分别展示于图3和图4当中，并与蒙特卡罗法计算结果相比较，蒙特卡罗法样本点数为106。

当误差极限取0.23°时，由蒙特卡罗法计算出的失效概率为：Pf=0.076 004。蒙特卡罗法程序运行时间为382 s，而本文所提方法程序运行时间为64 s，原误差函数调用次数为245次，各项指标计算结果如图3所示，其中，S,ST,SH分别代表主指标、总指标和高阶指标，S1,S2,…,S8分别为各输入变量主指标，ST1,ST2,…,ST8分别为各输入变量总指标，SH1,SH2,…,SH8分别为各输入变量高阶指标。由图3(a)可知，在所考察的8个变量中，X2和X4的主指标明显高于其他各因素,由此说明，通过降低X2与X4的不确定性，可以使得结构的可靠性显著提升。相反，其他各因素主指标对结构可靠性方差贡献普遍微弱。由图3(b)可以看出，相比于主指标计算结果，各因素总指标均有大幅度提升，说明各因素间相互作用明显存在，其中，尤以X2和X4显著。通过图3(b)与图3(c)对比可以发现，X5、X6、X7、X8的高阶指标与总指标存在着微弱的差距，这也从另一个方面表明X5、X6、X7、X8的主指标与二阶指标几乎为零。

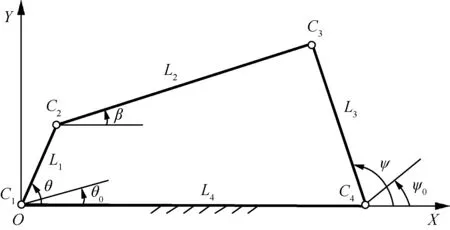
图2 四连杆机构Fig.2 Four-bar linkage

当误差极限取为0.25°时，由蒙特卡罗法计算出的失效概率为：Pf=0.0 256 045，各项指标计算结果如图4所示。由图3和图4可以看出，随着误差极限的增加、失效概率的下降，主指标普遍下降、总指标和高阶指标均微弱增长。由此说明，随着机构可靠性的增加，每个因素对于时变可靠性的单独影响减小，整体影响以及各因素间相互影响普遍增加。通过对比图3和图4同样可以发现，机构可靠性的变化对各输入变量的灵敏度指标排序并没有影响。计算成本方面，蒙特卡罗法程序运行时间为382 s，而信封函数法程序运行时间为66 s，且原误差函数调用次数为245次，表明信封函数法计算效率高，成本小。

图3 误差极限为0.23°时四连杆机构全局灵敏度分析结果Fig.3 Results of global sensitivity analysis of four-bar linkage when error limit is 0.23°

图4 误差极限为0.25°时四连杆机构全局灵敏度分析结果Fig.4 Analysis of global sensitivity analysis of four-bar linkage when error limit is 0.25°

3.2 某转向机构

考虑某转向机构如图5所示，Lb代表左侧1操纵臂和右侧4操纵臂的长度，Ls代表左侧2转向连接杆和右侧3转向连接杆的长度，W表示下侧轮轴长度，H为轮轴与齿条轴5之间的距离。以齿条轴5的横向位移D为输入变量，左侧操纵臂与水平线夹角θ1为输出变量。X=(X1,X2,X3,X4)=(Lb,Ls,W,H)代表4个随机尺寸变量，均值μ=(111,283.5,650.24,83.5) 10-3m，标准差为σ=(0.1,0.1,0.1,0.1) 10-3m。间隙变量(xj,yj),j=1,2，在半径为0.1的圆内服从均匀分布。机构理想运动输出假定为实际运动输出函数在尺寸变量和间隙变量均值处的取值。考察4个尺寸因素Lb、Ls、W、H以及2个间隙因素C1、C2的全局灵敏度。分别以X1,X2,…,X6表示为:X1=Lb,X2=Ls,X3=W,X4=H,X5=C1,X6=C2。

根据图5可得等式：

(36)

消去θ2可得机构实际运动输出方程为

(37)

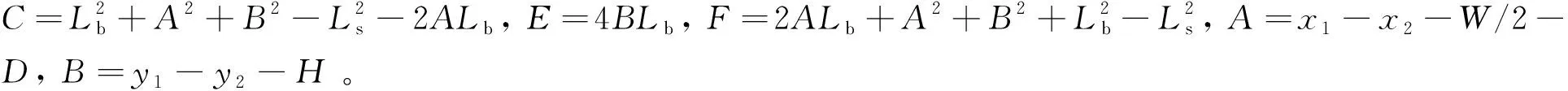
当误差极限取0.4°时，主指标、总指标、高阶指标计算结果展示于图6当中。蒙特卡罗法样本点数为106。

当误差极限取0.4°时，由蒙特卡罗法计算出的失效概率为：Pf=0.0 663 576。蒙特卡罗法程序运行时间为248 s，信封函数法程序运行时间为43 s，原误差函数调用次数为245次。由图6(a)可知，所考察的6个变量的主指标普遍较小，由此也导致两种方法的计算结果在图像上存在明显的相对差异，但通过比较可知，绝对偏差较小，所提方法依旧具有足够的准确度。从图中可以看出，相比于其他4个因素，X1和X2具有较高的主指标，由此说明，对各输入变量均降低一定程度的不确定性，相对于其他输入变量，X1和X2可使结构的可靠度得到更多的提高。由图6(b)可以看出，各因素总指标相对于主指标均有大幅度提升，这也使得两种方法的计算结果具有更高的贴合度，同时说明各输入变量间具有明显的相互作用。在全部输入变量中，X1、X2具有较高的总指标，其次为X5、X6，值得注意的是，两个间隙因素X5、X6具有相同的总指标，说明两因素整体上对机构可靠性具有相同影响。在图6(b)与图6(c)的对比中可以发现，各输入变量高阶指标与总指标间具有明显的差距，且由图6(a)可知各变量主指标较小，从而表明各输入变量两两之间具有显著的相互作用。

图5 某转向机构示意图Fig.5 Diagram of a steering gear

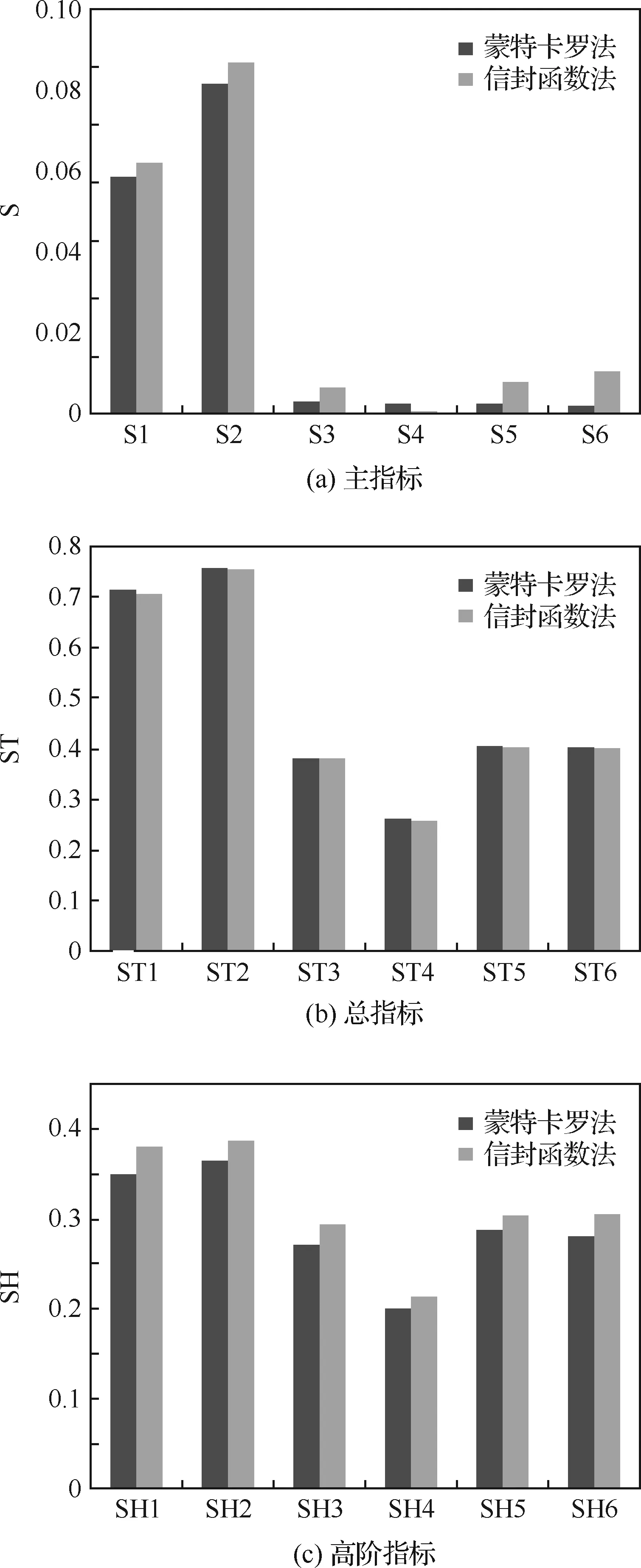
图6 某转向机构全局灵敏度分析结果Fig.6 Results of global sensitivity analysis of steering gear

4 结 论

1) 对于含旋转铰间隙的平面运动机构，本文在时变运动机构可靠性灵敏度分析方法的基础上，结合包络函数法，发展出一种高效的计算含旋转铰间隙平面运动机构全局灵敏度的分析方法。

2) 将本文所发展的高效计算方法应用到两个实际算例中，并与蒙特卡罗法相对比，结果显示，本文所提方法所得结果与蒙特卡罗法所得结果非常接近，程序运行时间大大缩短，且误差函数调用次数较少，表明本文所提方法精确度高，计算成本小，具有良好的工程应用价值。