基于MCFT的钢筋增强ECC梁受剪承载力计算方法

乔 治 潘钻峰 梁坚凝 孟少平

(1东南大学土木工程学院,南京 210096)(2同济大学土木工程学院,上海 200092)(3香港科技大学土木与环境工程系,香港)

混凝土构件的剪切破坏属脆性破坏,其受剪性能与混凝土材料本身的抗拉性能息息相关.Li等[1-2]根据细观力学和断裂力学设计出具有应变硬化能力的超高韧性水泥基复合材料(ECC),在纤维体积掺量不大于2.0%的情况下,其极限拉应变可达到2%以上,且拉伸过程中形成许多相互平行的宽度小于100 μm的细裂缝.国内外学者对ECC构件的受剪性能进行了一定的研究,研究成果均表明[3-12],ECC材料优异的拉伸延性能够提高构件的受剪承载力和剪切延性.

文献[13-17]将MCFT改进后用于高性能钢纤维混凝土构件受剪承载力的计算中,取得了较好的预测精度.相比传统混凝土材料和钢纤维混凝土材料,ECC开裂后表现出明显的应变硬化现象,能够继续承担拉应力,因此开裂后的ECC更适合被看作一种连续材料而应用到MCFT理论中.Xoxa[6]利用面内纯剪试验数据拟合了ECC平均主拉应力应变关系和裂缝处局部应力平衡关系,并提出了适用于ECC构件受剪承载力计算的修正MCFT理论.Nagai等[18]根据已有试验资料,得到了ECC在拉压双轴应力状态下的软化单轴拉伸应力应变关系和软化单轴压缩应力应变关系,以用于模拟开裂后ECC材料的力学行为.

本文基于ECC材料力学特性,修正了MCFT中材料的软化平均应力-应变关系,为考虑纤维在斜裂缝处的应力传递能力,对MCFT中的局部应力平衡方程也做出相应调整,使该理论能够更好地反映钢筋增强ECC(RECC)梁的受剪机理;然后通过合理简化,推导了ECC斜裂缝角度和平均主拉应变的显示计算公式,并提出了有腹筋RECC梁受剪承载力的简化计算方法.建立了40根RECC梁和6个RECC板的剪切试验数据库,对本文提出的修正MCFT方法和简化计算方法进行了验证.

1 基于MCFT的RECC梁抗剪计算模型

1.1 变形协调方程

假定钢筋与基体材料之间形变完全协调,并将开裂后的ECC看作新的材料,采用跨越几条裂缝的平均应力应变，并借助莫尔圆建立了相容方程.图1为RECC梁单元体平均应变莫尔圆,由图可得

γxy=2(εx-ε2)/tanθ

(1)

εx+εy=ε1+ε2

(2)

(3)

式中,ε1,ε2分别为垂直于裂缝的平均主拉应变和平行于裂缝的平均主压应变;εx,εy,γxy分别为平均纵向应变、平均横向应变、平均剪切应变;θ为裂缝(或斜压杆)倾角,为简化计算,假定裂缝倾角与主压应力及应变方向一致.

图1 开裂ECC单元的变形协调示意图

1.2 平衡方程

RECC梁单元体受力状态及其相应的ECC平均应力莫尔圆见图2,由图可得以下方程式:

fx-ρsxfsx=fcx=f1-νxy/tanθ

(4)

fy-ρsyfsy=fcy=f1-νxytanθ

(5)

f2=f1-vxy(tanθ+cotθ)

(6)

式中,fx,fy分别为单元体x和y方向的应力;fsx,fsy分别为钢筋x和y方向的应力;fcx,fcy分别为ECC材料x和y方向的应力;f1,f2,νxy分别为ECC平均主拉应力、平均主压应力及平均剪应力;ρsx,ρsy分别为单元体x和y方向的配筋率.

(a) 力平衡方程

1.3 本构方程

ECC构件斜向开裂后,ECC斜压杆处于拉压双轴应力状态,这使得ECC在主压应力和主拉应力方向上均发生明显的软化现象.Xoxa[6]根据ECC面内纯剪试验数据回归分析，得到了开裂ECC考虑受拉软化效应的平均主拉应力(f1)-应变(ε1)关系:

(7)

Nagai等[18]为考虑ECC斜压杆在受压方向的软化现象,提出在ECC单轴受压应力-应变曲线上乘以一个软化系数ωc,则开裂ECC的主压应力(f2)-应变(ε2)关系可表达为

(8)

(9)

式中,εtu为ECC的极限拉应变;εc为ECC的峰值压应变;κ为形状系数,对于混凝土材料κ=2,对于ECC,κ可近似取为1.35.

1.4 裂缝间及裂缝处力的平衡方程

RECC梁在斜裂缝之间的应力传递如图3所示.不同于普通钢筋混凝土梁,RECC梁出现斜裂缝后,裂缝间ECC所承担的拉应力并不会减小,反而会随着外力的增加而继续缓慢增加,裂缝处的ECC由于纤维的桥接作用同样存在一部分拉应力.在斜裂缝之间与斜裂缝处,梁所承受的剪力分别为

(10)

(11)

式中,b为截面宽度;dv为计算模型的抗剪有效高度,可近似取max(0.9h0,0.72h)[19-20],h0为截面有效高度,h为截面高度;fscry为裂缝处的钢筋应力;Asy为配置在同一截面内箍筋各肢的截面面积;s为沿构件长度方向的箍筋间距;vci为裂缝面上骨料咬合作用产生的剪应力;fcr1为裂缝处的纤维桥接应力,Xoxa[6]给出了一个基于纯剪试验数据的回归公式:

(12)

Collins等[21]忽略裂缝间压应力的有利作用,得到混凝土开裂面所能传递的最大剪应力为

(13)

式中,ag为骨料的最大尺寸;ω为斜裂缝宽度,可近似表示为[22]

(14)

式中,sy和sx分别为箍筋间距和腹板中纵筋的竖向间距,sy和sx的取值均应大于100 mm.ECC开裂面所能传递的最大剪应力也近似按式(13)和(14)计算,由于ECC中没有粗骨料,式中ag取为0.

(a) 裂缝间的平均拉应力

2 RECC梁受剪承载力计算方法

2.1 基于MCFT的RECC梁受剪承载力计算

将上述变形协调方程、平衡方程、材料本构关系和局部力平衡方程联立,通过Matlab编写了RECC梁的受剪承载力计算程序,主要计算过程如下:

① 输入RECC构件的基本参数,计算平均裂缝宽度ω,并预估主拉应变值ε1、斜压杆角度θ和箍筋中的应力fsy.

② 由式(7)、(5)、(6)分别计算f1,νxy和f2.

④ 由式(8)和(3)分别计算主压应变ε2和箍筋应变εy,计算箍筋的应力fsy=εyEs≤fsyy,fsyy为箍筋屈服强度,Es为钢筋弹性模量.

⑤ 验证fsy与第①步假设的fsy是否相等,如果不相等则重新假设新的fsy,从第②步开始重新迭代,如果相等,则进行下一步.

⑥ 由式(3)计算纵筋的应变值εx,计算纵筋的应力值fsx=εxEs≤fsxy,fsxy为纵筋屈服强度.

⑦ 计算RECC构件截面上承担的轴向力fx=f1-vxy/tanθ+ρsxfsx,式中,vxy=V/(bdv).

⑧ 验证fx是否等于RECC构件实际承受的轴力,对非预应力受弯构件,实际轴力为零,如果不满足重新选择θ,从第①步重新迭代,若满足则进行下一步.

⑨ Δf=f1-fcr1-ρsy(fsyy-fsy),如果Δf≤0,取骨料摩擦和咬合作用νci=0;裂缝处箍筋应力fscry和纵筋应力fscrx计算公式为

fscry=fsy+(f1-fcr1)/ρsy

(15)

fscrx=fsx+(f1-fcr1)/ρsx

(16)

如果Δf>0,

νci=Δf/tanθ

(17)

fscry=fsyy

(18)

(19)

验证fscrx≤fsxy或vci≤vci,max是否满足,如果不满足,重新选择ε1,并返回第①步继续迭代,若满足则为相应的最终结果.

RECC梁的受剪承载力无法通过上述计算程序一次性计算得出,通常需要经过几次试算来确保计算结果的准确性.试算时,可将2εy和4εy作为ε1的初始迭代值分别进行2次迭代运算,εy可取为箍筋屈服应变，对比2次计算得出的剪切荷载,若二者相等即为试件的受剪承载力,若不相等则需进一步增大ε1的初始迭代值(增幅建议为2εy)进行新的迭代计算,直至剪切荷载计算值与上一次试算结果相等为止.试件达到其受剪承载力时箍筋通常已经屈服,斜压杆角度θ一般在25°～45°之间变化,因此每次试算时fsy和斜压杆角度θ的初始迭代值可分别取为箍筋屈服强度和中间值35°.

2.2 拱模型

钢筋混凝土构件受剪承载力一般随剪跨比的减小而增大,对于钢筋混凝土梁,一般认为剪跨比小于2.5时[23]拱效应比较明显.MCFT理论是一种基于截面的抗剪设计方法,没有考虑拱效应,对剪跨比大于2.5构件的受剪承载力预测较为准确.因此,对于剪跨比大于2.5的RECC梁,其受剪承载力直接使用本文提出的修正MCFT模型计算;对于剪跨比小于2.5的梁,本文将采用桁架-拱模型预测其受剪承载力V[24],即V=Vt+Va.桁架模型对受剪承载力的贡献项Vt按修正MCFT理论进行计算,而拱模型则可简化为一根自构件顶部受压区至底部受压区的斜压杆,如图4所示.拱效应所提供的抗剪强度Va可按下式计算:

(20)

(21)

(22)

图4 拱模型的基本受力单元

ECC的压应力为拱模型和桁架模型中ECC压应力的叠加,但是桁架机构中ECC斜压杆与拱杆的角度不同,这里简单地认为斜压杆总压应力为二者的相加.

2.3 RECC梁剪切试验数据库

2.4 修正MCFT计算结果与试验结果的对比

由修正MCFT理论得到的受剪承载力Vpre与剪切数据库中RECC梁的实测受剪承载力Vexp的对比情况如图5所示.图中数据点较为紧密地分布在对角线附近,试验强度与计算强度的比值RS的均值及变异系数分别为0.976和0.199,说明本文提出的修正MCFT理论可较为准确地预测RECC梁的受剪承载力.结合拱模型,修正MCFT理论也能够适用于剪跨比小于2.5的RECC梁.

图5 基于修正MCFT的受剪承载力计算值与试验值的比较

3 有腹筋RECC梁受剪承载力简化计算公式

尽管本文提出的修正MCFT理论能够合理地预测RECC梁的受剪承载力,但是该计算模型仍存在2个问题:① MCFT理论用于常规设计过于复杂,精确计算需要一定的迭代过程;② 相对延性较大的弯曲破坏模式,剪切破坏在设计中应予以避免. 因此,如果一个抗剪设计方法得到的RS数学期望接近1,并不表示该方法较优,从设计角度而言,RS应该略大于1,以保证足够的安全性.文献[27]基于MCFT理论,推导了混凝土斜压杆角度的显式计算公式,提出了有腹筋钢筋混凝土梁受剪承载力的简化计算公式,并得到了较高的计算精度.因此,本文拟采用文献[27]中提出的简化方法,推导RECC梁的受剪承载力简化计算公式.

3.1 ECC对抗剪的贡献项VECC

如图3所示,本文提出的修正MCFT考虑了裂缝间及裂缝处ECC拉应力对抗剪的贡献项.因此,ECC对抗剪的贡献VECC可取开裂ECC主拉应力传递剪力的能力V1和通过开裂面骨料咬合作用及纤维桥接作用传递剪力的能力V2之间的较小值.依据图3中力平衡关系,V1和V2可表示为

V1=(90ε1+1)fcrbdvcotθ

(23)

(24)

因此,ECC对抗剪的贡献项VECC为min(V1,V2).另外,箍筋对抗剪的贡献项Vs可表示为

(25)

从式(23)和(24)中可看出,ECC对抗剪的贡献中有2个未知数,即斜压杆角度θ及斜向开裂ECC的主拉应变ε1.为了得到显式的受剪承载力计算公式,需推导出θ和ε1的简化计算公式.

3.2 斜压杆角度θ计算公式推导

文献[27]在计算钢筋混凝土梁受剪承载力时,假定箍筋进入屈服为斜截面破坏的标识,此时剪力一般稍小于剪压区压溃时的剪力,采用箍筋屈服这一标识,设计相对安全,但不失准确性.本文在计算ECC斜压杆角度θ时,同样沿用该假定.临近箍筋屈服时,箍筋、纵筋及ECC斜压杆一般均可假定处在线性阶段,即fsy=nEcεy,fsx=nEcεx,ε2=f2/Ec,n=Es/Ec;此外,由式(10)和(11)可知,f1=vECCtanθ,其中vECC=VECC/(bdv),代入到式(4)～(6)中,联合变形协调条件式(3),可得

tan2θ=

(26)

由于式(26)中包含了未知的vECC和vxy,使得求解θ需要经过繁琐的迭代,现对式(26)进行合理的简化.在利用修正MCFT理论计算数据库中RECC梁的受剪承载力过程中,作者发现受剪破坏时,vECC/vxy一般在30%～80%之间变化.将不同的vECC/vxy代入式(26),可得到一个一元四次方程,经过简单的迭代可得到θ,其计算结果如图6所示,图中n取为10.从图中可看出,vECC/vxy对θ的计算值影响较小,这里假定vECC/vxy取数据库计算结果的均值0.55,式(26)可简化为

(27)

图6 不同vECC/vxy对斜压杆角度θ的影响

对式(27)进行试算发现,式(27)右边项的θ取值对式(27)最终值的影响不大.剪切数据库计算结果表明,斜压杆角度θ一般在25°～45°之间变化,因此可将式(27)右边项的θ取为中间值35°,则式(27)可进一步简化为

(28)

图7比较了式(27)与简化式(28)计算值差异

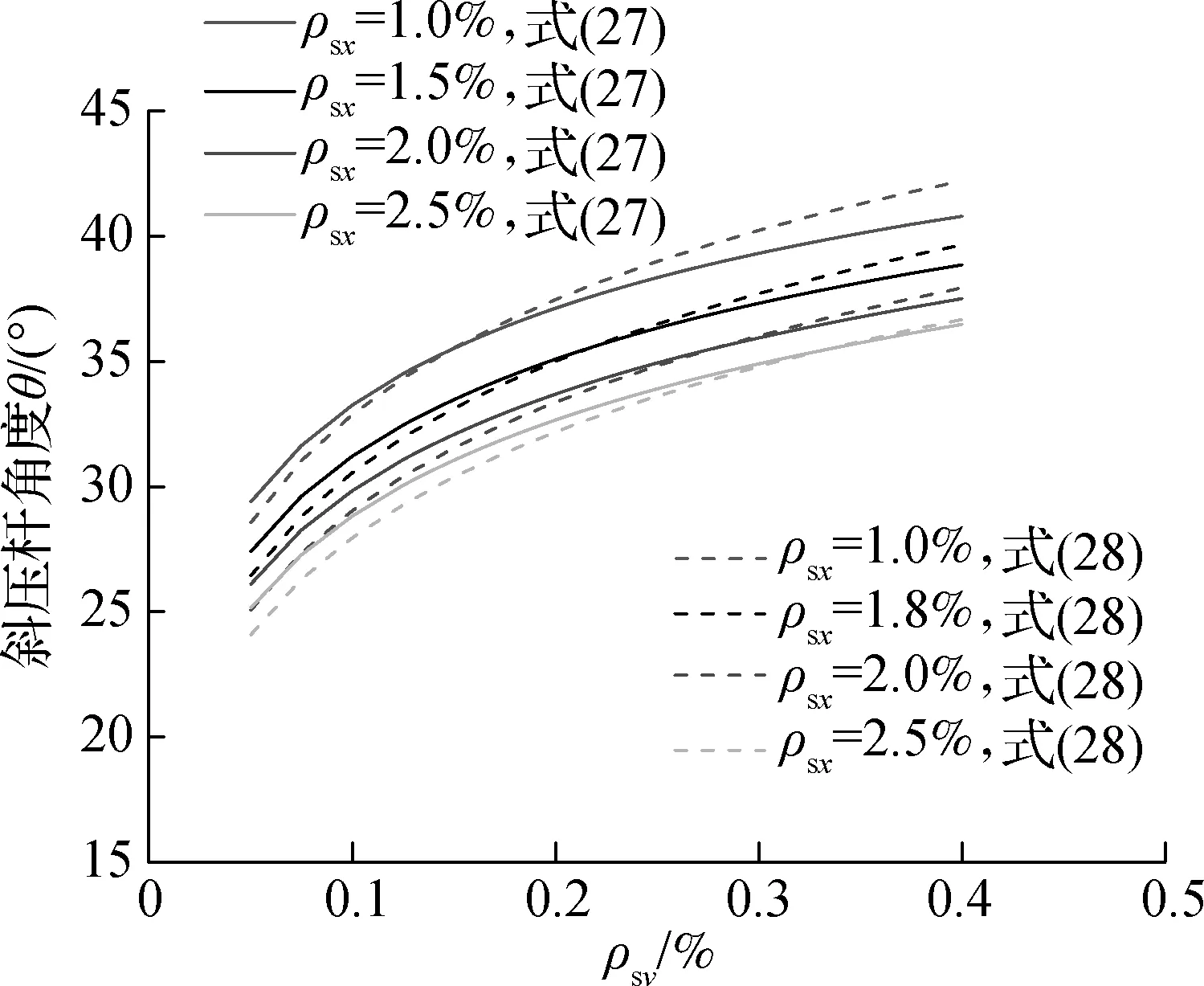
图7 简化式(28)与式(27)计算值差异比较

(n=10).由图7可见,两者计算值差异非常小.

3.3 ECC平均主拉应变ε1的简化计算方法

文献[28]基于箍筋应变εy建立了混凝土构件斜裂缝宽度的计算方法,而直接影响斜裂缝宽度的是开裂混凝土的平均主拉应变ε1,即ε1和箍筋应变εy存在某种联系[27].本文直接将ε1与箍筋刚屈服时的εy联系起来,通过对数据库中有腹筋钢筋混凝土梁受剪承载力的计算,回归分析得出ε1=1.35εy.鉴于此,本文针对数据库中的29根有腹筋RECC梁,利用已提出的修正MCFT理论，分析了箍筋屈服时ε1与εy的关系,得到ε1/εy均值为1.75,将ε1=1.75εy和式(28)代入式(23)～(25),可计算出ECC构件受剪承载力为

V=VECC+Vs

(29)

其中

(30)

3.4 简化计算结果与试验结果的对比

为验证简化计算方法的准确性,提取数据库中29根有腹筋RECC梁,对其受剪承载力试验结果进行验算.其中,剪跨比大于2.5的梁,其受剪承载力直接由简化方法计算得出;剪跨比小于2.5的梁,由上述桁架-拱模型得出,其中桁架模型采用简化方法计算,拱模型由式(20)和(21)计算得出.图8显示了简化方法计算得到的RECC梁受剪承载力Vspre与实测受剪承载力Vexp的对比情况.如图8所示,试验强度与计算强度的比值RS的均值及变异系数分别为1.05和0.197.可见简化方法的计算值与试验值吻合较好,且预测值比实测值稍小,在保证抗剪设计安全性的前提下,简化方法还给出了显式的计算公式,与修正MCFT理论相比,更适合于RECC梁抗剪常规设计.

图8 简化计算方法得到的受剪承载力计算值与数据库试验值的比较

4 结论

1) 本文基于修正压力场理论,并根据ECC的特性,对ECC主应力-主应变关系和局部应力平衡方程进行了修正,考虑了裂缝间和裂缝处纤维的桥接作用对抗剪的有利作用,提出了适用于RECC梁的修正MCFT理论.

2) 建立了40个RECC梁和6个RECC板的剪切试验数据库,验证本文提出的修正MCFT理论的合理性,计算结果表明,修正MCFT方法具有较好的计算精度,适用于RECC梁受剪承载力计算.

3) 基于修正MCFT理论进行合理简化,推导了ECC斜压杆角度的显式计算公式.将斜裂缝间ECC主拉应变与箍筋刚屈服时的应变联系起来,得到有腹筋ECC构件受剪承载力的简化计算公式,相比修正MCFT理论,无需繁琐的迭代计算.采用简化计算公式预测剪切数据库中29根有腹筋RECC梁的受剪承载力,试验值与计算值比值的均值和变异系数分别为1.05和0.197,预测精度较高.