控制量权重可变的主动段最优中制导律*

马自茹，魏明英，李运迁

(1.北京电子工程总体研究所，北京 100854；2.中国航天科工集团有限公司 第二研究院，北京 100854；3.空天防御创新中心，北京 100854)

0 引言

现代战争中，弹道导弹无疑是威胁最大的一种武器，所以对弹道导弹的高精度拦截就显得尤为重要。弹道导弹的飞行一般分为3个阶段，主动段，中段和末段。主动段拦截，从拦截效果上来看是最理想的，但是需要克服的困难也很多，需要的外界条件很难达到，所以现代的防空导弹，都以中段或末段拦截为目标。无论是中段拦截还是末段拦截，都普遍采用复合制导的方式，整个制导过程分为初制导，中制导和末制导。其中，中制导需要达到的制导目标是最复杂的，需要满足的约束是最多样化的。

一般来说，末制导的初始条件就是中制导的制导目标[1]。为了保证中末制导可靠地交班，保证最终命中目标，对中制导段提出3方面的要求：①控制导引头测量轴指向目标，其控制误差不应超出弹上测量装置的视场范围；②导弹与目标的距离应在导引头的测量范围之内；③导弹的速度应满足末制导的初始要求。除此之外，在实际中，对于中制导还有着很多其他的要求。首先，现在的防空导弹，多是主动飞行与被动飞行相结合，并且使用拦截器直接碰撞的拦截方式，这就要求导弹在飞行的过程中保留足够的动能，要求控制能量尽可能小。此外，对于一些静不稳定度比较大的导弹，当攻角比较大，过载比较大的时候，容易使姿态彻底失控，所以对于这类导弹，要求整个飞行过程中的过载尽可能的小。传统中制导常采用比例导引的方法，这种方法在制导精度上可以满足要求，但是无法引入更多的约束，其过载曲线往往峰值较大，变化剧烈，相应的，控制能量损失也很大。

目前，很多中外论文都将最优控制理论应用于中制导律的解算当中。文献[2]基于E-Guidance理论[3]，给出了一种最优制导律，实现将导弹从初始状态控制到预测的末位置，满足最终速度倾角约束，同时满足使导弹速度最大的优化目的。但是这种方法得到的结果，形式复杂，而且很难直接应用到实际的仿真程序中。文献[4-5]采用最速上升法求解2点边值问题，但是直接求解2点边值问题计算量大，难以在弹上实时完成，文献[5]设计了一种带角度约束的制导律，但是并没有考虑导弹速度的变化率，对于主动段飞行的导弹来说，速度变化率是不可忽略的一个因素。文献[6]所要解决的问题与本文是类似的，同样是在中制导末端满足速度的角度约束，但是对于控制量的约束，仅仅限于在指标函数中使控制能量最小，而没有做更多的改进，在仿真验证中，这种导引律的实际过载在飞行前期较大。文献[7-14]虽然研究对象不同，但是在解算方法上都是类似的，但是在建立的指标函数中，控制量的权重依然是1或者常数，这就使得在解算出控制量算法后，无法再对控制量的大小进行调整。文献[15]给出了一种使用时变控制量权重的高斯伪谱法，说明时变的控制量权重的可行性。

本文研究的问题是，在导弹飞行的主动段，考虑导弹速度变化率，将导弹控制到预测点，使末位置误差尽可能小，同时满足末速度倾角约束，满足视线角变化率趋向于0，并且导弹过载更小。为了满足以上约束，本文将所有约束条件统筹到一个指标函数当中，通过极小值原理解算控制量的解析形式。为了使飞行中的过载更有可控性，变化更平缓，整体更小，采用在指标函数中加入可变控制量权重的办法，这种方法得到的制导律，可以通过调节控制量计算式中的参数来实现对不同阶段过载大小的控制。分别给出了离散式和解析式算法的推导过程。

1 导弹运动模型

建立导弹的运动模型。将导弹的运动分解为横向和纵向，先研究纵向平面的运动，如图1所示。图1的坐标系，是以导弹和目标点连线所在的平面为坐标系的Oxy平面，而在实际的仿真模型中，这个坐标系不是标准坐标系之一，所以要进行坐标变换。图1中，M0为导弹的初始位置;Mf为导弹的飞行目标点;v0为导弹的初速度;vf为导弹的末速度;θ0为导弹的初始速度倾角;θf为导弹的末状态速度倾角，也是控制目标;q为导弹到目标点的视线角;R为相对距离。则，在纵向平面内，导弹飞向目标点的运动模型为

(1)

2 最优制导律

2.1 状态方程和指标函数的建立与解算

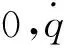
θ(t)=q(t),

(2)

所以，在末位置时，如果满足

q(t)-θ(tf)=0,

(3)

则同时满足

θ(t)-θ(tf)=0.

(4)

(5)

是一种很理想的交班情况。

对于一个最优控制问题，建立状态方程是很关键的步骤，需要把约束条件涉及的变量设为状态变量，决定了使用最优理论解算的目标，同时也决定了解算过程的繁复程度以及是否能够得到解析解。有一些简单的状态方程类型是可以得到解析解的，双积分系统就是其中之一，这里在建立状态方程时，建成了双积分系统的形式。

对式(1)中间等式求导运算：

(6)

式(6)结合式(1)可得

(7)

根据之前叙述的约束条件，取状态量为式(8)形式

(8)

则有系统状态方程式

(9)

根据前文分析，为了在接下来的解算中，更容易得到解析解，这里通过引入伪控制量的办法，将系统形式写成双积分系统。令

(10)

则有新系统

(11)

考虑约束条件，列写指标函数。这里要考虑的约束有，系统2个状态变量的末状态，控制量尽可能地小。所以有指标函数式

(12)

直接将控制能量的比重r阵取为1。而c1，c2的取值由末状态约束决定。

对于这种双积分系统，针对式(12)形式的指标函数，利用极小值原理可以得到解析解，这个过程已经为人们熟知[6]，这里不做详细介绍，直接给出结果。

(13)

约束要求，x1(tf)=0，x2(tf)=0，则c1和c2→∞，则式(13)可转化为

(14)

(15)

2.2 最优导引律的改进，可变权系数的指标方程解算

一般的二次型指标函数形式为

(16)

u(t)=-r-1(t)BT(t)K(t)X(t),

(17)

式中：r与u(t)为求逆关系。总之，当r取比较大的值时，也就是说，控制量在指标函数中所占比重较大，而求解的目标是使指标函数取极小，则控制量的值会比较小。

使用最优导引律的弹道，前期过载大，变化剧烈，后期过载小，变化平缓，希望能对其改进，实现前期和后期的一种平衡，对前期进行抑制，而后期则进行放大。这就要求改变r的形式，使前期控制量在指标函数中的比重较大，后期在指标函数中的比重较小。设新的指标函数为

(18)

这里r由常数阵改成了时变阵，已经不适合于上文中给出过的解的形式，需要另行推导。有2种方法可以解决这个问题，一个是离散的方法，另一个是根据极小值原理直接推导。前者推导容易实现，但是在应用中要求的计算量大，后者推导难度大，但是在应用中要求的计算量较小。

下面给出，针对系统(11)和指标函数式(18)，利用极小值原理的解析解解算过程。将式(16)写成

(19)

根据式(19)和系统方程，汉密尔顿方程为

(20)

根据极小值原理，写出橫截条件，终值条件和控制方程

(21)

观察控制量的形式，发现欲求控制量，必须先求λ2。这里有的是，λ2的一阶导数和末值，理论上肯定可以求解，直接解算的结果中会包含x1(tf)，x2(tf)2个量。

(22)

式(22)可得

λ2(t)=λ2(tf)+c1tg(t)x1(tf)=

c2x2(tf)+c1tgx1(tf),

(23)

代入控制量的表达式

u(t)=-tg(t)-nc2x2(tf)-tg(t)-n+1c1x1(tf).

(24)

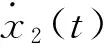
(25)

由式(25)可算得

(26)

因为

(27)

所以积分可得

(28)

根据式(27)和(28)可以解算x1(tf)，x2(tf)，如果直接解算，由于每项的系数很复杂，容易出错，这里将其设为

(29)

根据式(27)，(28)，(29)可以计算得到

(30)

前文叙述，约束要求2个状态末值为0，所以取c1和c2→∞。将式(30)代入式(24)可得

(31)

因为在建立指标函数的时候，用的是r(t)=tg(t)n，这样虽然解算过程稍微复杂一些，但是却具有普适性，n的取值不同，可以达到不同的优化目的。当n>0的时候，前期控制量在指标函数中的比重大，后期小，这样可以实现使前期过载较小，后期过载较大的优化目的，而当n<0时正相反，可以实现前期过载较大，迅速缩小与控制目标的偏差，而后期则过载较小，这也是具有应用意义的，比如，对于一些直接针对目标的制导问题，越到飞行后期，需要过载的大小对目标的机动的反映就越明显，所以希望在飞行前期尽快缩小偏差，而后期的过载尽可能小。

3 仿真验证

仿真程序考虑全弹气动力、万有引力、发动机推力、控制系统包含、制导部分、控制部分、导航部分。其中，本文推导的制导律主要编入制导部分。在导航基准坐标系中，初制导结束时，即主动段中制导开始时的状态为已知，即位置，速度，弹道倾角和弹道偏角皆已知，控制目标为，预测点xf，yf，zf，以及弹道倾角和弹道偏角的期望值。

主要针对弹道倾角，即纵向进行制导控制。注意，在前文中建立的导弹运动模型，是将导弹的纵向运动平面放置在Oxy平面内，这种坐标系并不是常用的几种坐标系定义，所以需要在导航坐标系的基础上进行坐标系变换，将导航基准坐标系的Oxy面转到导弹纵向运动的平面内，即绕y轴转一个弹道偏角即可。

分别针对原有制导律(theoriginal)，最优制导律(qtheta)和可变权系数制导律进行仿真验证。主要关心的数据为，弹道倾角终值与目标值的差，导弹y向过载大小，弹目视线角变化率的归零快慢，位置误差。

3.1 弹道倾角变化

将原有制导律，最优制导律和可变权系数制导律的2种情况的弹道倾角变化曲线绘制在图2中，根据曲线可以发现，原有制导律的快速性较差。而当n取正值或者负值时，可变权系数制导律的曲线分别在最优制导律的上侧和下侧，这也印证了前文的理论推测。

几种制导律的弹道倾角末值与期望值的偏差如表1所示，单位为rad。

表1 制导律的弹道倾角末值与期望Table 1 Trajectory inclination terminal value and expectation of guidance law rad

可以发现，最优导引律的精度最佳，其误差在0.004以内。

3.2 过载变化

将这些导引律的过载变化曲线分成2组进行对比，第1组对比theoriginal和qtheta，意在分析最优方法解算出导引律与其他方法的不同，第2组为包含qtheta和可变权系数导引律，这是对最优导引律的改进，意在表现改进的效果。

第1组如图3所示，发现原本的导引律，过载峰值大，变化剧烈，而且后期存在连续抖动，对于一些静不稳定度大的导弹，这种过载曲线是很不理想的。以最优理论推导出的导引律，如前面所预测的那样，前期峰值大，变化剧烈，但是后期较小且变化平稳，这种导引律是精度最高的。

第2组如图4所示，这一组主要是用来分析对最优导引律的改进效果，其他曲线都与qtheta进行对比分析。可变权系数的方法推得的导引律是比较理想的，这里分别取n=1和n=-1，试验证明，当n=1时，前期的过载得到了抑制，后期由于在程序里使用限幅模块，即当精度达到要求之后，就领导引律计算结果为0，所以在这里体现的并不明显。n=-1的导引律在前期过载较大，变化剧烈，但是从图1中可以看出，这样的大过载增加了快速性，使倾角很快的就达到了目标值附近。但是付出一倍多的过载增大是不值得的。

4 结束语

本文针对复合制导中的主动段中制导，将导弹导引至目标点并满足角度约束的问题，考虑导弹的速度变化率，建立了导弹的运动模型。根据给出的约束条件选择状态变量建立了系统状态方程。使用最优理论推导了导引律，仿真试验证明，使用最优理论的导引律精度最高，过载大小和变化的剧烈程度均优于原有导引律，而且在推导过程中加入的约束都满足。试验证明，最优理论是解决多约束中制导问题的有力工具。

而后对最优导引律提出了改进方案，可变权系数法，需要重新用极小值原理推导算法，给出了离散法和解析法2个结果。仿真试验证明，可变权系数的方法达到了预期的效果，当n取不同值时，其对控制量有不同的限制，这种方法和思路在其他中制导过程和末制导中也会有很大的发展空间，本文证明了这种想法的正确性。