地月空间DRO与HEO(3∶1/2∶1)共振轨道延拓求解及其稳定性分析

彭 超，温昶煊，高 扬

(1. 中国科学院空间应用工程与技术中心，北京 100094； 2. 中科院太空应用重点实验室，北京 100094； 3. 中国科学院大学，北京 100094)

1 引言

地月系统是一个典型的圆形限制性三体系统，圆形限制性三体问题目前还没有像开普勒轨道那样的解析解，研究主要依赖于数值方法。基于动力系统理论的圆形限制性三体问题的平衡点与周期轨道是最早被关注的问题[1-3]。平衡点即为拉格朗日点，即圆形限制性三体问题中的L1-L5点，已牵引出一系列拉格朗日点空间任务[4-6]；与此同时，地月系统圆形限制性三体问题中周期轨道的分析与应用研究也早已开展[7-8]，其中轨道周期与月球公转周期接近简单整数比的周期轨道被称为相对月球的共振轨道[9]。

共振轨道(或轨道共振)的概念最早源于天体力学研究[10]。它在自然界普遍存在，在行星系中的卫星轨道、恒星系中的行星轨道均能够找到相应现象[9]。木卫1、木卫2与木卫3围绕木星的公转轨道周期呈现 4∶2∶1的比例关系，该现象称为拉普拉斯共振(Laplace Resonance)[11]；土星、天王星、海王星等其它类木星行星系中的卫星轨道同样存在类似的轨道共振现象[9-11]；在太阳系中，分布在太阳-木星组成的三体系统拉格朗日点L4、L5附近的特洛伊带小行星与木星呈现稳定的1∶1轨道共振现象，并处于长期稳定运行状态[12]；主带小行星轨道(半长轴分布在2AU-3AU)空间分布的柯克伍德缝隙(Kirkwood Gap)也源于共振轨道原理，由于与木星呈现3∶1、5∶2、7∶3比例关系的共振轨道的不稳定性，可以清晰地发现主带小行星半长轴在2.5AU、2.82AU、2.95AU(分别对应3∶1、5∶2、7∶3共振比)处不再出现[13]。

基于天体共振轨道的基本原理，学者们设计了航天器共振轨道，并已经广泛运用到多次引力辅助任务设计中，还在最近的任务中充当了长期稳定的轨道。比如在NASA的外层行星计划中(Outer Planets Program)，木卫二轨道飞行器在最后阶段利用共振轨道连续两次飞跃木卫二，最后进入木卫二轨道[14-16]。发射于2008年的IBEX(Interstellar Boundary Explorer)航天器进入地球高轨，但归因于月球引力摄动的影响，任务轨道无法长周期预报；2011年，IBEX航天器转移到一条与月球公转周期成3∶1的稳定共振轨道上，现在这颗卫星消耗更少的燃料就能维持在稳定轨道，使它的工作年限增加到40多年[17-18]。IBEX航天器轨道的成功启发人们将共振轨道用作其他方面的空间任务。NASA于2013年宣布的太阳系外行星观测任务(Transiting Exoplanet Survey Satellite，于2018年4月发射)中，观测卫星直接进入到长期稳定的月球共振轨道以便长期观测行星[19]。由此可见，共振轨道有着巨大的应用潜力，深刻理解共振轨道的动力学特征对空间任务设计有着重要意义。

在地月旋转坐标系下，共振轨道包含环绕月球与环绕地球的两类。本文首先关注地月空间远距逆向轨道(Distant Retrograde Orbit，DRO)，它属于环绕月球的共振轨道。在地月旋转坐标系下，DRO逆行环绕月球做周期运动。NASA的小行星重定向任务曾计划将一颗近地小行星捕获到DRO[20-21]。由于DRO可长期保持稳定，放置在DRO的近地小行星能在该轨道维持数百年之久[21-22]，并且小行星能从深空低能量捕获进入DRO[23]。日地系统DRO相关研究出现更早，Ocampo与Rosborough提出利用日地系统DRO部署天基望远镜的应用设想[24]，Demeyer与Gurl[25]以及Scott与Spencer[26]分别为此研究了转移到日地系DRO的轨道设计方法。徐明与徐世杰提出了地月系DRO作为中继通信的设想，并研究了转移轨道设计方法[27]。Conte等对于地火转移采用DRO作为中转站开展了研究[28]。本文同时关注另一类环绕地球的大偏心率共振轨道族(Highly Eccentric Orbit，HEO，3∶1与2∶1共振)。与载人登月所利用的自由往返轨道类似(接近5∶2共振)[29]，HEO同样可形成自由往返轨道，并可实现地球高轨与月球附近的自由往返，且HEO(2∶1)可形成拱线进动的太阳同步状态，有利于对地球磁层与太阳风相互作用的观测。与DRO相比，HEO(3∶1)与(2∶1)一般都不稳定，需要进行轨道维持[30]。梁等计算了地月空间的多边形周期轨道(Polygonal-Like Periodic Orbit，PLPO，包含HEO(3∶1))，并提出采用霍曼转移实现入轨的方案[36]。

本文针对共振轨道的动力学特征，分别从地球与月球附近延拓求解相应的周期轨道，并分析地月系统圆形限制性三体模型下月球公转轨道面内DRO与HEO两类共振轨道族及其稳定性。从远离月球或地球的二体模型中开普勒共振轨道(月球公转周期与轨道周期符合1∶1、2∶1与3∶1的比例关系)得到圆形限制性三体模型中的两类周期轨道初值，然后通过延拓“近地点距”得到可接近月球或地球的圆形限制性三体周期轨道族。同时描述DRO的非开普勒特征与共振特性，澄清不同模型共振轨道的概念，利用轨道周期的变化描述相同共振比对应不同共振轨道的现象，并利用动力系统理论对这两类周期轨道进行稳定性分析，基于HEO(2∶1)描述拱线进动太阳同步轨道概念，并以HEO(3∶1)共振轨道为例估算长期维持所需的速度增量。

2 基本分析模型

圆形限制性三体问题是本文分析共振轨道的基本模型。它是N体问题的一个特例，假设惯性空间中只有m1、m2、m3，并且m3的质量远远小于m1和m2，m1和m2的运动不受m3的影响。因此，m1和m2满足二体问题的结论，即m1和m2围绕它们共同的质心做圆周运动，m1和m2的共同质心在惯性空间中静止和匀速直线运动[4]。如果我们将m3看作人造航天器，m1和m2是两个天体，例如地球和月球，就得到了地月系统圆形限制性三体问题。该问题可以在如图1所示的惯性空间中的一个旋转坐标系中研究，坐标系的原点位于两个天体的共同质心，m1和m2围绕它们共同的质心做圆周运动，其中m1是较大的天体，m2是较小的天体，m3是航天器S/C。

图1 圆形限制性三体问题示意图Fig.1 The circular restricted three-body problem

图1中，较大天体m1到质心(坐标原点)的距离为D1，较小天体m2到质心的距离为D2，m1到S/C的距离为r1，m2到S/C的距离为r2。设距离单位为D(D=D1+D2)，时间单位为1/n(n为小天体围绕大天体运动的角速度)，那么航天器S/C在旋转坐标系中的无量纲动力学方程如式(1)：

(1)

式(1)所示圆形限制性三体动力学方程存在着对称性，即由一条标准轨道可映射出两种镜像轨道[31]：①与平面对称的镜像轨道；②与轴对称的镜像轨道。与平面对称的镜像轨道是将标准轨道以该平面为对称面映射出的一条轨道，该镜像轨道与标准轨道在垂直于对称面的分量互为相反数。与轴对称的镜像轨道是将标准轨道以该轴为旋转轴，旋转180°而获得的一条轨道，该映射轨道在垂直于旋转轴上的分量与标准轨道互为相反数。圆形限制性三体的对称性可由动力学方程(1)证明[31]。因此，圆形限制性三体中的对称性预示着该模型下存在着两类对称周期轨道：①关于X-Z平面对称的周期轨道；②关于X轴对称的周期轨道。利用牛顿微分迭代可求解这两类周期轨道。

3 DRO与HEO(2∶1/3∶1)共振轨道延拓求解

定义二体模型下顺行绕地的开普勒共振轨道的共振比p·q为：月球公转轨道周期与航天器轨道周期的整数比例关系。共振比还可以理解为：航天器绕地球旋转p圈的时间段内，月球绕地球旋转q圈。我们将此类共振轨道称为“地心系开普勒共振轨道”。考虑共振轨道关于X轴对称，在Y=0时航天器速度垂直于地月连线且在地月公转平面内。这种对称的地心系开普勒共振轨道的主要设计参数为共振比p·q与近地点地心距x0，当这两个参数给定，那么可以唯一确定一条共振轨道，其近地点或远地点在某一参考时刻的地月连线上。

图2 初值在地球附近的1∶1共振轨道(左图为地月旋转系，右图为地心惯性系)Fig.2 The 1∶1 resonant orbit near the Earth (the left picture was plotted in the rotating frame, the right picture was plotted in inertial frame)

图3 初值在月球附近的周期轨道(左图为地月旋转系，右图为地心惯性系)Fig.3 The periodic orbit near the Moon (the left picture was plotted in the rotating frame, the right picture was plotted in inertial frame)

图3显示1∶1共振轨道延拓到三体模型下成为环月轨道。由于月球引力的影响，周期从原来的一个月球周期(2π)变成了0.021936(可认为环月轨道周期)，轨道形状发生了大幅改变。右图中的黑色轨道为一个轨道周期的轨迹，当多个周期后，航天器会再次回到x0附近，如蓝色轨道显示。

在得到图2～3所示的圆形限制性三体共振轨道之后，延拓x0(逐步增大或减少)以获得DRO周期轨道族。周期轨道的迭代初值都由相邻的已迭代出的限制性三体共振轨道给出。当周期轨道距离月球或地球300 km，或无法延拓时(延拓迭代无法收敛)，延拓过程终止，所得到的两类周期轨道族初始位置x0与速度vy(Y轴方向速度)的关系如图4：

图4 DRO周期轨道族的位置x0与速度关系Fig.4 The velocities of the family of DRO as a function of the DRO’s x0 values

图4显示两类周期轨道族的曲线一致，说明它们是同一个轨道族。所得到的DRO周期轨道族如图5所示，图5中的箭头方向代表轨道运动方向。

图6 初值在地球附近的HEO(2∶1)共振轨道(左图为地月旋转系，右图为地心惯性系)Fig.6 The HEO (2∶1) near the Earth (the left picture was plotted in the rotating frame, the right picture was plotted in inertial frame)

图5 DRO轨道周期轨道族(地月旋转系)Fig.5 The family of DRO (plotted in the rotating frame)

图7 初值在月球附近的HEO(2∶1)共振轨道(左图为地月旋转系，右图为地心惯性系)Fig.7 The HEO (2∶1) near the Moon (the left picture was plotted in the rotating frame, the right picture was plotted in inertial frame)

得到图6～7所示的圆形限制性三体共振轨道之后，延拓x0(逐步增大或减少)以获得周期轨道族。当周期轨道距离天体300 km或无法继续延拓时，延拓过程终止，所得到的两类周期轨道族初始位置与速度曲线如图8。

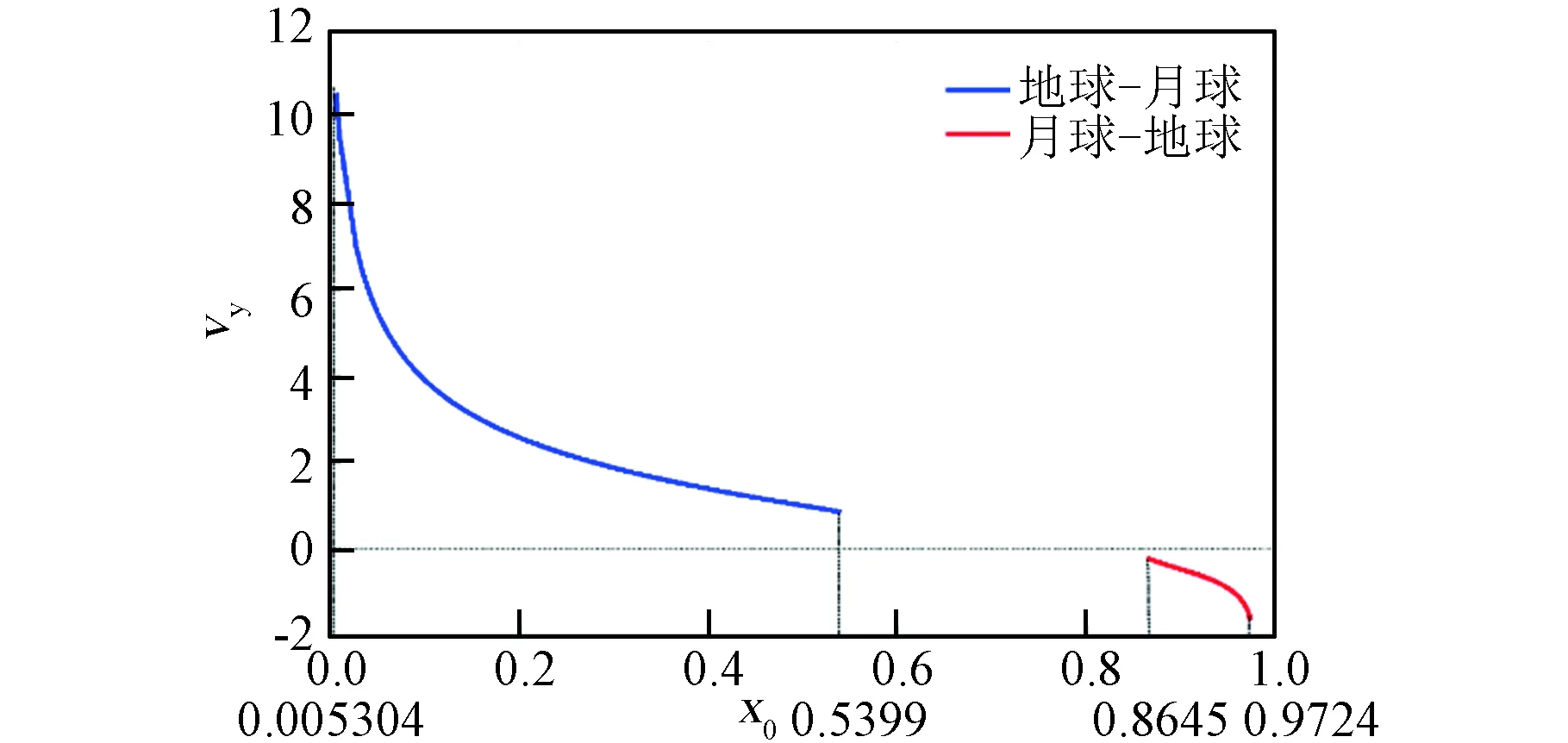
图8 HEO(2∶1)共振轨道族的位置x0与速度关系Fig.8 The velocities of the family of HEO (2∶1) as a function of the x0 values

图9 图6轨道延拓的HEO(2∶1)共振周期轨道族(左图为地月旋转系，右图为地心惯性系)Fig.9 The family of HEO (2∶1) continued from the orbit in figure 6 (the left picture was plotted in the rotating frame, the right picture was plotted in inertial frame)

从图8可知：图6的共振轨道只能延拓到x0=0.5399处(蓝色曲线)；图7的共振轨道只能延拓到x0=0.8645处(红色曲线)。它们分别属于不同的轨道族，其中初始位置x0在[0.005304 0.5399]区间的轨道族的初始速度vy大于0，而在[0.8645 0.9724]区间的初始速度vy小于0。

图6与图7中的2∶1共振轨道族分别如图9与图10所示。

采取相同的延拓方法(延拓x0)，得到的两类周期轨道族初始位置速度曲线如图13。

显然它们属于不同的轨道族，图11轨道只能延拓到x0=0.5399处；图12轨道则可延拓到地球附近。从月球到地球方向延拓的过程中(红色曲线)，在x0=0.7544处速度vy=0，意味着在此处速度方向发生变化。两条曲线相切于A点，即在A点处两类共振轨道是同一条轨道。在A点向月球延拓会沿着蓝色曲线从而最后终止于x0=0.5399，而向地球延拓则沿着红色曲线最终到达地球附近。两类周期轨道族如图14～15所示。其中图15说明从月球附近向地球附近延拓过程中，3∶1共振轨道会逐渐形成绕地轨道，尤其当轨道远离月球，受到月球引力比较小时，可视为地心系开普勒轨道。

图10 图7轨道延拓的HEO(2∶1)共振周期轨道族(左图为地月旋转系，右图为地心惯性系)Fig.10 The family of HEO (2∶1) continued from the orbit in figure 7 (the left picture was plotted in the rotating frame, the right picture was plotted in inertial frame)

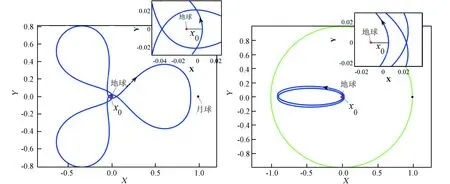
图11 初值在地球附近的HEO(3∶1)共振轨道(左图为地月旋转系，右图为地心惯性系)Fig.11 The HEO (3∶1) near the Earth (the left picture was plotted in the rotating frame, the right picture was plotted in inertial frame)

图12 初值在月球附近的HEO(3∶1)共振轨道(左图为地月旋转系，右图为地心惯性系)Fig.12 The HEO (3∶1) near the Moon (the left picture was plotted in the rotating frame, the right picture was plotted in inertial frame)

图13 两类HEO(3∶1)周期轨道族的位置x0与速度关系Fig.13 The velocities of the family of HEO (3∶1) as a function of the x0 values

由图5、图14与图15可知：当1∶1共振轨道延拓到月球附近，会逐渐变成逆行绕月轨道(Distant Retrograde Orbit，DRO)；形如三叶草的3∶1共振轨道在接近月球的情况下，靠近月球一侧的形状会明显偏大，而从月球延拓到地球附近时，会逐渐变成一条绕地轨道。说明月球引力会影响到共振轨道的形状与周期。

在圆形限制性三体模型下的闭合共振轨道在地心惯性系中不再闭合。只有整数比的共振轨道既在地月旋转系下闭合，又在地心惯性系下闭合。圆形限制性三体共振轨道周期无法像开普勒轨道那样计算(即仅与半长轴相关)。我们需要重新审视圆形限制性三体中的共振比概念，但共振比仍可定义为月球公转轨道周期与绕地轨道周期比例关系，共振比接近整数比的轨道仍然被称为共振轨道。

图14 图11轨道延拓的HEO(3∶1)共振周期轨道族(左图为地月旋转系，右图为地心惯性系)Fig.14 The family of HEO (3∶1) continued from the orbit in figure 11 (the left picture was plotted in the rotating frame, the right picture was plotted in inertial frame)

图15 图12轨道延拓的HEO(3∶1)共振周期轨道族(左图为地月旋转系，右图为地心惯性系)Fig.15 The family of HEO (3∶1) continued from the orbit in figure 12 (the left picture was plotted in the rotating frame, the right picture was plotted in inertial frame)

图16显示了在地月旋转系与地心惯性系下的由1∶1开普勒共振轨道延拓所得的一条轨道。图中A为近地点，B为远地点。本文定义轨道周期为相邻两次经过近地点的时间。根据定义，航天器从A点出发经过B点再次回到A点为一个周期，在地月旋转坐标系下顺时针环月一周(如左图)，但在惯性系下环绕地球不到半圈(见右图)，原本1∶1共振比发生大的变化，变为接近2∶1。

图16 DRO共振轨道(左图为地月旋转系，右图为地心惯性系)Fig.16 The resonant orbit DRO (the left picture was plotted in the rotating frame, the right picture was plotted in inertial frame)

图17 HEO(3∶1)共振轨道(左图为地月旋转系，右图为地心惯性系)Fig.17 The resonant orbit HEO (3∶1) (the left picture was plotted in the rotating frame, the right picture was plotted in inertial frame)

图17为3∶1共振轨道族中的一条轨道，航天器从远地点B出发，依次经过近月点A1、A2与A3，在地月旋转坐标系下形成闭合的共振轨道。在圆形限制性三体模型下的一个轨道周期里，航天器在惯性系下环绕地球三圈，先后三次经过近地点与远地点，此时共振比变化并不大。因此根据文中周期定义，周期有三个时间段，分别是图中A1到A2的时间T1、A2到A3的时间T2与A3到A1的时间T3。由于三体模型下的对称性，T1=T2。而在月球引力的影响下，靠近月球的叶片要大于其他两个叶片，所以T3与T1、T2并不完全相等。因此，我们取周期T=(T1+T2+T3)/3，即三个周期的平均值。同理，2∶1共振轨道族中的周期计算与之类似，即为两个周期的平均值。

4 DRO非开普勒轨道特征与共振特性

当DRO初始位置在地球或月球附近时，轨道分别呈现地心或月心开普勒运动，比如图2与图3中的轨道。然而当DRO初始位置在地球与月球连线之间的某些位置时，会出现非开普勒特性。本文利用地心与月心惯性系下的能量E确定这一位置区间，其中E的表达式为式(2)：

(2)

其中下标c代表中心天体地球(earth)或月球(moon)，r与v为惯性系下航天器相对中心天体的位移与速度大小，GM为中心天体的引力常数。在圆形限制性三体模型下E不再是一个常量，而是有一定的波动。取每条DRO对应的最大能量Emax、最小能量Emin与平均能量Emax，如图18～19所示。

图18 DRO初始位置对应的地心惯性系最大能量Emax、平均能量Eaver与最小能量EminFig.18 The max energy Emax, average energy Eaver and min energy Emin of the family of DRO in ECI as a function of the x0 values

图19 DRO初始位置对应的月心惯性系最大能量Emax、平均能量Eaver与最小能量EminFig.19 The max energy Emax, average energy Eaver and min energy Emin of the family of DRO in LCI as a function of the x0 values

图20 地心惯性系下的HEO(2∶1/3∶1)共振周期轨道族初始位置对应的ErateFig.20 The Erate of the family of HEO (2∶1/3∶1) in ECI as a function of the x0 values

图18～19中DRO能量E波动得越大说明非开普勒特性越明显。从图中可知DRO初值在地球或月球附近时，能量E的波动幅值很小，可视为开普勒轨道。当DRO初值从地球附近向月球附近延拓时(或从月球附近向地球附近延拓)，波动的波动幅值越来越大，其非开普勒特性越来越明显。取参数Erate=(Emax-Emin)/|Eaver|×100%。本文定义：当轨道的Erate<25%时，则认为该轨道是开普勒轨道，或者是带摄动的开普勒轨道；当Erate>25%时，则认为该轨道是非开普勒轨道(定义旨在区分DRO与HEO的不同特性)。图18～19中的A与B点处的Erate=25%，因此，我们认为非开普勒的初始位置区间为x0∈[0.6856 0.8831]，即距离地心2.6×105km到3.4×105km之间。

同理，经延拓得到的HEO(2∶1/3∶1)周期共振轨道族(见图8与图13)依然可采用Erate确定其非开普勒特性。图20为2∶1与3∶1周期轨道族在地心惯性系下的Erate。Erate均不超过25%，说明它们是带摄动的地心开普勒轨道，不存在明显的非开普勒轨道特征。

DRO非开普勒特性包括其轨道族的周期变化。虽然DRO都是从1∶1共振轨道延拓而来，但是因为轨道周期的改变(周期变小)，可得到整数比2∶1、3∶1与4∶1的共振轨道，如图21所示，其中A点与B点之间为非开普勒区域。

这三种整数比共振轨道都在DRO的非开普勒区域内，由于是整数比的共振轨道，所以它们不仅在地月旋转系下是周期轨道(闭合)，在惯性系下也是周期轨道(闭合)，如图22～24所示。该三条DRO共振轨道从形状上也展现了明显的非开普勒轨道特征。DRO(2∶1)形状近似为椭圆形，但地球并不在焦点而在中心，在旋转系中逆行绕月2圈才能形成在惯性系中一条闭合轨道，分别2次经过近地点与远地点；DRO(3∶1/4∶1)形状无法近似为椭圆，非开普勒轨道特性更加明显，DRO(3∶1)分别3次经过近地点与远地点，在惯性系中的1个轨道周期中，在旋转系中逆行绕月3圈；同理，DRO(4∶1)在惯性系下分别4次经过近地点与远地点。

图21 DRO初始位置对应的轨道周期TFig.21 The period T of the family of DRO as a function of the x0 values

整数比的DRO只是理想情况，它们附近还存在一般意义上的2∶1与3∶1共振轨道，即共振比接近2∶1与3∶1的准共振状态，在地心惯性系下的长期运动轨迹表现为近地点指向的进动，如图25所示。由于篇幅所限，一般意义上的4∶1共振轨道不再列举。

从上述DRO共振特性分析可以看出，较为常规的共振比定义可以得到不同的轨道类型，如DRO与HEO均有2∶1和3∶1共振，但轨道形式具有明显差异。若要能够区分不同类型，需要修改共振比定义。另外，准共振轨道在惯性系中具有近/远地点进动特性，如何描述进动规律仍有待深入分析，若描述进动的参数与共振比值也具有简单整数比现象，那么DRO存在更多、更丰富的共振特性。

图22 整数比DRO(2∶1)共振轨道(左图为地月旋转系，右图为地心惯性系)Fig.22 The integral rate resonant orbit DRO (2∶1) (the left picture plotted in the rotating frame, the right picture plotted in inertial frame)

图23 整数比DRO(3∶1)共振轨道(左图为地月旋转系，右图为地心惯性系)Fig.23 The integral rate resonant orbit DRO (3∶1) (the left picture was plotted in the rotating frame, the right picture was plotted in inertial frame)

图24 整数比DRO(4∶1)共振轨道(左图为地月旋转系，右图为地心惯性系)Fig.24 The integral rate resonant orbit DRO (4∶1) (the left picture was plotted in the rotating frame, the right picture was plotted in inertial frame)

图25 共振比接近但不等于2∶1与3∶1的DRO(左图为2∶1，右图为3∶1)Fig.25 The resonant orbit DRO (the resonant rate nears 2∶1 or 3∶1) (the left picture shows 2∶1 resonant orbit, the right picture shows 3∶1 resonant orbit)

5 圆形限制性三体共振轨道稳定性分析及其潜在应用

在二体模型下，所有的共振轨道都是稳定的，且只与半长轴相关。而在圆形限制性三体模型下，由于月球引力场的引入，极大地复杂了航天器的受力环境，其动力学方程的非线性远远强于二体模型，因此各类共振轨道不都是稳定的，需要用动力系统理论对其的稳定性及其稳定程度做出判断。由动力系统知识可知，周期轨道的稳定性与其Monodromy矩阵密切相关，当M矩阵存在模大于1的特征值时，则该周期轨道不稳定；当M矩阵所有特征值都小于或等于1时，则该周期轨道是稳定的[32]。因此我们可定义L为共振轨道的稳定性指标，L的表达式为式(3)：

L=ln(max(|λi|))

(3)

其中λi是M矩阵的特征值。L的数学含义是对所有特征值的模之最大值取对数，很好地描述了周期轨道的稳定性；若L比0大，那么轨道是不稳定的，比0大得越多，轨道越不稳定；若L在0附近或小于0的话，那么轨道为稳定周期轨道。

5.1 DRO共振轨道

根据轨道周期与稳定性的定义，由地心开普勒1∶1共振轨道延拓所得地月空间DRO的稳定性指标L与相应的轨道周期T如图26所示。

图26 DRO周期轨道族的稳定性及其周期Fig.26 The period T and the stability index L of the family of DRO as a function of the x0 values

图26中横坐标为共振轨道在地月连线上的初始位置x0，纵坐标分别为周期T与稳定参数L，AB两点之间为非开普勒区域，C点(x0=0.73)为稳定区域与不稳定区域分界点。DRO初始位置在地球附近时，它的周期大约为一个月(27天)，与二体下的1∶1共振轨道几乎相同，在理论上不稳定但仍接近稳定状态。当延拓所得DRO接近月球时(x0>0.73)，轨道周期会逐渐变小，形成一个大尺度的稳定逆行绕月轨道。而随着进一步延拓，轨道周期会快速变小从而最终成为主要受月球引力影响的一条近似环月开普勒轨道。

然而，在真实星历下与其它摄动力下，圆形限制性三体模型下的DRO稳定性会发生变化。文献[25]的仿真结果说明：对应部分轨道周期的DRO会产生不稳定的现象(仅考虑圆形限制性三体模型则是稳定的)，其中太阳引力是对稳定性影响最大的摄动力。根据文献[33]的分析，在太阳系各类摄动力下(包括太阳引力、太阳光压与行星引力摄动)，长达500年稳定的DRO(2∶1)的周期区间为T∈[11.4 12.21]∪[12.29 12.78]∪[12.99 13.08](单位：天)，在地月旋转系下如图27所示。文献[34]对DRO的30年稳定性开展了数值仿真研究，用以支持在DRO部署航天器的应用任务。

图27 稳定的DRO(2∶1)准共振周期轨道族示意图Fig.27 The stable DROs (2∶1)

图27中的DRO轨道族在空间任务设计中有其特殊用途。该DRO距离地球较远，部署在DRO的航天器可以避免地球磁场辐射以及空间碎片的影响，并根据任务需求保持与地球的距离。这类性质可用在天体物理中，比如空间光学望远镜。在深空探测任务中，它可以作为从地球到深空的一种中转站，实现不同舱段在此交会对接后进入深空飞往其他行星系[23]。

5.2 HEO(3∶1)共振轨道

同理，3∶1共振轨道中的稳定性指标L与相应的轨道周期如图28所示。已知3∶1共振轨道存在两族轨道，左图显示的是从月球向地球延拓得到的轨道族曲线，右图显示的是从地球向月球延拓得到的轨道族曲线，其中A点(x0=0.4696)是两类轨道族的交集。由左图可知该3∶1共振轨道族初始状态在x0<0.4696时轨道才是稳定的，在x0>0.4696时(包括靠近月球的轨道)都是不稳定的。在月球附近(x0=0.9022)到A点处(x0=0.4696)，共振轨道周期变化并不大，共振比接近3∶1。当从A延拓到地球附近时，轨道周期快速减小，最终趋向于0，因此共振比发生大的变化，成为绕地轨道。右图则表明该轨道族在地球附近与A点之间是不稳定的，其共振比接近3∶1。而当从A点向月球延拓时会形成稳定的周期轨道，周期逐渐增大，最终延拓到x0=0.5398处，周期变为14.3天，共振比接近2∶1。

图28 HEO(3∶1)共振周期轨道族的稳定性及其周期Fig.28 The period T and the stability index L of the family of HEO (3∶1) as a function of the x0 values

当近地点离地球高度只有300 km时(图11～12中的轨道)，HEO(3∶1)不稳定的共振轨道即可接近地球，也可接近月球(离月球低轨道仍有一定距离)，可称之为地月自由往返共振轨道(无法从月球低轨道发射的不是传统意义上的自由往返轨道)。考虑它的不稳定性，在此轨道上的航天器的机动能力强，可以无需消耗工质在地月之间进行转移，通常可作为载人登月的轨道。从地球到月球只需要大约5天，若航天器在向月球的途中发生故障，可直接利用轨道的对称性返回地球。另一个重要的用途在于它是可以实现地球大气再入的轨道，因此出于其它轨道的航天器需要再入大气时可先行转移到该轨道。

若要使初值在月球附近的3∶1共振轨道保持稳定，则需要消耗一定数量的能量。首先我们定义一些函数。在已知延拓出的3∶1平面共振轨道的初值下定义V0=P1(x0)，即初始位置对应的初始速度。之后，将这个初始状态数值积分近3个轨道周期，即大约一个季度的时间，当它第三次经过靠近月球的地月连线时，记录此时航天器的位置xt与速度Vt，定义Vt=P2(xt)与映射xt=Σ(x0)，如图29所示。

图29 HEO(3∶1)共振轨道在地月旋转系下函数与映射示意图Fig.29 The resonant orbit HEO (3∶1) in the rotating frame and its mappings

由函数的定义可知，当航天器在初始位置x0经过运动映射到初始位置x时，需要施加速度脉冲dv(x)=|P2(x)-P1(x)|即可进入初始位置为x的3∶1共振轨道。而Σ(x)通过数值计算可得，因此具体的轨道保持过程可由图30所示。

图30 HEO(3∶1)共振轨道由映射所表示的轨道保持示意图Fig.30 The orbital maintenance of the resonant orbit HEO (3∶1) from the mappings

图30中的直线xt=x是一条斜率为45°的直线。根据映射Σ(x)可知初始位置在A1的航天器将要运动到A2处，施加速度脉冲大小为dv2后将运动到A3处，依次类推，它可以逐渐过渡到初始位置逐渐远离月球的3∶1共振轨道上。图30中总共施加速度脉冲16次，轨道维持大约4年，总消耗不超过130 m/s。在此期间航天器近月点移动不超过6 km。

5.3 HEO(2∶1)共振轨道

同理，2∶1共振轨道中的稳定参数L与相应的周期如图31所示。两类2∶1共振轨道族的初始位置分别存在于区间I(x0∈[0.005304 0.5399])与区间II(x0∈[0.8645 0.9724])。其它范围的共振轨道都无法延拓得出，因此两类轨道族没有关联。初始位置处于区间I中的轨道都是稳定的(L的值几乎为0)；初始位置处于区间II的轨道是不稳定的(L的值均大于4)，且轨道周期要大于区间I中的轨道周期。

图31 HEO(2∶1)共振周期轨道族的稳定性及其周期Fig.31 The period T and the stability index L of the family of HEO (2∶1) as a function of the x0 values

该轨道处于区间II，是不稳定的周期轨道，远地点为34×104km，近地点为13×104km。特殊之处在于它的轨道周期为29.25天，恰好比月球轨道周期(27天)多出1/12。每一个月球周期远地点会逆时针进动30°，即一年时间内远地点方向绕地球一周，可称之为拱线太阳同步共振轨道。如图32所示。拱线进动太阳同步共振轨道在科学研究中具有潜在应用价值，比如观测太阳与地磁场，研究太阳风对地球磁场的影响[35]。由于该轨道是不稳定的，需要进行轨道维持，维持方法与3∶1共振轨道一致。

图32 线拱线进动太阳同步共振轨道(左图为地月旋转系，右图为地心惯性系)Fig.32 The periapsis Sun-synchronous resonant orbit (the left picture was plotted in the rotating frame, the right picture was plotted in inertial frame)

6 结论

本文分析了在圆形限制性三体模型下DRO与HEO(2∶1/3∶1)共振轨道的特性(包括稳定特性与共振比变化)。通过对二体模型下开普勒共振轨道初始状态延拓求解得到DRO及HEO。利用动力系统理论稳定性分析方法，给定了DRO及HEO(2∶1/3∶1)的稳定范围。根据相对地球与月球的能量E的变化确定DRO非开普勒区域，发现非开普勒区域中的DRO周期发生大的变化(其中存在2∶1、3∶1与4∶1的共振轨道)。HEO(3∶1)呈现出近地轨道与月球的往返方案，选择合适的轨道能实现地月之间的货运或载人往返，初步估计了地月往返轨道[HEO(3∶1)]维持所需的能量消耗(4年不超过130 m/s速度脉冲)。HEO(2∶1)根据其两类延拓结果可分为稳定轨道与不稳定轨道两个区间，其中不稳定轨道中存在拱线太阳同步共振轨道，能用来探测太阳磁场在地月空间中的分布；根据本文的分析，DRO与HEO(2∶1/3∶1)在空间探测中有着潜在应用价值，有待进一步研究探讨。