基于能量范数的EFG方法权函数影响半径的研究

贾亚茹,付 伟,曹 健

(太原科技大学应用科学学院,山西 太原 030024)

无网格方法是近年来兴起的一种数值计算方法。1994年,Belyschko等人[1]通过采用MLS法计算形函数,并利用Lagrange乘子法引入本质边界条件,提出了无单元伽辽金法(EFG),改进了之前Nayroles等[2]提出的弥散单元法(DEM),提高了算法质量,为无网格方法的发展迈出了关键一步,掀起了无网格方法研究的热潮。使用MLS方法构造形函数时,所得到的最后的代数方程组有可能是病态的,导致得不到理想的数值解。2013年,顾天奇、张雷等人[3]提出了改进的MLS方法,解决了这一问题。2013年,张赞等人[4]提出了关于三维瞬态热传导问题的改进无网格伽辽金法。2014年,王聚丰、程玉民等人[5]对插值型移动最小二乘法进行了误差估计,得出结论,如果多项式基函数的阶足够大且原始函数足够光滑,则逼近函数及其偏导数在影响域的最大半径上收敛到精确值。2015年,孙凤欣等人[6]在n维空间内对插值型最小二乘法进行了误差估计,在王聚丰、程玉民等人的基础上提出了基于IMLS方法的插值无单元Galerkin(IEFG)方法。2018年,蔡小杰等人[7]建立了弹塑性大变形问题的改进的无单元Galerkin方法,此方法是基于改进的移动最小二乘法建立形函数,根据弹塑性大变形问题的Galerkin弱形式建立离散方程,利用罚函数法施加位移边界条件,推导了弹塑性大变形问题的改进的无单元Galerkin方法的公式,采用Newton-Raphson迭代法进行求解。

无网格法发展短短数年,虽为工程计算问题带来一些新方法所具有的变革,但事实上是远远不够的,其中还有一些不足和有待研究者来解决的问题。

本文介绍了无单元伽辽金方法中构造形函数的方法——移动最小二乘法,重点探究了权函数的影响半径对无网格方法精度的影响。结合权函数的性质和形式,分析了权函数的影响半径对于数值结果的影响,给出了结合参数构造的新的权函数的影响半径的确定方法和基于能量范数的误差模型。通过对比不同参数值下的误差的能量范数,得出最优的参数值,从而确定权函数的影响半径的取值,并对实际的数值算例进行了研究,通过设定不同积分网格分布下的Laplace方程和Poisson方程对数值结果进行分析,结合数值算例证明了给出的新的权函数的影响半径的确定方法的有效性。

1 移动最小二乘法(MLS)

无单元伽辽金方法中运用移动最小二乘法确定形函数。移动最小二乘法的优势在于可以通过不同阶数的基函数和不同的权函数提高移动最小二乘近似的计算精度[8]。

在移动最小二乘法(MLS)中,函数u(X)近似为:

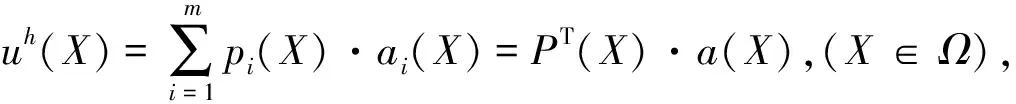
(1)

这里m是基函数的个数,PT(X)是基函数,a(X)是相应的系数。

基函数在二维空间的形式为:

线性基:

PT(X)=[1,x,y]

(2)

二次基:

PT(X)=[1,x,y,x2,xy,y2]

(3)

定义如下函数:

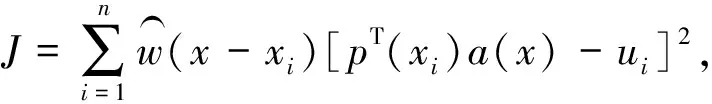
(4)

对加权残量泛函J关于a(x)求偏导,

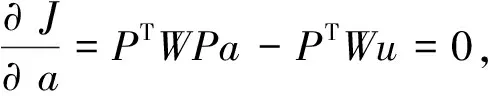
(5)

令式(5)中,

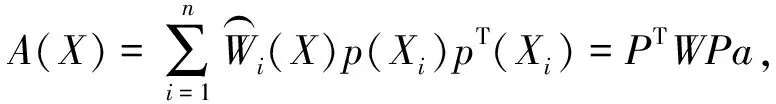
(6)

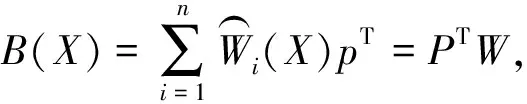
(7)

从而有

A(X)a(X)=B(X)Us,

(8)

其中,Us={u1,u2,…,un}T为积分域中所有节点形成的节点参数向量。

针对一个二维问题,选取线性基作为基函数,

(9)

(10)

根据移动最小二乘法(MLS)可得到逼近函数uh(X)的表达式为:

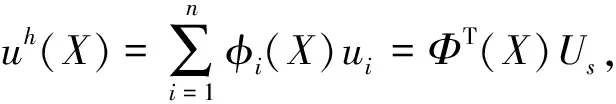
(11)

其中，ΦT(X)定义为点x所在的积分单元内所有节点的MLS形函数,具体表示为:

(12)

在移动最小二乘法中,求解的关键之一在于需要通过合理控制支持域中节点的数量来保证A的可逆性,从而获得MLS法的稳定性。另外,待定系数a(X)是一个关于X的函数,这就使得整个未知函数的拟合近似成为一个动态过程,同时在定义域内也具有了连续性。以上结论都是建立在选取了合适的权函数,由此说明,在MLS方法中权函数对于数值结果的质量有着极为重要的影响。

1.1 权函数的性质

权函数的选取应根据以下几方面的性质来提升整个算法的动态性,支持MLS法的相容性[9]。

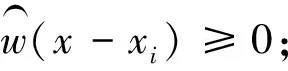
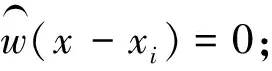
在这几个性质中,紧支性是最重要的,它对于局部区域数值的控制使得近似成为可能。

1.2 权函数的形式

权函数的形式多种多样,目前常用的权函数有指数型、Gauss型、样条函数等。在解决实际问题时应注重权函数的改变为算法带来的精度影响。

1)指数函数

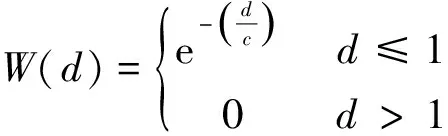
(13)

2)Gauss函数

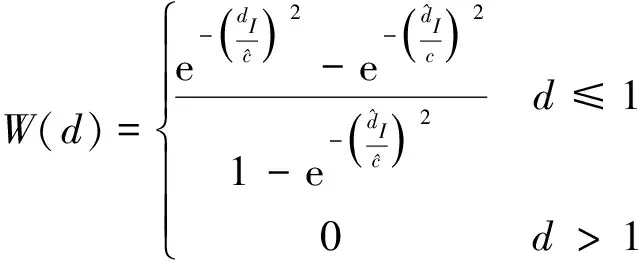
(14)

3)三次样条函数

(15)

4)四次样条函数

(16)

MLS近似法可以非常接近于内插方法(局部近似)或类似于传统最小二乘法近似(全局近似),这都要取决于所采用的权函数的影响半径。要使得MLS近似更加精确,对每个权函数影响范围的重叠区域要有足够的要求,同时要保证影响域内有足够的节点数量。权函数的影响半径选取要使得影响域内节点数量不能出现太多或太少的情况,一方面要求影响域内的节点数量应足够多,这是为了保证矩阵A(x)的可逆性,另一方面保证影响半径足够小,MLS方法是一种注重局部特性的研究方法,过大的影响域会使得拟合效果失真,计算效率降低,为此保证影响半径足够小也是提高拟合效果的重要方法。

2 误差估计

本文使用相同的权函数,在不同的影响半径下使用无网格伽辽金法来计算得到的不同的近似结果。

定义是三个影响半径rinf-min,rinf,rinf-max:

1)rinf:rinf=α×dI,其中dI为距离节点I第n个最近节点的距离,α为正实数。

2)rinf-min:rinf-min=prod×dI,其中prod∈∪(1.5,δ)。

3)rinf-max:rinf-max=β×rinf-min,其中β∈∪(2,δ)。

2.1 误差公式的定义

误差,定义为近似解与精确解之间的差异。无网格伽辽金法大多被应用于解决工程力学方面的实际问题,其中会产生位移和应变两个值,而应变的误差研究比位移更重要,因为通过大量的数值计算发现位移所表现的误差没有应变反应的误差更灵敏,所以这里采用能量范数误差对每个积分单元进行误差估计。

本文的重点在于,通过误差的变化来确定参数prod、β的取值,从而获得最优误差下的影响半径。

2.2 误差范数

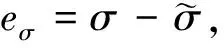
(17)

误差的能量范数为:

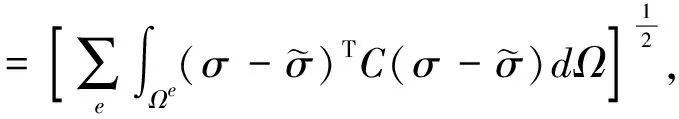
(18)

对于每个单元,有

(19)

结构的总体能量范数

(20)

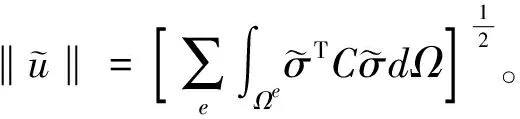
2.3 误差指标

总体误差指标以η表示,则

(21)

对于每个单元,误差指标

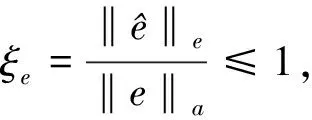
(22)

其中,‖e‖a是单元应力误差能量范数‖e‖e的允许值。

3 数值算例

3.1 数值算例1——矩形域上的Laplace方程

选取Laplace方程作为算例,通过判断误差的大小对新的影响办法选取方法进行可行性检验。

方程为:

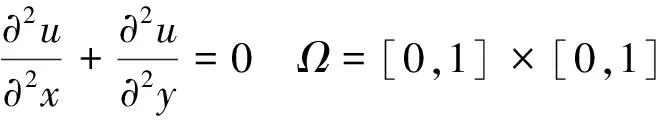
(23)

边界条件:

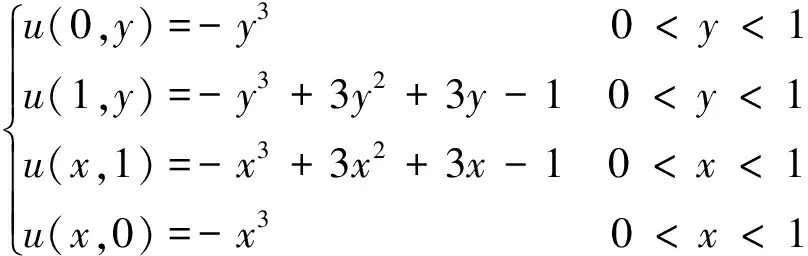
(24)

解析解:

u(x,y)=-x3-y3+3x2y+3xy2

(25)

在本算例中,选取四次样条权函数,惩罚因子为1015,矩形域[0,1]×[0,1]内分别均匀分布了三种节点:15×15,25×25,35×35,采用的背景网格与节点分布相同。在影响半径rinf-min=prod×dI中,令dI=1。

为了确定prod和β对于误差的影响,本文分别对这两个参数进行了研究:

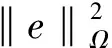
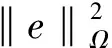
3.1.1参数prod的确定

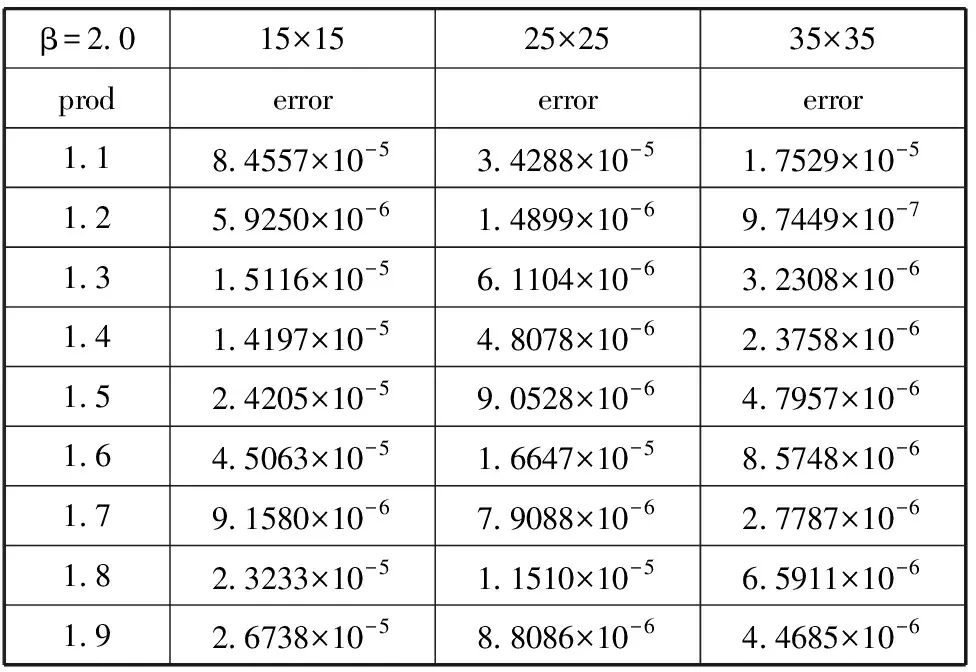
表1 prod取不同值,β=2.0时的能量范数误差

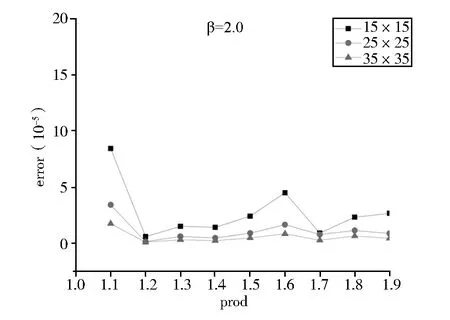
图1 prod取不同值,β=2.0时,不同节点下的能量范数误差

由图1可以看出,在三种不同的网格划分下,参数prod在1.2处都处于曲线的最低点,能量范数误差在prod=1.2时取得最优值。同时,也可以看出网格划分越多,节点密度越大,能量范数误差越小,数值的近似结果越精准。

3.1.2参数β的确定

表2 β取不同值,prod=1.2时的能量范数误差

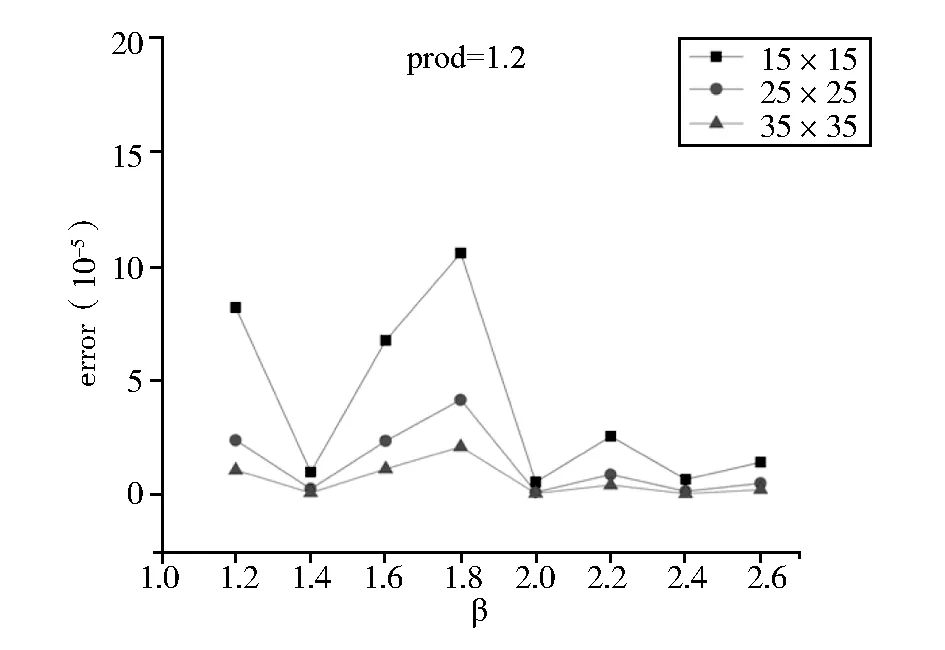
图2 β取不同值,prod=1.2时,不同节点下的能量范数误差

由图2可以看出,能量范数误差在β=2.0时达到最优,同时网格划分密度越大,能量范数误差越小,数值近似结果越精确。

3.2 数值算例2——矩形域上的Poisson方程

方程为:

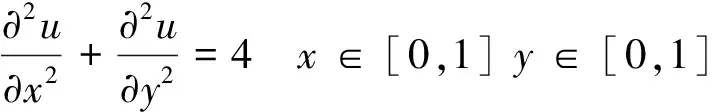
(26)

边界条件为:

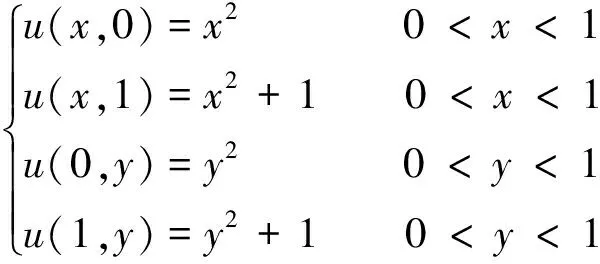
(27)

解析解为:

u(x,y)=x2+y2

(28)

在本算例中,选取四次样条权函数,惩罚因子为1015,矩形域[0,1]×[0,1]内分别均匀分布了三种节点:15×15,25×25,35×35,采用的背景网格与节点分布相同。在影响半径rinf-min=prod×dI中,令dI=1。

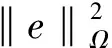
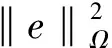
3.2.1参数prod的确定

表3 prod取不同值,β=2.2时的能量范数误差

图3 prod取不同值,β=2.2时,不同节点下的能量范数误差

由图3可以看出,在三种不同的网格划分下,参数prod在1.4处都处于曲线的最低点,能量范数误差在prod=1.4时取得最优值。同时,也可以看出网格划分越多,节点密度越大,能量范数误差越小,数值的近似结果越精准。

3.2.2参数β的确定

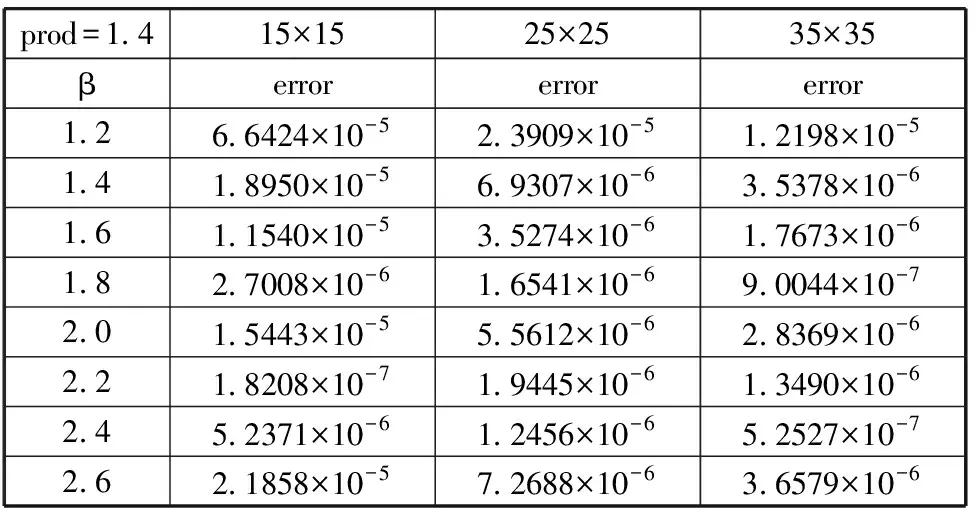
表4 β取不同值,prod=1.4时的能量范数误差

图4 β取不同值,prod=1.4时,不同节点下的能量范数误差

由图4可以看出,在三种不同的网格划分下,参数β在2.2处都处于曲线的最低点,能量范数误差在β=2.2时取得最优值。同时,也可以看出网格划分越多,节点密度越大,能量范数误差越小,数值的近似结果越精准。

4 结论

此误差估计方法是以每个积分单元为单位进行的,可以提高准确性和有效性。

通过以上两个数值算例的结果所示,当β的取值在[2.0,2.2]之间,prod的取值在[1.2,1.4]之间时,数值算例中在不同节点划分下的能量范数误差达到最小值。同时,通过数值算例的分析研究可以看出,合理调整节点和几分单元的划分可以增强数值结果的精度。总的来说,适当增加节点的密度划分获得的误差结果越小,近似结果的准确度越高。

选取合适的权函数的影响半径对EFG方法的精度有重要影响,同时对误差的估计有助于调整节点和积分单元的划分,从而增强结果的准确性。本文提出的确定权函数影响半径的方法,通过了实际的数值算例验证了此方法的合理性,证明了使用此方法可以在问题域中得到较为理想的结果。