基于替代模型的地表水地下水耦合模型不确定性分析

韩 玉，卢文喜，张将伟，安永凯

(1.吉林大学 地下水与资源环境教育部重点实验室,吉林 长春 130012；2.吉林大学 环境与资源学院,吉林 长春 130012)

0 引 言

地表水和地下水是水资源的重要组成部分，两者之间相互作用，具有密切的水力联系。在对区域水资源的评价管理过程中，两者之间的联系常常被简化，为解决这一问题，本文建立了地表水地下水耦合模拟模型对地表水和地下水的水流运动及两者之间的水力联系进行描述。与此同时，在对源汇项的概化过程中，由于主观与客观因素的影响，使得人工开采的不确定性较大，对研究区地表水地下水的耦合模型输出结果会产生一定的影响。为评估模拟模型的输出结果的可靠性，考虑地下水开采量的不确定性及可能造成的风险对于区域水资源的开发利用具有重要的意义。

近年来，模型的不确定性分析已经得到了人们的广泛关注。1968年，Yen等人对水文模型的不确定性进行分类[1]，为不确定性的研究提供理论依据；Lopes等人将降雨的空间差异性与流域径流量的变化情况进行结合，研究降雨空间分布的不确定性[2]，具有实际意义；2012年，Harp和Vesselinov采用水文地质接受概率的方法对水文地质统计模型的不确定性进行综合分析，为不确定性分析提供一个新的方向[3]；苗添升在2016年结合实际例子对研究区地下水水流模拟模型的不确定性进行分析[4]。但不确定性分析大多应用于地下水水流的数值模拟中[5]，对于地表水地下水的耦合模拟方面的应用较少。在耦合模拟模型的不确定分析过程中，模拟模型的调动次数过多，计算时间较长。为解决这一问题，应用Kriging模型建立地表水地下水耦合模拟模型的替代模型，解决了不确定分析过程中计算负荷较大的问题。

在建立地表水地下水耦合模拟数学模型的基础上，对地下水开采量进行不确定性分析。采用拉丁超立方抽样抽取均匀分布的地下水抽水量数据集，将其带入已建立的地下水地表水耦合模拟模型中，运行HydroGeoSphere软件得到相应的地表水径流量和地下水水位，通过输入输出数据集对Kriging模型进行学习训练，从而得到地表水地下水耦合模拟模型的替代模型。按照相同的方式抽取样本容量足够大的地下水井开采量数据，借助替代模型得到相应的地表径流量和地下水水位输出数据，借助切比雪夫不等式，计算不同置信度下地表径流量与地下水水位的置信区间。最后通过绘制累积概率分布图，结合地下水生态水位阈值对研究区的地下水水位进行风险评估。

1 研究方法

1.1 模型建立

建立一个三维的非稳定潜水含水层的假想研究区，研究区两侧高，中间低，河流自南侧流入，北侧流出。

1.1.1 概念模型

(1)边界概化。含水层均质各向同性，北侧Γ1与下游湖泊相连接，水位稳定为28 m，南侧Γ3与上游河流连同，地下水水位保持在68 m左右，东侧Γ4和西侧Γ2为隔水边界；对于地表水水流，上游河口S1为定流量边界，下游河口S2为临界水深边界条件。

图1 研究区边界示意图Fig.1 The schematic diagram of study area boundary

(2)参数分区及赋值。对研究区的地表水水流和地下水水流进行参数分区，分区情况如图2所示，具体赋值情况见表1。

表1 研究区地下水水文地质参数值Tab.1 Groundwater Hydrogeology parameter initial values of study area

(3)源汇项。研究区接受大气降水补给，研究区的主要排泄方式为蒸发排泄和人工开采。现在研究区内设置3口抽水井，2个地表水地表水观测点和21口地下水观测井，对地表径流量与地下水水位进行数据的采集，各井的分布情况如图1所示。模拟时长为3个月，为降水较为充沛的5，6，7月，本次研究对模型运行3个月后的结果进行分析计算。

表2 研究区地表水力参数值Tab.2 Initial values of surface hydraulic parameter

1.1.2 数学模型

采用三维Richard方程和扩散波近似的二维平均深度圣维南(Saint Venant)方程描述地下水水流和地表水水流运动，采用双重节点法对地表水与地下水模型进行耦合，通过达西流关系描述地表水系统与地下水系统的交换量，得到如下微分方程，定解条件和耦合方程：

图2 地表水与地下水的参数分区图Fig.2 Distribution map of hydrogeology parameter of groundwater and surface water

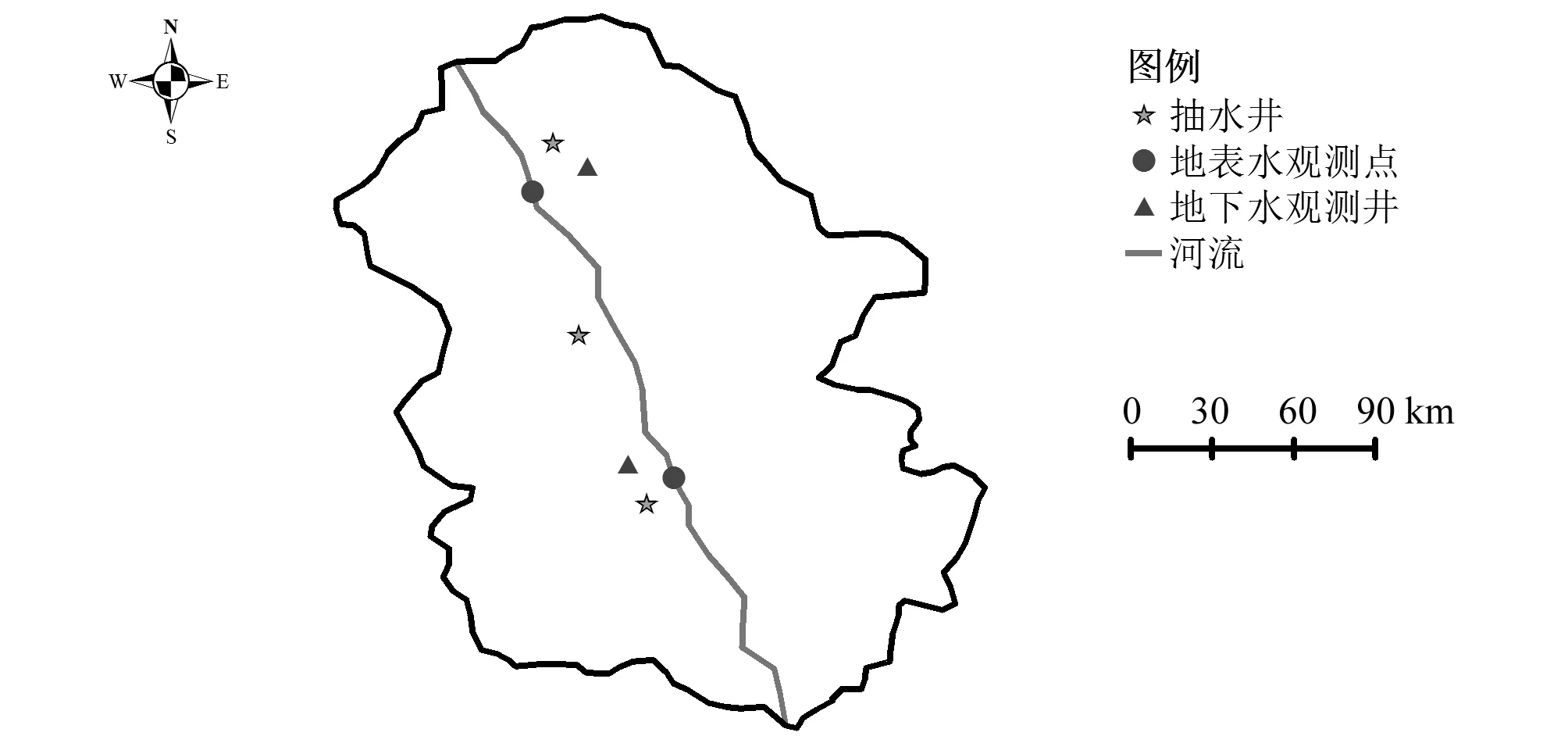
图3 研究区抽水井与观测井分布图Fig.3 Distribution of pumping and observation wells in the study area

(1)

式中：K为渗透系数，[LT-1]；kr为相对渗透率，用以表征包气带对地表水地下水交换的影响；H为地下水的水头，[L]；h1为已知地下水水位，[L]；h为地表水水头，[L]；qgs为地表水与地下水的交换量，[T-1]；QG为地下水的源汇项，[L3L-3T-1]；Sw为饱和度；SS为储水系数，[L-1]；θs为孔隙度；Kox,Koy为x,y方向上的地表传导系数，[LT-1]；ho为地表水面高程，[L]；Q为地表水的源汇项，[LT-1]；φ为地表水等效孔隙度；Kn为边界法方向的地表传导系数，[LT-1]；qo1为第二类边界条件，[LT-1]；qo2为临界深度边界条件，[LT-1]；h为边界水头，[L]；S1,S2为地表水边界；Γ1,Γ2,Γ3,Γ4为地下水边界；lexch为地表水地下水耦合长度，[L]。

1.2 Kriging方法

替代模型也称为“元模型”，能够以简单的程序算法替代复杂繁琐的系统运行过程，从而大幅度的减少实际系统的运算负荷。Kriging方法是一种通过已知点的相关信息来预测未知点的插值方法[6]，能够较好的反映模拟模型的输入输出关系。Kriging方法的输入为抽水井的开采量，输出则为地表观测点的径流量与地下观测井的水位。

Kriging模型的数学表达式是：

y(x)=βfT(xi)+ε(xi)

(2)

式中：f(xi)=[f1(x),…,fk(x)]T为已知的回归函数的基函数，β=(β1,…,βk)T为相应的未知参数，ε(xi)为高斯随机过程，其均值为0，方差为σ2，协方差为：

Cov[ε(xi),ε(xj)]=σ2R(xi,xj)

(3)

式中：R(xi,xj)为空间采样点xi,xj的相关函数，可以采用以下函数形式进行表示：

(4)

由已知n个样本点[X]=({X1}T,…, {Xn}T)T的响应[y]=(y1,…,yn)T来预测任一点{x*}的响应：

(5)

式中：rT(x)=[R(x*,x1),…,R(x*,xn)]，[R]为矩阵元素为R(xi,xj)的(n×n)矩阵。

1.3 Monte Carlo模拟

Monte Carlo方法又称为统计模拟方法，是一种常用的数值模拟的不确定性分析方法，在解决非线性的随机问题的过程中具有一定的优势[7]。

(1)采用拉丁超立方抽样方法对地下水开采量进行随机抽样，将样本数据作为输入数据集；

(2)在地表水地下水耦合模拟模型的基础上，通过HydroGeoSphere软件进行并行同步求解，得到输出量(如地表水径流量和地下水水位)的数据集；

(3)对输出结果进行统计分析，得到方差，均值，极大值，极小值等估计量，并用统计结果绘制图表，根据概率分布情况进行不确定性分析。

2 结果与讨论

2.1 Kriging替代模型

采用拉丁超立方抽样方法得到50组均匀分布的开采量样本数据，将其作为输入值，运行HydroGeoSphere软件，得到相对应的地表水径流量和地下水位降深作为输出值，选取前40组输入-输出样本作为训练样本，得到耦合模拟的替代模型；将后10组的输入-输出样本对替代模型进行检验，结果见图4。

图4 替代模型检验样本误差Fig.4 The relative error of the test sample for the surrogate model

从图4可以看出，1号地表水观测点和1号地下水观测井的相对误差波动幅度较小，2号地下水观测井的相对误差波动幅度较大，认为在河流入口处地下水开采对于地表径流的影响较小，出口处的地下水降深受地下开采的影响较为明显。但总体变化较小，一般小于0.1%。说明替代模型的结果能够很好地逼近地表水地下水耦合模拟模型的运行结果，且精度较高。

2.2 不确定性分析

2.2.1 统计分析

使用SPSS软件的K-S检验对各地表水观测点和地下水观测井的数据进行统计分析，得到地表径流量与地下水位的频率分布直方图，结果显示，2号地表水观测点的径流量的分布较集中，服从均值为0.243，标准差为0.026的正态分布，径流量波动范围是0.235～0.246，地下水观测井的水位分布不服从正态分布，认为地下水水位的分布未知。

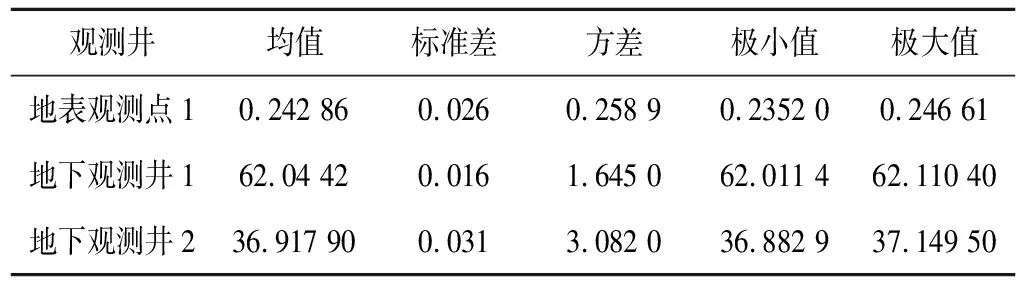
表3 不同观测井的统计结果Tab.3 Statistics of different observation wells

图5 地表水观测点径流量的频率分布直方图Fig.5 Frequency distribution histogram of the runoff at the observation point

图6 地下水观测井水位降深的频率分布直方图Fig.6 Frequency distribution histogram of water level deepens in groundwater observation wells

由表3可以看出，地表观测点径流量的均值偏向极大值，地表水水位降深的均值偏向于极小值，说明在相同的水利条件下，地表径流量的变化情况比地下水位降深的变化情况更为明显；结合图5和图6可以看出，地下水的方差较大，数据离散化较明显，故地下水的不确定性较大。

2.2.2 区间估计

置信区间或称置信间距，是指在某一置信度时，总体参数所在的区域距离或区域长度[8]。置信度又称显著性水平，是指估计总体参数落在某一区间时，可能发生错误的概率。由于地表水径流的分布已知，可以采用概率密度函数对其进行进一步的分析计算，而地下水的分布情况未知，故采用切比雪夫不等式对其分布情况进行确认和计算。

切比雪夫不等式是概率不等式的一种，利用随机变量的数学期待和方差计算不同置信度下的区间范围，适用于概率分布未知但方差已知的随机变量的区间估计。

表4 不同置信水平下地表径流量和地下水位的区间估计Tab.4 Interval estimation of surface runoff and groundwater depth at different confidence levels

在估计总体参数时，一般都会给出一个较高的置信度。本文通过替代模型获得样本容量为1 000的地表水径流量和地下水水位数据，通过表4可以看出置信度越高，置信区间就越大，即估计的参数的相对精度就会越低。反之，置信度越低，则精度相对就会越高，并且区间集中于均值附近。

2.2.3 风险评估

对地下水的水位进行统计分析，并据此绘制累积概率分布图如图7所示。

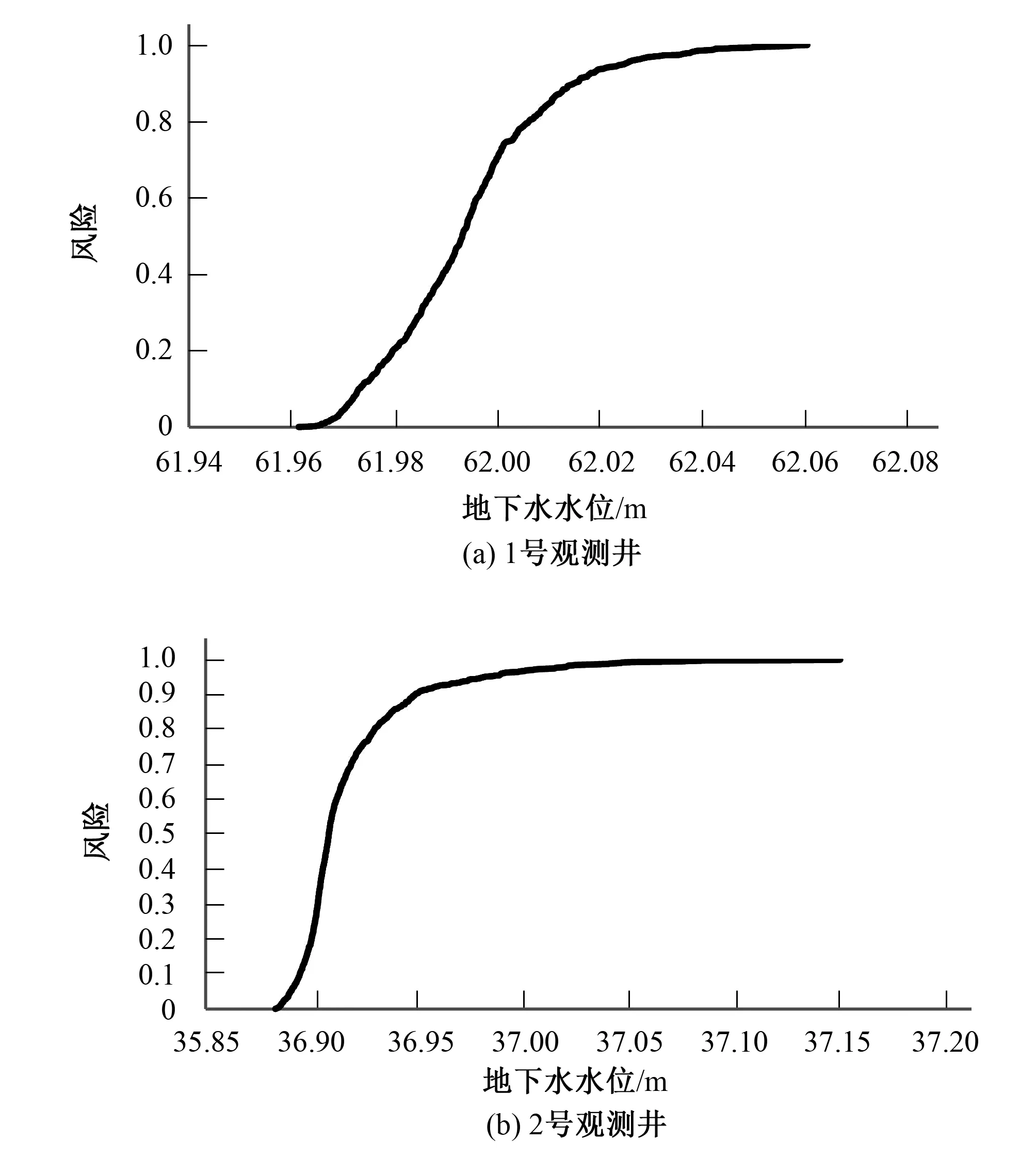
图7 各地下水观测井水位累积概率分布图Fig.7 Probability distribution of water level in groundwater observation wells

地下水观测井沿着河流两侧自上而下分布，当1号和2号地下水观测井同时满足地下水水位分别低于62 m和37 m的条件时，该研究区的浅层地下水处于疏干状态，继续抽水会造成研究区水生态的恶化。

根据各地下水观测井水位的累积概率分布图可以看出，1号地下水观测井水位低于62 m的风险是0.6，2号地下水观测井水位低于37 m的风险为0.2，沿河分布的两口观测井的风险值明显下降，地下水受到地表水的补给，水位上升，地表水于地下水之间存在水力联系。综合考虑研究区的用水需求，认为地下水开采造成研究区水环境失衡的风险为0.2。

2.3 运算负荷分析

研究区地表水地下水联合模拟模型在CPU为Intel Core i5-4430，内存为4GB，操作系统为Windows 10 的计算机上，运行一次需要的时间大约为12 600 s(约3.5 h)。假设后续对地表水地下水耦合模拟模型进行不确定性分析时，需要反复调用该模型1 000次，则运行消耗的总时长约146 d。如果通过所建立的替代模型来进行计算，仅需要在前期调用50次耦合模拟模型来建立模拟模型的替代模型，耗时约7天，然后利用替代模型来进行不确定分析，耗时为5 s，总耗时为11 d。结果表明，替代模型能够大幅度减小计算负荷和计算时间。

3 结 论

(1)采用Kriging方法建立模拟模型的替代模型，运行结果能够充分逼近模拟模型的输入输出关系，能够大幅度的减少不确定分析过程中的计算负荷。

(2)结合累积概率密度曲线对较高置信度下地下水位区间进行风险评估，发现随着地表径流和降水入渗的补给，河口地表水水位抬升，对地下水进行补给，地表水与地下水之间存在水力联系和相互转换作用。

(3)在模拟模型替代模型的基础上，对地表水地下水耦合模拟模型的源汇项进行不确定性分析，可以定性地对模型输出结果的可靠性进行分析，为决策者提供参考，对于区域水资源开发利用提供科学依据。