外方内双螺旋箍筋约束混凝土柱轴压承载力计算方法
黄永安
(中铁第一勘察设计院集团有限公司,西安 710043)
1 概述
地铁车辆基地上盖物业综合体在我国发展较快,引起政府部门及设计界同行的广泛关注。在国际城市规划中,地铁上盖物业已成为发展潜力最大、使用程度最高、抗风险能力最强的城市高效物业形式。随着建筑结构形式的快速发展,地铁车辆基地上盖商业城市综合体底层框架结构需要承受巨大的轴向压力。若采用传统钢筋混凝土结构,势必会增大框架柱截面尺寸,对车辆基地底层工艺设备布置以及空间利用均将产生显著影响。更为重要的是增大截面尺寸会显著降低混凝土构件的延性,增加了脆性破坏的可能性[1-5],较难满足建筑物对抗震设防的设计需求。针对这一工程现状,提出了外方内双螺旋箍筋约束混凝土柱,它是一种在普通矩形箍筋混凝土柱基础上,内部增加两层螺旋箍筋形成的新型结构形式。
国内外学者对约束混凝土开展了大量研究并取得了丰硕成果[6-11],但绝大多数是针对单层箍筋约束或者钢管混凝土,对多重箍筋约束形式下的混凝土受力性能研究相对较少。相比单层箍筋约束混凝土和钢管混凝土,多层箍筋约束混凝土柱具有强度高、延性好、造价低廉等优点,在提供高承载力的同时可以显著减小混凝土柱截面尺寸。鉴于多重约束混凝土柱受力性能的复杂性,不能完全按照传统约束混凝土柱计算方法计算,使得其应用受到了一定的限制。因此,基于已有约束混凝土基本理论,建立外方内双螺旋箍筋约束混凝土柱的约束模型并给出了基本假定,采用叠加原理和统一强度理论,分析各部件的受力状态,理论推导出该新型约束结构柱的轴压承载力计算公式,并通过有限元分析加以验证,以期为实际工程应用需要提供理论参考。
2 约束模型
外方内双螺旋箍筋约束混凝土柱的截面形式如图1所示。图1中外层为普通矩形箍筋,内层分别布置了两层不同直径的螺旋箍筋,并将纵筋依次布置在螺旋箍筋构成的圆周边上,由此将整个截面分成了3块约束程度不同的区域,从而形成具有多重箍筋约束的钢筋混凝土柱。

图1 外方内双螺旋箍筋约束混凝土柱截面配筋
基于有效核芯混凝土约束模型,提出“外矩形内双螺旋箍筋约束混凝土柱”轴压约束模型,如图2所示。
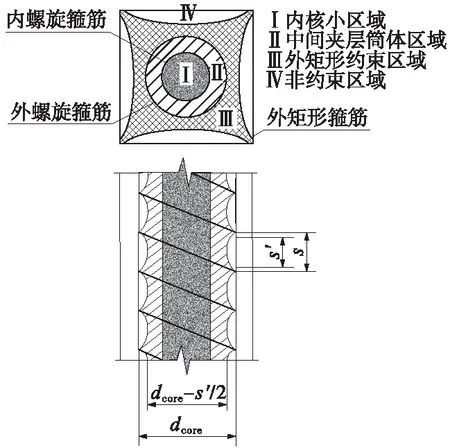
图2 约束模型
3 极限轴压承载力分析
3.1 基本假设
(1)简化分析时不考虑各元件之间的相互作用。
(2)外螺旋以外部分,认为此部分强度足够,破坏极限为各元件同时达到破坏强度,且螺旋箍筋都已屈服。
(3)螺旋箍筋对混凝土有稳定的围压力,不考虑螺旋箍筋与混凝土之间滑移影响。
(4)由约束模型可将构件截面划分为4部分,分别为内核芯区域、中间夹层筒体区域、外矩形箍筋有效约束区域和外矩形箍筋非有效约束区域。该类新型构件的极限轴压承载力由各部分元件以及纵筋的承载力叠加而得到。
3.2 中间夹层筒体区域II的强度计算
混凝土筒体截面受力如图3所示,其内外围压力分别假定为Pi和Po。筒体外部受到外螺旋约束,由静力平衡方程[12]可得混凝土筒体外围约束力为(假定箍筋发生屈服)
(1)
考虑到筒体外围还有部分混凝土的约束作用,且较难直接计算此部分提供的围压力,故取一围压增大系数ψ,弥补这一影响。ψ取1.2,则筒体实际外围压大小为
Po=ψflo=1.2flo
(2)

图3 筒体截面受力示意
由于筒体混凝土区域处于三轴受压状态,故筒体混凝土抗压强度fcc外可采用Mander[9]提出的强度公式进行计算
(3)
式中,fcc外为约束混凝土的抗压强度;fco为无约束混凝土的抗压强度;fle为作用于核芯混凝土的有效侧向约束应力,按下式计算
fle=kefl
(4)
其中,ke为约束效用系数;fl为横向箍筋施加在核心混凝土上的侧向约束力
fl=Po=1.2flo
(5)
根据有效约束混凝土理论,对于螺旋箍筋ke定义为
(6)
式中,Ae为有效核心混凝土面积;Acc为外围螺旋箍筋包围的不包括纵向钢筋的核心混凝土面积;ρcc为纵向钢筋截面与去掉纵筋的核芯混凝土面积之比。公式中相关参量定义如图4所示。
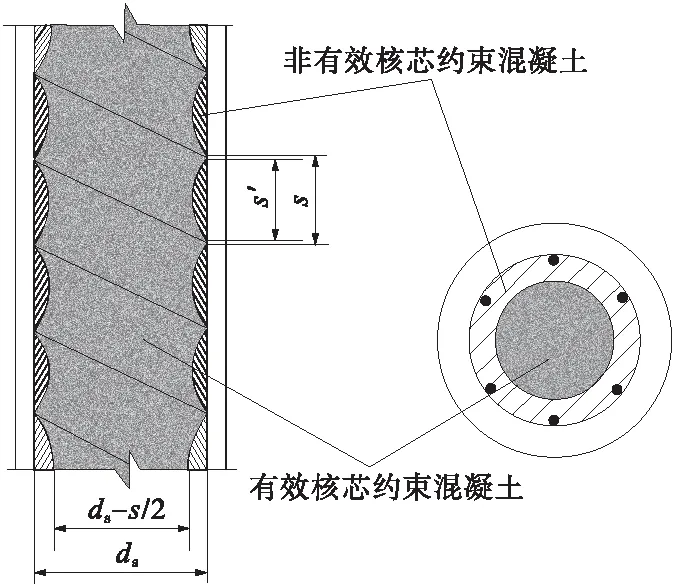
图4 筒体截面受力示意
3.3 内核芯区域I强度计算
由于内核芯混凝土处于环向均匀的三轴受压约束状态,其极限强度可根据Richart强度模型[13]计算
fcc=fc+kfl
(7)
式中,fc为无围压时混凝土轴心抗压强度;fl为环向约束力;k为约束应力系数。
对于内核芯环向约束力fl的求解,根据配筋构造和约束模型,可认为其由两部分组成:①螺旋箍筋提供的约束力fl1;②混凝土筒体提供的均匀围压fl2。
对于螺旋箍筋提供的约束力fl1,由静力平衡法[12]可得
(8)
式中,fy为箍筋屈服强度;Asp为单根箍筋的横截面积;s为螺旋间距;dcor为核芯直径,以箍筋内表面确定。
对于混凝土筒体提供的均匀围压fl2,根据相互作用力,其等于混凝土筒体内部受到的挤压Pi,即
fl2=Pi
(9)
对于内外受均匀围压的筒体结构,采用拉梅理论,进行其内部应力的求解。混凝土筒体的受力简图以及微元体受力见图5,其径向应力与环向应力的数学表达式分别为

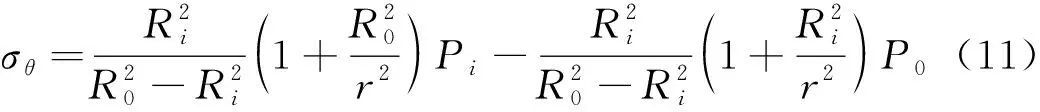
式中,Ri、R0分别为筒体内、外半径;r为圆筒内任意一点距圆心的距离。

图5 混凝土筒体及其微元受力简图
对于此混凝土筒体,破坏时认为首先是在圆筒内壁屈服,取筒体内壁应力块,由于小微元,取r=Ri。则由公式(10)和公式(11),可得内壁应力块应力为
(12)
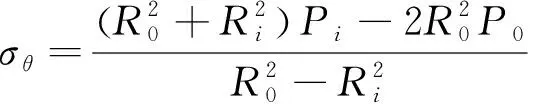
(13)
此外,圆筒在轴压力作用下还将产生压应力σz,应用考虑中间主应力和材料拉压比影响的统一强度理论[14],其表达式如下

(14)

(15)
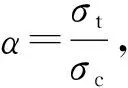
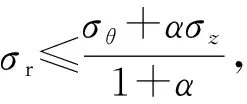
(16)
将式(12)、式(13)代入式(16),得

(17)
化简后可得
(18)

则有
(19)
故由式(8)、式(9)、式(19)可得内核心混凝土的全围压力为
fl=fl1+fl2
(20)
根据式(7)得核芯混凝土轴心抗压强度为
fcc内=fc+kfl
(21)
其中,k=(1+sinφ)/(1-sinφ),φ为混凝土的内摩擦角。
3.4 外方箍筋与外螺旋间区域Ⅲ强度计算
矩形箍筋提供的约束为非均匀围压力,故较难计算实际围压力大小。Saatcioglu和Razvi[15]提出采用等效约束应力fle来代替实际约束应力,如图6所示。
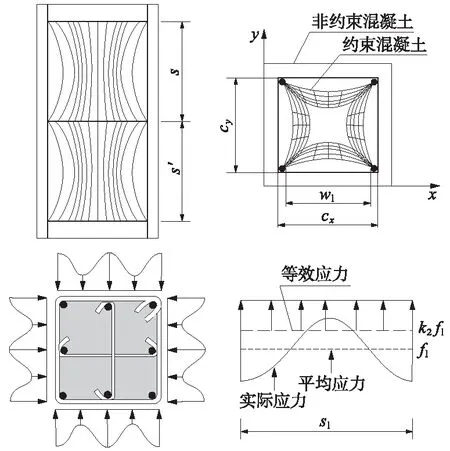
图6 矩形箍筋等效约束应力
Cusson和Paultre[16]给出了矩形箍筋约束核心混凝土区域的等效侧向约束力为
(22)
式中,fle为等效约束应力;fs,c为约束混凝土达峰值时箍筋应力;s为箍筋间距;cx为x方向边缘箍筋中轴线之间的距离;cy为y方向边缘箍筋中轴线之间的距离;Ashx和Ashy分别为x和y方向箍筋的横截面总面积;ke为等效约束系数,其表达式为
(23)
式中,wi为相邻纵筋间的第i个横向净距;s′为箍筋间净距;ρc为纵筋的配筋率。
故根据Saatcioglu理论,可计算该区域约束混凝土抗压强度为
fcc方=fco+k1fle
(24)
k1=6.7(fle)-0.17
(25)
式(24)和式(22)中,fs,c取箍筋屈服强度fyv。当为高强箍筋约束高强混凝土时,由于混凝土强度较大并且处于多重围压下,极限状态时混凝土横向变形相对较小,箍筋可能未达到屈服强度,故导致计算值可能偏高。此时可采用迭代法计算箍筋应力。
文献[17]表明,高强箍筋约束高强混凝土的峰值强度、峰值应变的计算公式分别为
(26)

(27)
式中,fcc、fco、εcc、εco分别为约束与非约束混凝土的峰值强度、峰值应变。
Nielsen等[18]研究表明,对于强度范围在40~110 MPa的混凝土,三轴受压时混凝土达到峰值应力所对应的侧向应变ε3,p和轴向应变εcc之间的关系为
εcc=-2.2ε3,p
(28)
极限状态时箍筋应力计算的迭代过程如下。
(1)首先假定箍筋极限应力fs,c=fyv,代入式(22)计算fle;
(2)通过式(27)和式(28),估算混凝土侧向应变ε3,p;
(3)假定箍筋应变等于ε3,p,利用箍筋的本构关系计算应力fs,c=Es×ε3,p;
(4)若fs,c (5)重复(2)~(4)步骤,直至fs,c值收敛。 通过上述分析,将各区域的计算强度叠加,即得外方内双螺旋箍筋约束混凝土柱的轴压承载力计算公式 Nu=A1fcc+(A2-A1)fcc外+(A3-A2)fcc方+fyAs (29) 若考虑可靠度、长细比和各区域强度叠加时峰值荷载不同步的影响,分别添加各影响系数得该新型约束结构柱轴压承载力计算公式为 Nu=0.9η[A1fcc+(A2-A1)fcc外+ (A3-A2)fcc方+fyAs] (30) 式中,0.9为考虑可靠度调整系数;φ为考虑长细比影响的承载力折减系数,取值见《混凝土结构设计规范》[12];A1、A2、A3分别为内圆包围的面积、外圆包围的面积、矩形包围的面积;η为考虑采用叠加原理时,各元件达峰值荷载不同步而引入的叠加折减系数[19],可取为0.9,如图7所示。 为验证以上推导的理论计算模型,设计了3根多重螺旋箍筋约束混凝土柱与1根普通单层箍筋混凝土柱构件。其中试件RC为普通混凝土方柱,试件DRC为多重螺旋箍筋约束混凝土方柱。螺旋箍筋间距和外方箍筋间距均取值为60 mm,保护层厚度为20 mm。具体试件参数如表1和图8所示。本文给出了混凝土柱DRC2-C50的详细计算过程,相关计算参数如表2所示,其他柱试件采用相同的计算方法。 图7 荷载不同步引起的承载力折减 图8 轴压柱截面尺寸与配筋(单位:mm) 表1 试件设计参数 注:ρ为纵筋配筋率;ρv为箍筋体积配箍率。 表2 柱DRC2-C50的计算参数 注:fc为混凝土抗压强度;ft为混凝土抗拉强度;fyh为箍筋屈服强度;fyv为纵筋屈服强度;Ri,Ro分别为圆筒内外半径;dcor内为内螺旋有效直径,dcor外为外螺旋有效直径,Asp为箍筋截面面积,Azn为內芯纵筋截面面积,Azw为外芯纵筋截面面积,Aw为外围纵筋截面面积,A1、A2、A3分别为内圆包围的面积、外圆包围的面积、矩形箍筋包围的面积。 4.2.1 中间夹层筒体区域II强度值计算 内螺旋箍筋提供的约束力 外螺旋箍筋提供的约束力 筒体外围压 Po=ψflo=1.2×3.42=4.1 MPa 约束效用系数 s′=60-8=52 mm,ds=180 mm Azw总=6×50.24=301.44 mm2 故 混凝土筒体受到的有效侧围压为 fle=kePo=0.87×4.1=3.57 MPa 混凝土筒体区域Ⅱ的抗压强度为 4.2.2 内核芯区域I强度值计算 混凝土筒体对内核芯混凝土的围压 σz=fcc外=71.23 代入式(19)得 由于fl2=Pi,故可得内核芯混凝土的全围压为fl=fl1+fl2=7.58+9.88=17.46 MPa 则内核心区域Ⅰ混凝土抗压强度为 fcc内=fc+kfl=50+1.5×17.46=76.19 MPa 其中,k=(1+sinφ)/(1-sinφ),φ为混凝土的内摩擦角,其变化范围为30°~50°,由于受到外部结构较强的约束,侧压力较大,计算时理论值一般可取在k=1.5~3.0[20],此处取k=1.5。 4.2.3 外方箍筋与外螺旋间区域Ⅲ强度值计算 0.66 k1=6.7(fle)-0.17=6.96fcc方=fco+k1fle= 50+6.96×0.80=55.57 MPa 由以上计算结果,代入下式可得此约束混凝土柱的轴向承载力大小为 Nu=0.9η[A1fcc+(A2-A1)fcc外+(A3-A2)fcc方+ fyAs]=3 226.6kN 这里不考虑采用折减,以得到最大计算值。 4.2.4 无螺旋箍筋同尺寸混凝土柱承载力计算 经计算,无螺旋箍筋同尺寸混凝土柱承载力为 承载力提高值为 N′=3 226.6-2 620.2=606.4 kN 即相对于普通RC柱承载力提高约23.1%,说明该约束结构可有效提高混凝土柱的轴向承载能力。 通过有限元分析软件Abaqus,针对以上设计的轴压柱进行有限元模拟分析,以验证理论计算结果的有效性。 图9 钢筋骨架与混凝土柱模型 采用三维变形体实体单元和三维变形体线形单元分别对混凝土和钢筋进行建模,轴压柱上下两端添加厚度20 mm刚性盖板进行加载,以保证均匀受压。材料本构:钢筋采用二折线本构模型,混凝土采用考虑塑性损伤的CDP模型,CDP模型的参数计算采用了丁-余模型[21]给出的混凝土受压本构关系曲线。钢筋与混凝土之间采用嵌固粘结方式,并在盖板的上下端设置参考点,采用位移加载方式,并对上参考点施加轴向10 mm位移,对底端参考点施加固定约束。建立的模型如图9所示。 通过ABAQUS后处理模块,得出了各轴压柱的荷载位移曲线,如图10所示。从图10可以得出各柱的极限轴压承载力,并与理论计算值进行了对比,如表3所示。其中柱RC计算值较小,误差较大,可能是由于未考虑混凝土柱保护层强度贡献,而其他柱试件的误差较小,理论值与模拟分析值吻合良好。 图10 柱荷载-位移关系曲线 从图10可以看出,通过配置多重螺旋箍筋,柱DRC-C40的极限轴压承载力显著提高,曲线下降段更加平缓,延性得到改善。随着混凝土强度的增加,极限荷载相应提高,但延性性能有所下降。其中柱DRC-C50混凝土单元最大轴向主应力S33,数值为65.72 MPa,其他柱的混凝土最大轴向应力结果如表3所示,并与理论计算值进行了对比。从表3可以看出,核心混凝土最大轴向应力误差相对较大,且随着混凝土强度的提高而增大。当混凝土强度等级小于C50时,计算精度较好,误差较小。 当核心区混凝土达极限压应力状态时,各混凝土柱的钢筋应力如图11所示。从图11可看出,DRC-C40柱和DRC-C50柱钢筋均已屈服,而DRC-C60柱钢筋未屈服,外层方箍极限状态时的平均应力为287 MPa,与理论迭代计算值273 MPa基本吻合,证实了高强箍筋约束高强混凝土柱外方箍筋未屈服的基本理论假定。 表3 模拟计算值与理论值对比 图11 约束混凝土柱峰值荷载时的钢筋应力云图 (1)建立了外方内双螺旋箍筋约束混凝土柱轴压下的约束理论模型,以约束混凝土计算理论为基础,采用了叠加原理和统一强度理论,推导了该约束形式下混凝土柱的轴压承载力计算方法。 (2)基于有限元软件ABAQUS,对外方内双螺旋箍筋约束混凝土柱的轴压性能进行了数值模拟计算,并将模拟值与理论值进行了对比分析,结果表明理论值与模拟计算值吻合良好,且理论值偏于保守。 (3)对于该类新型约束混凝土柱,ABAQUS模拟获得的核心混凝土最大应力值与理论值存在一定误差,当混凝土强度和箍筋屈服强度较小时,误差较小。采用高强箍筋和高强混凝土约束该类新型混凝土柱的理论研究,还需进一步深化。 (4)理论分析结果显示,多重约束混凝土的承载性能明显优于普通箍筋约束混凝土柱的承载性能。3.5 轴压承载力计算
4 算例分析
4.1 构件基本设计尺寸与配筋

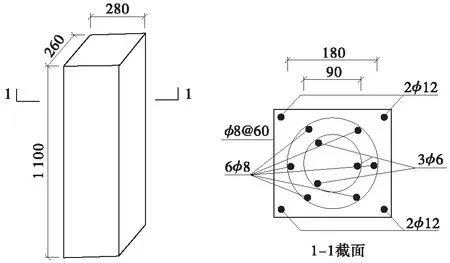


4.2 计算过程
5 有限元分析
5.1 模型的建立
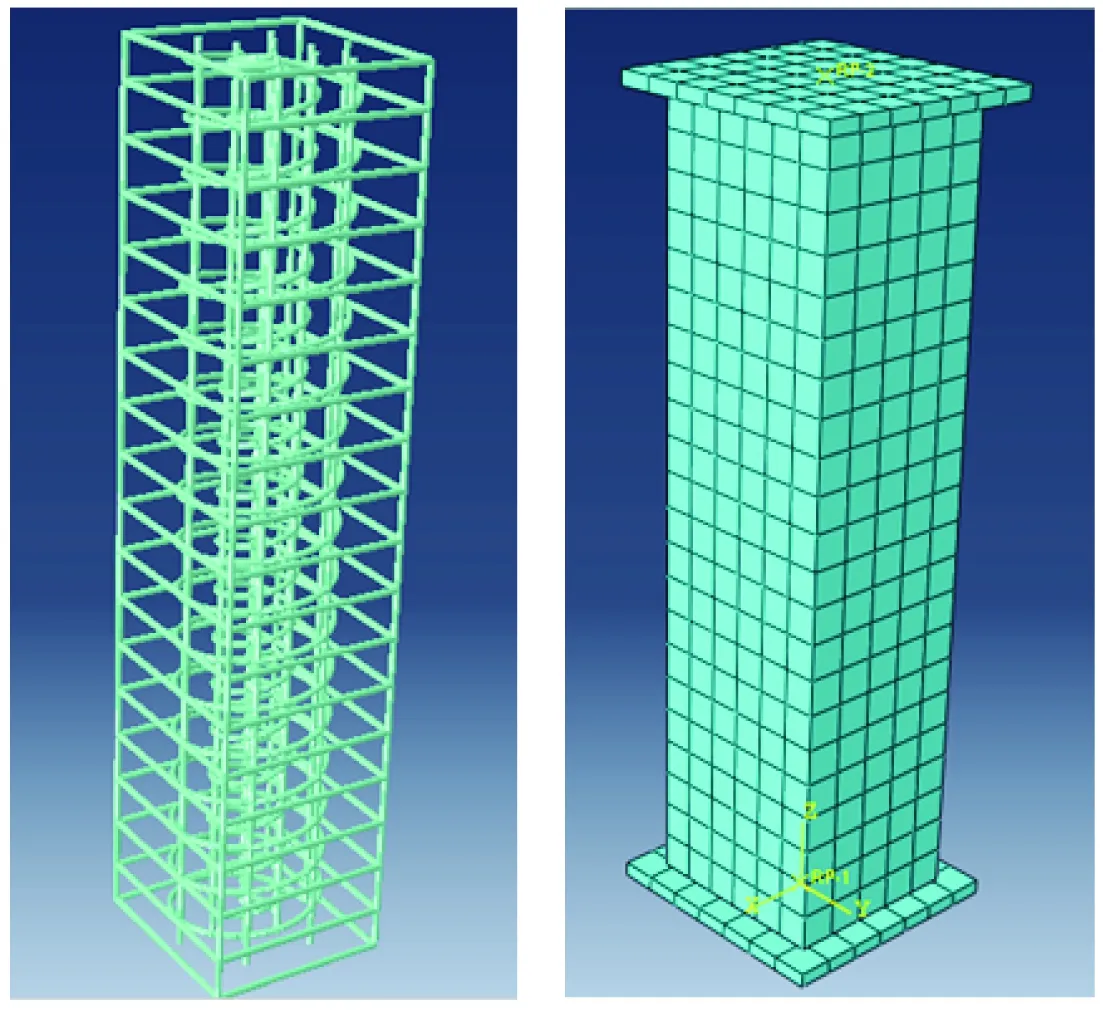
5.2 模拟结果与分析




6 结语

