动物种群中炭疽模型解的存在性与稳定性分析
周可可, 薛亚奎
(中北大学 理学院, 山西 太原 030051)
0 引 言
炭疽病是由炭疽杆菌引起的一种可人畜共患的急性传染病. 发病率最高的是牛羊, 猪也可发病, 人类会因屠宰、 食用或者与病死畜接触而受到感染. 这种疾病可以通过皮肤、 胃肠道或者口鼻吸入感染, 有可能是致命的. 炭疽病对社会公共卫生和经济发展的危害迄今仍然非常大. 最近几年世界多地出现了动物种群的炭疽大爆发, 引起了许多学者的关注和研究[1-9]. Saad-Roy等[10]建立了以Logistic增长并且考虑尸体腐烂的炭疽模型, 但是没有将炭疽疾病的潜伏时间纳入研究范围. 2010年, Lewerin等[11-12]通过观察发现在自然感染的情况下, 牛感染炭疽疾病的潜伏期在 1~14 d 之间. Mushayabasa等[13]研究了易感动物以常数输入并且考虑炭疽疾病具有潜伏期的模型, 但是在生态系统中资源有限, 考虑动物种群常数输入有一定的局限性. 本文将基于炭疽病传播的特征, 建立一类具有潜伏期且以Logistic增长的炭疽病模型, 确定炭疽疾病的流行条件, 研究和讨论模型中无病平衡点和地方病平衡点的稳定性, 并且通过数值模拟分析在地方病平衡点处系统的分支情况.
1 模型的建立
本文将模型划分为5个仓室:s为易感动物,e为潜伏期动物,i为受感染动物,a为环境感染,c为动物的尸体. 考虑到炭疽疾病主要为食草动物感染且炭疽病的易感性各不相同, 牛羊是最易感染的. 通常情况下, 牛羊等家畜在受到污染的土壤、 植物或者水中吞食炭疽孢子时会受到感染, 本文将考虑环境污染a对炭疽疾病传播的影响. 此外, 动物的尸体为有机物, 本文也将尸体的腐烂κ纳入考虑. 因此本文讨论了食草动物的生物动力学性态, 建立模型如下
(1)
系统(1)中的参数定义如表 1 所示.

表 1 系统(1)的参数定义
根据生态系统的实际意义, 所有参数均为正, 0<ρ<1, 这里假设r>μ, 表明动物种群将持续存在[10].
由于n=s+e+i, 可以用e,i,a,c,n代替s,e,i,a,c, 因此模型(1)变为
(2)
2 平衡点的存在性
由系统(2)的第5个方程得
所以
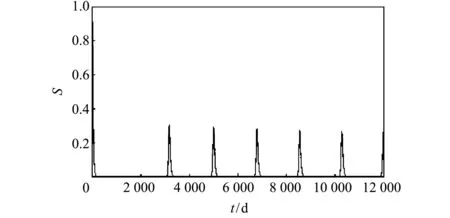
假设0 是系统(2)的正不变集. 下面在可行域Γ中研究系统的动力学性态. 显然系统(2)存在一个无病平衡点P0=(s0,0,0,0,0). 利用下一代矩阵法[14], 可以计算出系统(2)的基本再生数为 下面研究系统(2)的地方病平衡点. 易得系统(2)的地方病平衡点P*(n*,e*,i*,a*,c*), 其中 n*= 将其代入系统(2)的第5个方程可以得到一个关于c*的一元二次方程 F(c*)=A(c*)2+Bc*+C, 式中: B= (μ-r)(γ+μ+φ)+ηaβKγφ(μρ+φ)+ 2rακ(γ+μ+φ)(μ+φ))], 显然F(0)=C. 当R0>1时,C>0, 即系统(2) 存在唯一的正平衡点. 因此有如下定理. 定理1 当R0<1时, 系统(1)存在无病平衡点P0; 当R0>1时, 存在唯一的地方病平衡点P*. 定理2 当R0<1时, 无病平衡点P0在可行域Γ内局部渐近稳定; 当R0>1时, 无病平衡点P0在可行域Γ内不稳定. 证明系统(2)在P0=(s0,0,0,0)的Jacobian矩阵为 其中一个特征根为μ-r, 另外4个特征根为方程λ4+a1λ3+a2λ2+a3λ+a4=0的根. a1=γ+μ+φ+μ+α+κ, a2=(μ+φ)(γ+μ)+(α+κ)(μ+φ+γ+μ)+ ακ-βρηan, a3=(ακ-βρηan)(μ+φ+γ+μ)+(α+κ)(μ+φ)(γ+μ), 显然ai>0,i=1,…,4, 则有 H1=a1>0, H2=a1a2-a3=(μ+φ+γ+μ)[(μ+φ)(γ+μ)+(α+κ)(μ+φ+γ+μ)]+ (μ+φ)(γ+μ)(μ+φ+γ+μ)(μ+φ+γ+μ+α+κ)(α2+κ2+ακ+βρηan)+ [(μ+φ)3(α+κ)+(γ+μ)3(α+κ)+(μ+φ)2(α+κ)2+(μ+φ)(γ+μ)(α+κ)2+ H4=a4H3>0, (R0<1). 根据Routh-Hurwitz判据知, 定理2成立. 定理3 当R0<1时, 无病平衡点P0在可行域Γ内全局渐近稳定, 疾病会逐渐消亡; 当R0>1时, 无病平衡点P0在可行域Γ内不稳定. 证明将x=(e,c,i,a)T定义为受感染部分的向量, 考虑到Q=ωTV-1x,ωT>0是V-1F的左特征向量, 且V-1F为不可约的. 正如文献[15]中 此时 所以Q′=ωTV-1x′≤(R0-1)ωTx-ωTV-1f(x,y)≤(R0-1)ωTx. 因为f(x,y)≥0, 则R0<1时在可行域Γ内Q′≤0. 对于此系统而言,Q′是一个Lyapunov函数. 根据Lyapunov函数和LaSalle不变原理, 定理3成立. 定理4 当R0>1时, 地方病平衡点P*在可行域Γ内是局部渐近稳定的. 证明无病平衡点P0处的Jacobian矩阵为 系统的左特征向量为 则分支参数a,b分别为 依据文献[16]中定理4.1可知本文定理4成立. 图 1 为易感动物s的时间序列图, 图 2 为相同参数下系统(2)的相图. 从图 1 观察到, 随着时间的变化, 炭疽疾病在短时间内出现了大爆发, 随后系统出现周期振荡. 从图 2 观察到系统在地方病平衡点处发生Hopf分支, 出现极限环, 表明了地方病平衡点不稳定. 从而说明在这种情况下炭疽疾病呈现出周期性爆发. 图 1 系统(2)易感动物s的时间序列图Fig.1 A time series diagram of susceptible animals s in system (2) 图 2 系统(2)的相图Fig.2 The phase diagram of the system (2) 本文主要讨论了具有潜伏期的炭疽病模型, 且考虑易感动物以Logistic函数增长, 利用下一代矩阵法计算出模型中炭疽流行的基本再生数R0. 通过构造Lyapunov函数且利用LaSalle不变集原理证明了当基本再生数R0<1时, 无病平衡点P0全局渐近稳定; 当基本再生数R0>1时, 系统存在唯一的地方性平衡点P*, 且通过Routh-Hurwitz判据证明了该地方病平衡点P*局部渐近稳定, 同时通过数值模拟发现系统在地方病平衡点处发生Hopf分支, 出现极限环并存在周期解, 炭疽疾病发生周期性爆发.3 无病平衡点P0的稳定性
4 地方病平衡点P*的稳定性

5 数值模拟
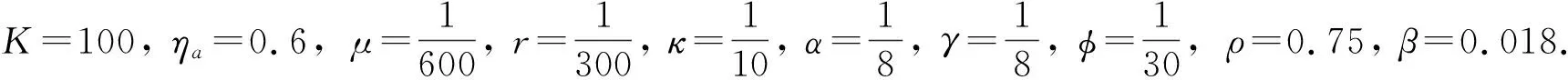

6 结 论

