具有Allee效应单种群反馈控制模型的动力学分析
方 侃,陈晓英
(福州大学至诚学院,福建福州350001)
单种群Logistic 模型是非常经典的生物数学模型,此前学者已证明该模型有唯一的正平衡点x*=1,该正平衡点是无条件局部渐近稳定和全局渐近稳定的.式(1)如下:

其中r是正数.
Allee效应描述的是一个密度依赖相关性,即个体适合度随着种群密度或大小的降低而降低的现象.当种群密度低于某一阙值的时候,生育率会低于死亡率,而使种群密度进一步缩小直到灭绝.近年来,众多学者都在研究生物数学模型加Allee 效应[1-8].其中单种群Logistic 模型加Allee 效应的动力学行为可以从文献[5]得到,即式(2)存在同样唯一的正平衡点x*=1也是全局渐近稳定的,说明Allee效应没有改变此系统的稳定性.式(2)如下:

其中r,β都是正数.
文献[4]研究了加Allee效应的Lotka-Vloterra捕食食饵模型,证明了虽然Allee效应没有改变此系统正平衡点的稳定性,但是花了更多的时间去达到这个平衡状态,并且Allee效应同时减少了捕食者和食饵在平衡状态的种群密度.式(3)如下:
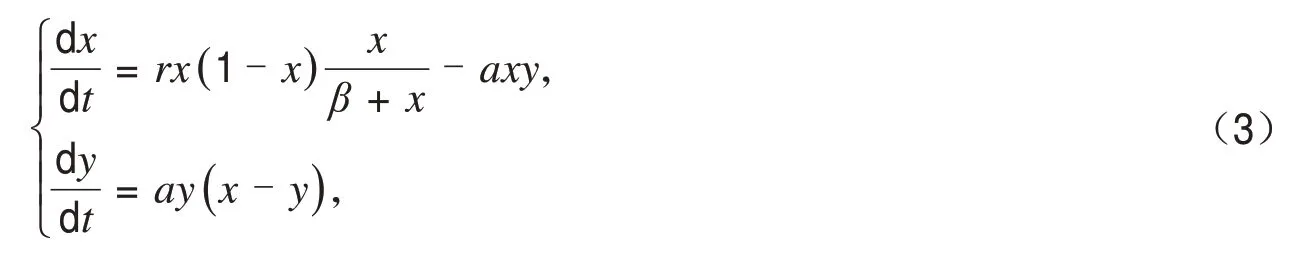
其中r,a,β都是正数.
反馈控制变量代表了人类的捕获[9],是导致种群数量减少的一个重要因素之一.文献[9]提出了单种群Logistic 模型加反馈控制的模型,得到的唯一正平衡点也是全局稳定的,
最终证明了反馈控制变量只是改变了平衡点的位置,没有影响单种群Logistic 模型的动力学行为.式(4)如下:

其中b,r,a,c都是正数.
文献[1]提出了单种群Logistic模型加Allee效应和反馈控制的新模型:
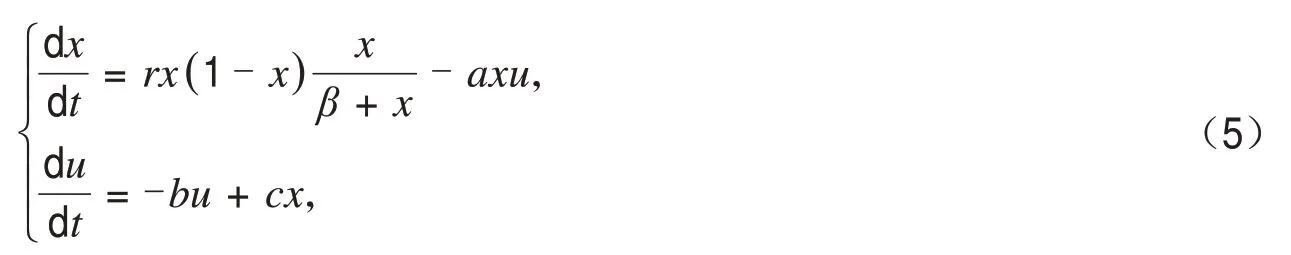
其中b,r,a,β,c都是正数.并讨论了这个模型的平衡点的存在性和局部稳定性.计算得出一个边界平衡A(0,0)和正平衡点B(x*,u*),其中(满足br-aβc>0时正平衡点存在.)
文献[1]在讨论边界平衡点A(0,0)的局部稳定的时候出现了计算错误,从而导致最后的局部稳定性结论出现错误,在本文第二部分的内容会进行更正.文献[1]中接着讨论了正平衡点B(x*,u*)的局部稳定性的条件,但没有讨论全局稳定性和可能产生的分支.将在第二部分讨论正平衡点B(x*,u*)的全局稳定性以及产生的分支.
1 局部和全局稳定性以及分支
1.1 A(0,0)的局部稳定性
引理1[2]假设平面系统已化为如下形式:

设O(0,0)是式(6)的孤立奇点,且P2(x,y),Q2(x,y)是O(0,0)的充分小邻域Sδ(O)内次数不低于2 的解析函数,于是存在函数Φ(x),满足:Φ(x)+Q2(x,Φ(x)) ≡0,|x|<δ,令ψ(x)=P2(x,Φ(x))=amxm+[x]m+1,其中am≠0,m≥2.于是有:
1)当m是奇数且am>0时,O(0,0)是不稳定结点.
2)当m是奇数且am<0时,O(0,0)是鞍点.
3)当m是偶数时,O(0,0)是鞍结点.另外当am>0(<0)时,抛物扇形落在右(左)半平面.
通过计算得到A(0,0)的雅克比矩阵如下:
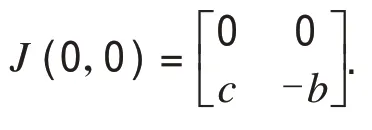
从而算得特征根λ1=0,λ2=-b<0.从而得到平衡点A(0,0)是非双曲的,若想进一步判断它的稳定性,需要做一个线性变换,文献[1]中由于线性变换代入方程计算错误,得到的结论是平衡点A(0,0)是一个
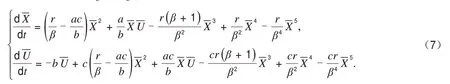
再做一个时间变换dτ=-bdt,式(7)变成式(8):
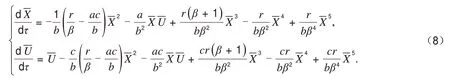

因此,根据引理1,得到如下结论:
定理11)若则边界平衡点A(0,0)是一个鞍结点.此时鞍点部分落在第一象限,而且式(5)存在正平衡点.
1.2 正平衡点B(x*,u*)的全局渐近稳定性
由于边界平衡点A(0,0)在br-aβc=0 时是稳定的,但此时式(5)不存在正平衡点,而A(0,0)在br-aβc≠0 是不稳定的,但是存在正平衡点,因此接下来进一步探讨正平衡点B(x*,u*)存在,即br-aβc>0时的全局渐近稳定性.
定理2如果满足以下3个条件:
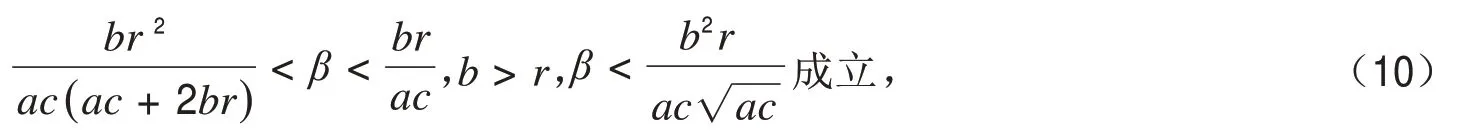
则正平衡点B(x*,u*)是全局渐近稳定的.其中
证明令f(x,u)=rx(1-x)-axu,g(x,u)=-bu+cx.考虑构造Dulac函数:u*(x,u)=代入计算可得,
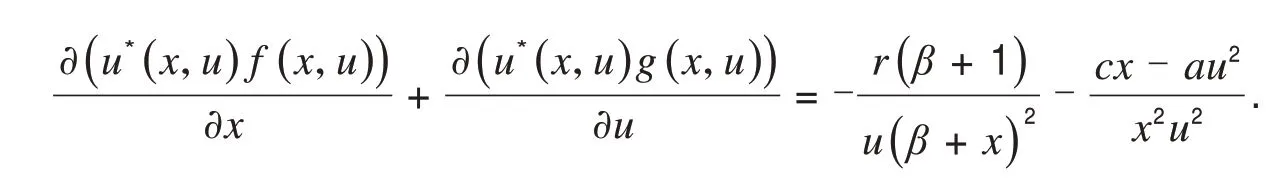

由式(10)及β>可得b2r2-2abcrβ
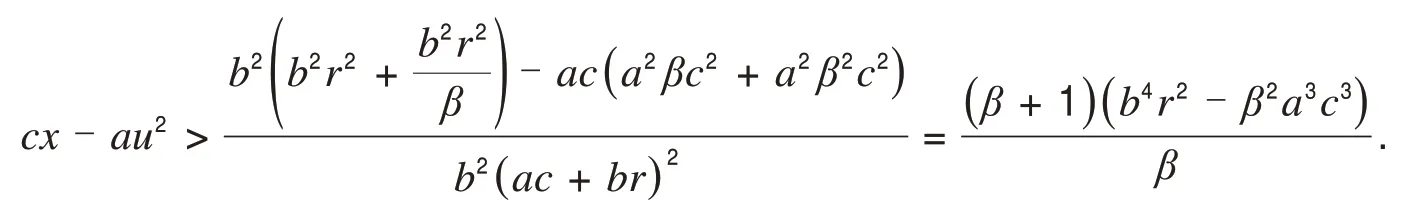
因此根据Dulac定理[3],在第一象限不存在极限环,也就证明了正平衡点B(x*,u*) 是全局渐近稳定的.
1.3 Hopf分支
本节讨论正平衡点B(x*,u*) 附近的Hopf分支.为了简化计算,先对式(5)做一个线性变换如下:
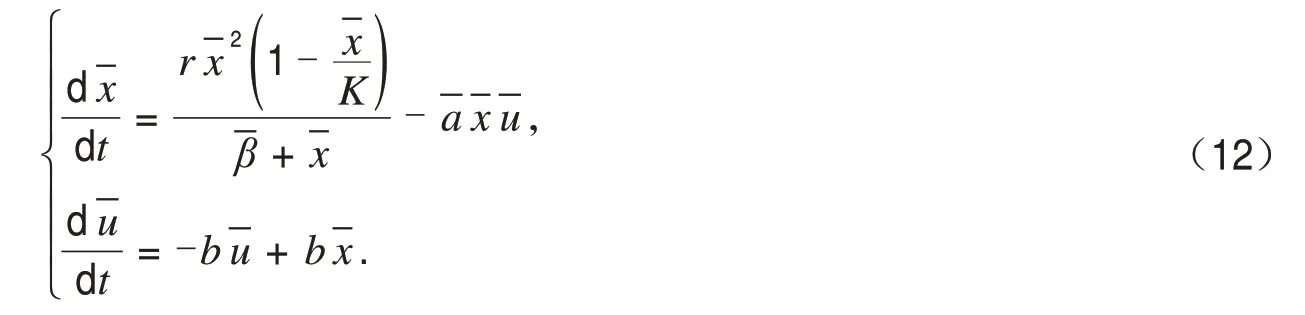
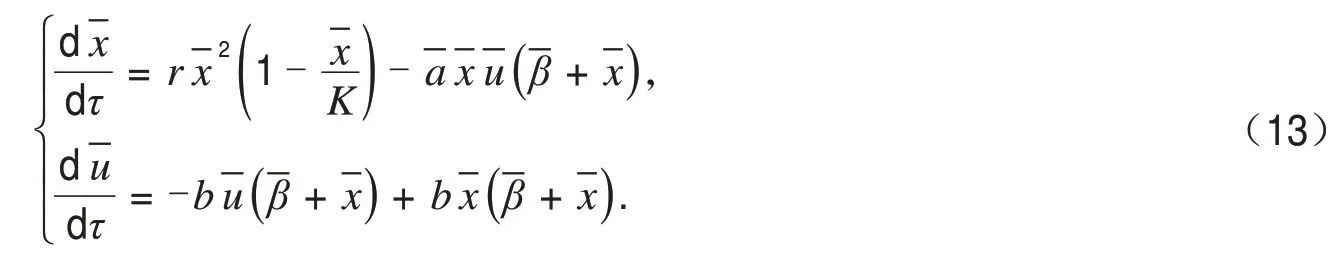

由于式(14)等价于式(5),则有

定义b*=,可以得到以下结论.
定理3已知r>0,>0,K>1,则
1)如果b>b*,则正平衡点(1,1)是一个源;
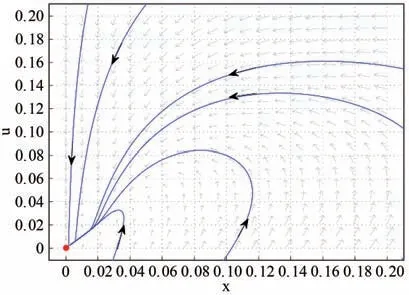
2)如果b 3)如果b=b*,则(1,1)是一个细焦点或者是一个中心. 证明正平衡点(1,1)对应的雅克比矩阵如下: 取参数b,考虑当b=b*时,Hopf分支的存在性.因为,从而综上所述满足三个条件:,因此式(13)在b=b*产生一个Hopf 分支,可以看到正平衡点(1,1)的稳定性随着参数b的改变而改变,当迹Tr的符号从负变为正的时候(1,1)的拓扑结构发生改变从而产生分支,因此在(1,1)附近至少存在一个极限环. 将在这一部分进行数值模拟来验证结果的正确性.先考虑式(5)的相图,如图1、图2所示. 图1 式(5)对应的相图Fig.1 Phase portrait 1 of system(5) 图2 式(5)对应的相图Fig.2 Phase portrait 2 of system(5) 图1取r=0.1,β=0.1,a=1,b=0.1,c=0.1 得到系统(5)对应的相图,此时可知边界平衡点A(0,0)是一个稳定的结点,此时系统不存在正平衡点,种群灭绝. 图2取r=0.2,β=0.1,a=1,b=0.1,c=0.1 得到式(5)对应的相图,此时系统存在正平衡点,由图可知边界平衡点A(0,0)在第一象限是鞍点部分. 再考虑与式(5)等价的式(13)的相图,如图3、图4所示. 图3 式(13)对应的相图Fig.3 Phase portrait 3 of system(13) 图4 式(13)对应的相图Fig.4 Phase portrait 4 of system(13) 图4取-β=0.1,K=50,b=0.012 9,r=0.1得到式(13)对应的相图,可知当取b=0.012 9<0.0133,扰动后式(13)就出现一个稳定的极限环,而平衡点的稳定性由稳定变为不稳定. 当单种群Logistic 模型同时加上反馈控制和Allee 效应,式(5)存在边界平衡点A(0,0),证明了这个平衡点在满足条件br-aβc=0时候是稳定的结点,此时式(5)不存在正平衡点,种群灭绝.而当br-aβc≠0时,A(0,0)是鞍结点,鞍点部分出现在第一象限.此时若满足br-aβc>0,则存在唯一正平衡点文献[1]证明了正平衡点的局部稳定性的条件,而本文继续讨论得到正平衡点的全局渐近稳定性的条件如下:并证明正平衡点附近发生Hopf分支,从而在正平衡点周围至少存在一个极限环. 综上所述,单种群Logistic 模型同时加上反馈控制和Allee 效应使得系统趋向不稳定了,由可知,种群密度随着Allee效应的增大而降低,从而会加速种群的灭绝.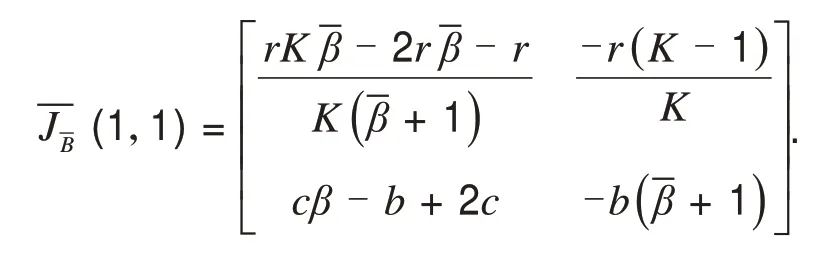
2 数值模拟



3 结论

