知识空间与简单拟阵的关系
杨桃丽,周银凤
(闽南师范大学数学与统计学院,福建漳州363000)
比利时数学心理学家Doignon 和美国数学心理学家Falmagne 于1985年首次提出了知识空间理论(Knowledge Space Theory,简称KST)[1],该理论是一种测试学习者认知水平的数学心理模型.
知识空间理论自提出到现在已经应用在自适应测评与辅助学习[2-3],ALEKS 系统的学习与评估等领域[4-5].该理论的提出受到了国内外学者的众多关注.1996年Rucsh等[6]研究了知识空间理论与形式概念分析之间的联系.Spoto等[7]将知识空间与形式概念分析联系起来,提出了由形式背景构造知识空间的方法.李进金等[8]通过对形式背景与知识基的联系进行研究,提出了由形式背景构造知识空间的另一种可行的方法.韩光明等[9]将布尔矩阵与知识空间相结合,研究了基于技能映射的知识空间的知识基,并给出了相关算法.周银凤等[10]基于技能与问题间的关系,研究了知识结构与技能背景间的联系.
知识基是知识空间理论的一个核心概念,在析取模型中它包含了知识空间的所有信息,从而由知识基可以张成一个知识空间.1993年Dowling[2]提出了由知识空间求知识基的方法.1999年受到该方法的启发,Doignon[11]给出了由知识基求知识空间的方法.2011年Falmagne 等[12]改进了Dowling 提出的方法并提高了求知识基的效率.
简单拟阵是组合数学中的一个重要分支,其发展至今已广泛应用于整数规划、网络流和电网络理论等领域[13].1976年Welsh[14]对简单拟阵与有限几何格进行研究,得到了两者之间的一一对应关系.赖虹建[15]提出了简单拟阵可由任意有限拟阵通过简单化的算法转化得到.毛华[16]研究了简单拟阵与概念格的关系,得到在同构意义下每个简单拟阵对应一个概念格的结论.
Wille 与李进金等都对知识空间与形式背景之间的关系进行了研究[6-8],而在同构意义下,简单拟阵与形式背景之间也存在着对应的关系.毛华[16]曾研究了简单拟阵与形式背景的相互构造.通过构造一种格结构,将知识空间与简单拟阵联系起来.
基于问题与技能之间的联系,首先给出求知识基的另一种方法.其次定义了问题与技能的伽罗瓦联络,讨论知识空间的伽罗瓦格与简单拟阵的几何格之间的关系.随后在讨论技能映射与拟阵的关系的基础上,通过构造一种格结构,进一步研究知识空间与简单拟阵之间的联系.最后得出了知识空间与简单拟阵是一一对应的结论.
1 预备知识
1.1 知识空间理论概述
知识状态是知识空间理论的基本概念之一.学习者在理想环境下能够正确回答问题域Q中的问题子集称为知识状态(knowledge state),记为K.显然K⊆Q.
定义1[12]设Q是非空问题集,K是由问题集Q的子集构成的知识状态集族,且K中至少包含∅和Q,称(Q,K)为知识结构(knowledge structure).在问题集Q明确的条件下,直接称K为知识结构.
定义2[12]若知识结构K满足并封闭,即对∀Ki,Kj∈K,有Ki∪Kj∈K,则称(Q,K)为知识空间(knowledge space),也可以称K为知识空间.
一般地,问题集Q是有限的,故本文所讨论的知识空间也是有限的.
定义3[12]设G,G′分别为两个集族,若G′是包含G中所有有限个元素的并所构成的集合,则称集族G'是G的张成(span),或称G张成G′.
显然,G′是关于并封闭的.在知识空间中,若存在一组非空子集族,这组子集族可通过并运算生成完整的知识空间,像这样的一组最小子集族,我们称之为知识空间的基(base).Falmagne 和Diognon 指出,知识空间是由它的基所确定的,在有限的知识空间中,有且仅有一个基与它对应[1].
定义4[12]设F为非空集族.对∀q∈∪F,F中包含q的极小集合称为q的原子(atom).若对∀q∈∪F,X是位于q的原子,那么称集合X∈F.
需要注意的是,空集不是原子.在有限的知识结构中,每个问题至少有一个原子,而所有问题的原子组成的集合是知识基.
定义5[12]设三元组(Q,S,τ)是一个技能映射,其中Q为非空问题集,S为非空技能集,τ是从Q到2S{∅}的映射.
技能和问题之间常见的联系有“或”和“与”关系,它们分别对应着两种模型,即析取模型和合取模型.析取模型表示为学习者仅需掌握与问题q的求解相关的某些技能便足以解决问题q;合取模型表示为学习者需掌握与问题q的求解相关的全部技能方能解决问题q.
在Falmagne 和Doignon 的研究中发现,技能映射通过析取模型诱导的知识结构必定为知识空间,通过合取模型诱导的知识结构为闭包空间[1].本文仅考虑技能映射的析取模型.
定义6[1]在析取模型下,技能子集T⊆S确定的知识状态为K={q∈Q|τ(q) ∩T≠∅}.当T取遍S中所有的子集(包括∅和S)时,可获得由技能映射(Q,S,τ)在析取模型下诱导的知识结构,记为K,且K满足并封闭,即K是一个知识空间.
例1设(Q,S,τ)是一个技能映射,其中Q={a,b,c,d},S={s,t,u},定义:τ(a)={t,u},τ(b)={s,t},τ(c)={u},τ(d)={s,u}.则该技能映射的Q−S表如表1所示.

表1 技能映射的Q−S表Tab.1 The Q−S table of skill mapping
因此,在析取模型下,每个技能子集T⊆S都可确定一个知识状态,所得到的这些知识状态包括∅和Q就组成了一个关于并封闭的知识空间,即
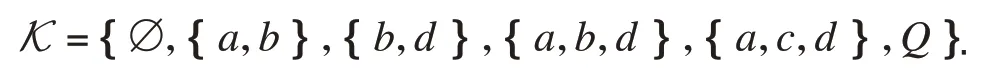
根据Dowling求知识基的方法[2],可得到知识空间K的知识基
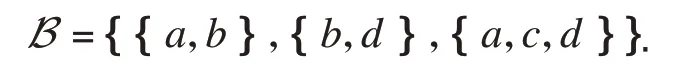
1.2 格论与拟阵的概述
在经典的拟阵论中,Welsh指出了有限几何格与有限简单拟阵的一一对应关系[14].引入格论与拟阵的一些定义和引理.
定义7[17]设X是非空问题集,≤是X上的二元关系,如果
1)自反性:x≤x,∀x∈X;
2)传递性:若x≤y,y≤z,则x≤z,∀x,y,z∈X;
3)反对称性:若x≤y,y≤x,则x=y,∀x,y∈X,
则称≤为X上的偏序关系,称(X,≤)为偏序集.在不导致冲突的情况下,也将偏序集简记为X.
定义8[17]设X是偏序集,若X的每个子集A都有上确界以及下确界,即∀A⊂X,supA与infA恒存在,则称X为完备格.
定义9[14]若对于∀x,y∈L,有:x和y覆盖x∧y⇒x∨y覆盖x和y,称格L是半模格.如果一个格是半模格并且每一元都是原子的并,则称它是几何格.
定义10[18]设X是一个集合,一个基B是X的一个子集族,用FB表示由B的并产生的族,即FB=称B是FB的一个生成元.显然,族FB是关于并封闭的.
定义11[18]在集合的包含关系下,FB是幂格2Q的一个并-子格.因此,完备格(FB,⊆)被称为FB的覆盖图.在B是由给定的技能映射确定的情况下,为简单起见,我们可以用F表示FB.
定义12[19]设E是一个有限集,F是由E的子集构成的集族,若满足以下条件:
1)∅∈F;
2)若X∈F且Y⊆X,则Y∈F;
3)若X,Y∈F且|X|<|Y|,则存在y∈YX,使X∪{y}∈F,则(E,F)称为拟阵(matroid),记为M=(E,F).
任意的X∈F是拟阵的独立集(independent set),非独立集的E的子集Y∈2EF称为拟阵的相关集(dependent set).这里的“独立”是线性无关概念的推广,而“相关”是线性相关概念的推广.
定义13[19]设M=(E,F)是一个拟阵,若{x}⊆E是M的相关集,则称x是拟阵M的环(loop).若x,y∈E不是M的环,但{x,y}是一个相关集,则称x,y是M的平行元素(parallel element),简称为M的平行元,或x平行于y.没有环和平行元的拟阵称为简单拟阵(simple matroid).
引理1[12]设(F,⊆)为一个几何格,(F,⊆)与定义在其原子集合上的拟阵之间是有限几何格族与简单拟阵族之间的一个双射.
注若几何格(F,⊆)有唯一的最小元和最大元,我们将用0代替∅表示该最小元,用1代替Q表示该最大元,则覆盖0的元且被1覆盖的元就称为原子,记为0 ≺B≺1.本节中所提到的原子即为(F,⊆)的原子.
2 问题与技能的伽罗瓦联络
我们知道在技能映射中有限的非空问题集与非空技能集是偏序集,并且它们在集合的包含关系下可以构成一个Galois 联络.给出求知识基的另一种方法,进一步讨论由该知识基张成的知识空间的伽罗瓦格与完备格(F,⊆)的同构关系.
在知识结构(Q,K)中,∀q1,q2∈Q,如果一个学习者能够正确解决问题q2,那么他一定能正确解决问题q1,即q1≤q2,称问题q1先于问题q2.则非空问题集Q是一个偏序集.
类似地,非空技能集S也是一个偏序集.下面给出问题与技能之间的伽罗瓦联络的定义.
定义14设(Q,S,τ)是一个技能映射,(Q,≤)和(S,≤)是偏序集,f∶Q→S与g∶S→Q是映射,如果f,g满足:∀q∈Q,∀s∈S,有s≤f(q) ⇔q≤g(s),则称(f,g)是Q与S之间的Galois 联络,简称(f,g)是(Q,S)的Galois联络.
例2设(Q,S,τ)是一个技能映射,其中Q={a,b,c,d},S={s,t,u,v},定义:τ(a)={t,u},τ(b)={s,u},τ(c)={s,v},τ(d)={t,v}.对∀M⊆Q,∀T⊆S,令f(M)={x∈S|∀q∈M,x∈τ(q)},g(T)={q∈Q|∀x∈T,x∈τ(q)}.
若M={b,c},T={u,v},则f(M)={s,u,v},g(T)={a,b,c,d}.从而
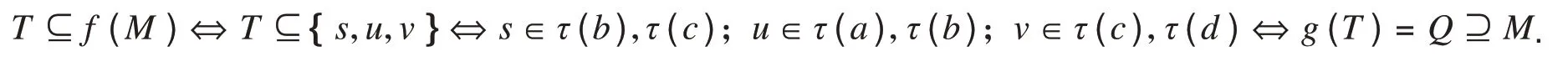
Gal(K)表示为S→Q的所有伽罗瓦联络形成的集合.在集合的包含关系下,Gal(K)是一个偏序集,其中K是有最小元∅并且满足并封闭的知识空间,从而是一个完备格.
定义15设K 是由技能映射(Q,S,τ)诱导的知识空间.对于偏序集(Q,≤),∀s∈S,定义↓s={q∈Q|s∉τ(q)}.于是可得如下结论.
定理1设(Q,S,τ)是技能映射,则由该技能映射确定的知识基为B={Q↓s|∀s∈S}.
证明在技能映射(Q,S,τ)中,对∀s∈S,∃q∈Q,使得s∉τ(q)成立,于是Q↓s∈B.另一方面,对∀q∈Q,∃s∈S,使得s∉τ(q)成立,于是问题q处的原子均可表示为Q↓s,从而(Q,S,τ)确定的基为B={Q↓s|∀s∈S}.
由定义15与定理1可知,在给定技能映射的情况下,可以快速求出知识基.
定理2令技能映射(Q,S,τ)确定的知识空间K是偏序集,B为知识基,(F,⊆)是完备格.定义映射f∶F→Gal(K)是一个双射(f与f−1保序),那么(F,⊆) ≅Gal(K).
证明下证∀A⊆F,f(A)的上、下确界存在.∀A⊆F,由(F,⊆)是完备格知,supA∈F.又由f为双射知,f(supA) ∈Gal(K),f(supA)≥f(a)(∀a∈A),故f(supA)是{f(a)|a∈A}的上界.设b∈f(Gal(K))是f(A)的上界,由f是双射知,∃a∈F,使得∀x∈A,b=f(a)≥f(x),则由f−1保序知,∀x∈A,a=f−1(b)≥x,故a≥supA.再由f保序知,f(a)≥f(supA),即b≥f(supA),从而f(supA)是f(A)的上确界,即f(supA)=supf(A).同理可证∀A⊆F,f(A)的下确界存在.从而可得(F,⊆) ≅Gal(K).
例3在例1中,知识空间K={∅,{a,b},{b,d},{a,b,d},{a,c,d},Q} ,它的基B={{a,b},{b,d},{a,c,d}},F是B的张成.若A={{a,b},{a,b,d}},supA={a,b,d}∈F,有f({a,b,d})={a,b,d}∈Gal(K),从而f是(F,⊆)与Gal(K)之间的同构映射.
3 简单拟阵与知识空间
知识空间与形式背景之间具有相互转换的关系,而在形式背景的伽罗瓦格与几何格同构意义下,简单拟阵与形式背景之间也存在着对应的关系.这时(F,⊆)中所有原子的集合指的就是知识基B.基于此,讨论技能映射与拟阵的关系,通过构造一种格结构,进一步研究知识空间与简单拟阵之间的联系.
3.1 由简单拟阵构造知识空间
对技能映射与拟阵之间的关系进行讨论,当拟阵中的有限集和闭集族被与技能映射有关的一些元所取代时,仍具有拟阵中的一些性质.于是有以下结论.
定理3设(Q,S,τ)是一个技能映射.M=(E,F)是一个拟阵,其中E是非空问题集Q的子集族,F是由E的并构成的集族,则满足以下性质:
1)∅∈F;
2)若E1∈F且E2⊆E1,则E2∈F;
3)若E1,E2∈F且|E1|<|E2|,则存在q∈E2E1,使E1∪{q}∈F.
证明由定义10知,F=
1)由于∅满足|∅|=0,于是∅∈F.
2)对∀E1,E2⊆Q且E2⊆E1,若E1∈F,则E2∈F.
3)对∀E1,E2⊆Q,令E1,E2∈F且|E1|<|E2|,若对∀q∈E2E1,均有E1∪{q}∈F.从而3)成立.
特别地,当M=(E,F)是简单拟阵时,E是知识基B,F是由B张成的集族,记为M=(B,F).
根据定理3中技能映射与拟阵的关系,可进一步研究知识空间与简单拟阵的关系.
定义16设K1,K2是两个知识空间.若存在双射f∶Q1→Q2满足:对于∀K⊆Q1,有K∈K1⇔f(K) ∈K2,则称K1同构于K2,记为K1≅K2.
将此处的两个知识空间同构视为同一结构.两个技能映射诱导的知识空间同构,它们的伽罗瓦格也是同构的.
定理4设M=(B,F)是一个简单拟阵,其中B是由技能映射(Q,S,τ)确定的知识基,F是B的张成.存在一个知识空间K满足Gal(K) ≅(F,⊆).即在同构意义下,一个简单拟阵M可唯一确定一个知识空间K.
证明由引理1知,(F,⊆)是一个几何格.设M=(B,F)是一个简单拟阵,(Q,S,τ)是一个技能映射,由定理2 可知,存在知识空间K满足Gal(K) ≅(F,⊆).因为知识空间K的伽罗瓦格与几何格同构,而B既是F的张成又为K的张成,从而简单拟阵M可唯一确定一个知识空间K.
例4设M=(B,F)是一个简单拟阵.设(Q,S,τ)是一个技能映射,其中Q={a,b,c,d},S={s,t,u,v},定义:τ(a)={s,v},τ(b)={t,v},τ(c)={u,v},τ(d)={t,u},可作出技能映射的Q−S表,如表2所示.

表2 技能映射的Q−S表Tab.2 The Q−S table for skill mapping
可求得知识基B={Q↓s|∀s∈S}={{a},{b,d},{c,d}}.由B张成的F={0,{a},{b,d},{c,d},{a,b,c},{a,b,d},{a,c,d},{b,c,d},1}=K,所以Gal(K) ≅(F,⊆).图1表示格(F,⊆)的示意图,在伽罗瓦格与几何格同构的意义下,该图也表示为知识空间的伽罗瓦格Gal(K)的示意图.
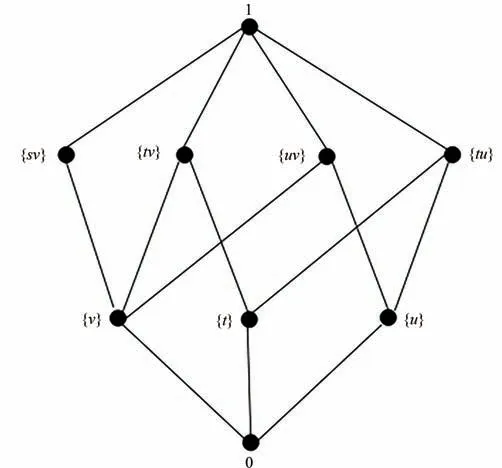
图1 格(F,⊆)Fig.1 L(F,⊆)
推论1设M1=(B1,F1),M2=(B2,F2)为两个简单拟阵.若M1≅M2,则KM1≅KM2.
证明若M1≅M2,由引理1 知(F1,⊆)和(F2,⊆)均为几何格,则有(F1,⊆) ≅(F2,⊆).又由定理2得Gal(KM1)≅(F1,⊆),Gal(KM2)≅(F2,⊆),故Gal(KM1)≅Gal(KM2),即KM1≅KM2.
例4中,在同构的意义下,得到了由简单拟阵构造的知识空间.接下来,将考虑定理4的逆命题是否成立.也就是说,在什么情况下,一个知识空间可以建立一个简单拟阵.
3.2 由知识空间建立简单拟阵
毛华在研究拟阵与概念格的关系时,得到了任意几何格是完备格,但任意完备格不一定是几何格的结果[20].引理2将是判断完备格是不是几何格的关键.
引理2[16]设B是知识空间K的基.若B满足以下条件,则(F,⊆)是一个几何格.
1)(F,⊆)是原子格,即B1,B2∈B⇒B1⊄B2.
2)(F,⊆) 是半模格,令{B1,…,Bg}⊆B,并 且{Bt1,…,Btn},{Bs1,…,Bsm}∈B{}B1,…,Bg.设F=B1∪…∪Bg满足:
对于∀B∈B{B1,…,Bg},有F∪B≠F,F1=F∪Bt1=…=F∪Btn,满足:对∀B∈B{}
B1,…,Bg,Bt1,…,Btn有F1≠F∪B,并且对∀B∈B{B1,…,Bg,Bs1,…,Bsm},有F2=F∪Bs1=…=F∪Bsm满足F2≠F∪B.
若F1≠F2.则对∀B∈B{B1,…,Bg,Bt1,…,Btn,Bs1,…Bsm},有F1∪F2∪B≠F1∪F2.
结合定义9与定义11可知(F,⊆)是一个几何格.
定理5设K1,K2是两个知识空间,K1,K2的基分别为B1和B2,且它们满足引理2 的条件1)和2).若K1≅K2,在同构意义下,有(B1,F1)≅(B2,F2),即在同构意义下,一个知识空间K确定唯一一个简单拟阵(B,F).
证明设M1=(B1,F1),M2=(B2,F2)为两个简单拟阵.若K1≅K2,则由定义16有Gal(K1)≅Gal(K2).因为知识基B1和B2满足引理2 的条件1)和2),所以(F1,⊆),(F2,⊆) 都是几何格.又由定理2,Gal(K)≅(F,⊆)得Gal(K1)≅(F1,⊆),Gal(K2)≅(F2,⊆).故(F1,⊆)≅(F2,⊆),从而(B1,F1)≅(B2,F2).
例5设K是由(Q,S,τ)确定的知识空间,B为知识空间K的基,其中Q={a,b,c,d,e},S={s,t,u},定义:τ(a)={s},τ(b)={s,t},τ(c)={s,u},τ(d)={t},τ(e)={u},技能映射的Q−S表如表3所示.

表3 技能映射的Q−S表Tab.3 The Q−S table for skill mapping
可得到K的基B为{{a,b,c},{b,d},{c,e}},其中B1={a,b,c},B2={b,d},B3={c,e}.在(F,⊆)中 ,必有 0 ≺Bi(i=1,2,3).易得B1∪B2={a,b,c,d},B1∪B3={a,b,c,e},B2∪B3={b,c,d,e},B1∪B2∪B3=Q.综上可知,B满足引理2的条件1)和2).
根据F的定义得,F={}0,Bi(i=1,2,3),Bi∪Bj(i≠j;i,j=1,2,3),B1∪B2∪B3.再由定理5 知,(B,F)是由知识空间K确定的简单拟阵,其中F是其闭集族.
推论2设M1=(E1,F1),M2=(B2,F2)为两个简单拟阵.若M1≅M2,则KM1≅KM2,BM1和BM2分别是KM1,KM2的基且满足引理2的条件1)和2),即(F1,⊆),(F2,⊆)均为几何格.
证明若M1≅M2,即(E1,F1)≅(E2,F2).因为BM1和BM2满足引理2 的条件1)和2),从而(F1,⊆) ≅(F2,⊆).由Gal(KM)≅(F,⊆)得Gal(KM1)≅Gal(KM2),故KM1≅KM2.
在伽罗瓦格与几何格同构的意义下,可以得到一个知识空间,并且它的基满足引理2 的条件1)和2),与定义在其基上的简单拟阵之间的对应关系.从而有下面的结论.
定理6设K是由技能映射(Q,S,τ)确定的知识空间.定义双射f∶S→B,B是K的知识基且B满足引理2的条件1)和2),MK为B上的简单拟阵.在同构意义下,则K→MK为一个双射.
证明由定理2、定理4和定理5即证.
例6例5 中知识基B={}{a,b,c},{b,d},{c,e},S={s,t,u},定义双射f∶S→B,则有f(s)={a,b,c},f(t)={b,d},f(u)={c,e}.B满足引理2的条件1)和2),从而(F,⊆)是一个几何格.又由知识基B张成的知识空间K={}∅,{b,d},{c,e},{a,b,c},{a,b,c,d},{a,b,c,e},{b,c,d,e},Q=F,即K与F是同一结构.故K→MK是一个双射.
根据引理2 的条件1)和2)可以快速判断(F,⊆)的几何性,在同构意义下,使由知识空间建立简单拟阵成为现实.
4 结束语
基于技能映射中的技能与问题之间的联系,主要探讨了知识空间与简单拟阵的关系.首先给出求知识基的另一种方法,该方法在一定程度上降低了计算知识基的时间复杂度,可快速地求出知识基.其次定义了问题与技能的伽罗瓦联络,讨论由知识基张成的知识空间的伽罗瓦格与几何格的同构关系.然后讨论技能映射与拟阵的关系,在伽罗瓦格与几何格同构的意义下,对知识空间与简单拟阵之间的关系进行研究.最后得出了知识空间与简单拟阵的一一对应关系.因此,研究知识空间与简单拟阵的关系是可行的.主要针对技能映射的析取模型进行研究,在以后的研究中,进一步挖掘知识空间与简单拟阵的关系,进一步考虑将技能映射的其他模型用于研究知识空间与简单拟阵的关系中.

