双曲线考点扫描

■河南省郑州市第一中学 武赫扬

双曲线是圆锥曲线中的三种曲线之一,也是高考考查的重点,主要考查定义、标准方程、几何性质等基础知识,考查基本技能与基本方法的运用。

一、知识扫描

双曲线的定义:在平面内到两定点F1,F2的距离的差的绝对值等于常数(小于F1F2|且大于零)的点的轨迹(或集合)叫作双曲线。定点F1,F2叫作双曲线的焦点,两焦点间的距离叫作焦距。

①当a＜c时,P点的轨迹是双曲线;

②当a=c时,P点的轨迹是两条射线;

③当a＞c时,P点不存在。

双曲线的离心率大于1,而椭圆的离心率e∈(0,1)。

双曲线的标准方程和几何性质如表1所示。

二、常见题型

考点一:双曲线的定义与标准方程

例1若实数k满足0＜k＜9,则曲线的( )。

A.焦距相等 B.实半轴长相等

C.虚半轴长相等 D.离心率相等

解析:因为0＜k＜9,所以9-k＞0,25-k＞0。

所以均表示焦点在x轴上的双曲线。

又25+(9-k)=34-k=(25-k)+9,所以它们的焦距相等,故选A。

表1

例2已知F为双曲线的左焦点,P,Q为C上的点。若P Q的长等于实轴长的2倍,点A(5,0)在线段P Q上,则△P Q F的周长为____。

解析:依题意知|P Q|=4a=12＞2a。

又因为A(5,0)在线段P Q上,所以P Q在双曲线的右支上。

可得|P F|-|P A|=2a=6,|Q F|-|Q A|=2a=6。

所以|P F|+|Q F|=24。

所以△P Q F的周长是|P F|+|Q F|+|P Q|=24+12=36。

点评:在应用双曲线定义时,要注意定义中的条件,搞清所求轨迹是双曲线,还是双曲线的一支。若是双曲线的一支,则需确定是哪一支。

例3已知双曲线的中心在原点,一个焦点为,点P在双曲线上,且线段P F1的中点坐标为(0,2),则此双曲线的方程是( )。

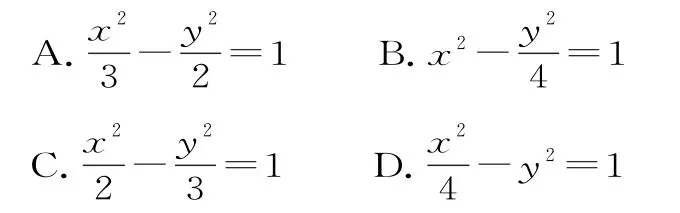
解析:设双曲线的标准方程为1(a＞0,b＞0)。

由P F1的中点为(0,2)知,P F2⊥x轴,,所以

所以5-a2=4a,所以a=1,b=2,所以双曲线方程为,故选B。

点评:确定双曲线的标准方程也需要一个“定位”条件,两个“定量”条件,“定位”是指确定焦点在哪条坐标轴上,“定量”是指确定a,b的值,常用待定系数法。若双曲线的焦点不能确定时,可设其方程为A x2+b y2=1(A B＜0)。若已知渐近线方程为m x+n y=0,则双曲线方程可设为m2x2-n2y2=λ(λ≠0)。

考点二:双曲线的离心率

例4已知F1,F2是双曲线E:=1的左,右焦点,点M在E上,MF1与x轴垂直,,则E的离心率为( )。

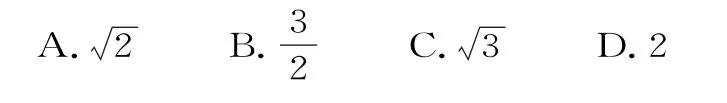
解析:因为MF1垂直于x轴,所以

点评:应区分双曲线中a,b,c的关系与椭圆中a,b,c的关系,在椭圆中a2=b2+c2,而在双曲线中c2=a2+b2。双曲线的离心率e∈(1,+∞),而椭圆的离心率e∈(0,1)。

例5过双曲线0)的右焦点F作一条直线,当直线倾斜角为时,直线与双曲线左、右两支各有一个交点;当直线倾斜角为时,直线与双曲线右支有两个不同的交点。则双曲线离心率的取值范围为( )。

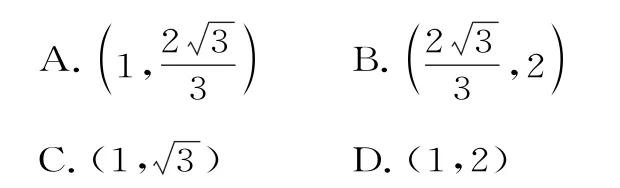
解析:由题意得,当直线倾斜角为时,直线与双曲线左、右两支各有一个交点,所以又当直线倾斜角为时,直线与双曲线右支有两个不同的交点,所以,所以此

点评:离心率是圆锥曲线的重要几何性质,是高考重点考查的一个知识点。这类问题一般有两类:一类是根据一定的条件求椭圆或双曲线的离心率;另一类是根据一定的条件求离心率的取值范围。无论是哪类问题,其解题关键都是建立关于a,b,c的关系式(等式或不等式),并且最后要把其中的b用a,c表达,转化为关于离心率e的关系式。

考点三:双曲线的渐近线

例6在平面直角坐标系中,已知双曲线的中心在原点,焦点在x轴上,实轴长为8,离心率为,则它的渐近线的方程为( )。

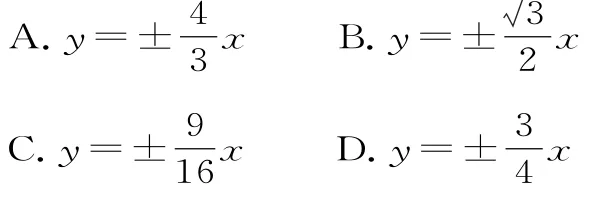
解析:由题意知渐近线的方程为y=

考点四:焦点三角形

例7点P在双曲线0,b＞0)上,F1、F2分别是双曲线的左、右焦点,∠F1P F2=90°,且△F1P F2的三条边长之比为3∶4∶5。则双曲线的渐近线方程是( )。

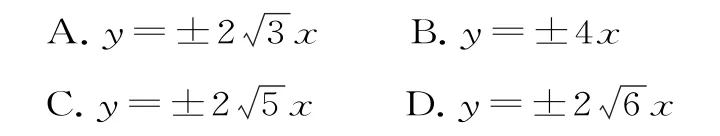
解析:设△F1P F2的三条边长为|P F1|=3m,|P F2|=4m,|F1F2|=5m,m＞0。

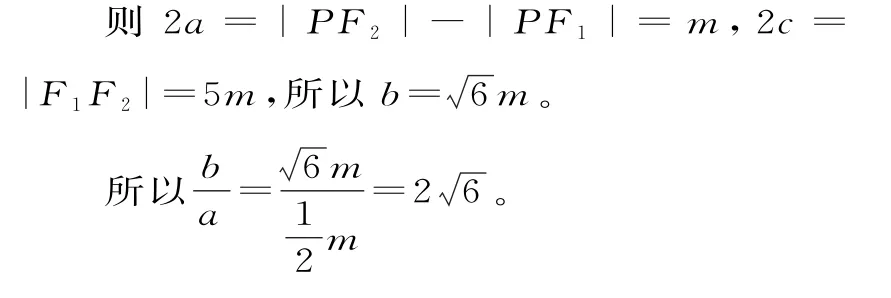
所以双曲线的渐近线方程是y=±26x。

故选D。

点评:用双曲线定义及虚轴长布列方程组即可求出双曲线的标准方程。在“焦点三角形”中,经常用到正弦定理、余弦定理、双曲线的定义。另外,还经常结合||P F1|-|P F2||=2a,运用平方的方法,建立它与|P F1||P F2|的联系。

例8设双曲线的左、右焦点分别为F1,F2。若点P在双曲线上,且△F1P F2为锐角三角形,则|P F1|+|P F2|的取值范围是____。

解析:由已知得则,设P(x,y)是双曲线上任一点。

由对称性不妨设P在右支上,则1＜x＜2,|P F1|=2x+1,|P F2|=2x-1。

因为∠F1P F2为锐角,则|P F1|2+|P F2|2＞|F1F2|2,即(2x+1)2+(2x-1)2

点评:先由对称性可设点P在右支上,进而可得|P F1|和|P F2|,再由△F1P F2为锐角三角形可得|P F1|2+|P F2|2＞|F1F2|2,进而可得x的不等式,解不等式可得|P F1|+|P F2|的取值范围。