R3中一类齐次Moran集的Hausdorff维数

党云贵， 刘彦芝， 王亮亮

吕梁学院数学系，山西 吕梁 033000

1 问题的提出

分形几何中Hausdorff 测度和维数是表征分形集的重要参量，也是研究分形集首要解决的问题；可是维数与测度的计算往往是十分困难的，只有少数的分形集得到了它们的 Hausdorff 维数及其测度的准确值[1～3].Moran集作为分形集中一类典型的集合，它的 Hausdorff 维数、填充维数、盒维数一直备受关注.现已研究出：一维空间中齐次 Moran 集的 Hausdorff 维数和 Packing 维数[4,5]，对R中一类广义非均匀 Cantor 集的Hausdorff 测度也得到值的估计[6]；人们将一维空间中Cantor集的构造方法推广到R2空间，得出R2中一类齐次 Moran 集的 Hausdorff 维数[7,8]；本文将一维空间中Cantor集的构造方法推广到三维空间，得到R3中一类齐次 Moran 集，并计算出它们的Hausdorff 维数.

设J⊆R3为非空有界闭集， {nk}k≥1，{lk}k≥1为正整数序列，{ck}k≥1为正实数序列，其中nk≥2.

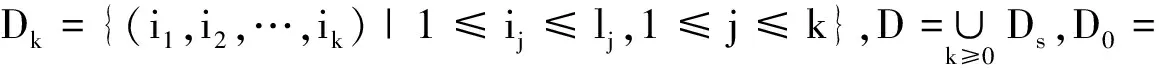
定义1R3中子集族{Iσ|σ∈D}称为具有齐次Moran结构，如果

(ii)对∀s≥0及σ∈Ds,Iσ*1,Iσ*2,…,Iσ*ls+1是Iσ的子集，并且对任意i≠j

int(Iσ*i)∩int(Iσ*j)=∅

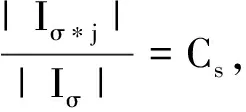
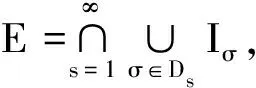
定义3 设E⊂R3,则E的s-容度为:Cs(E)={1/Is(μ)|μ是使得μ(E)=1的E上的质量分布}.

2 主要结果及其证明

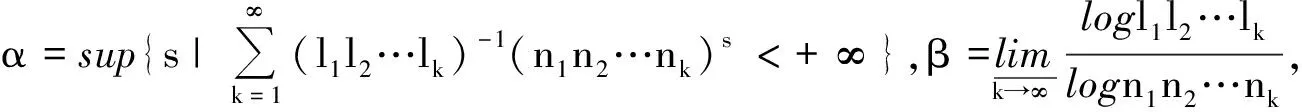
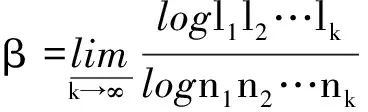
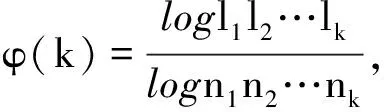
再证α=γ.

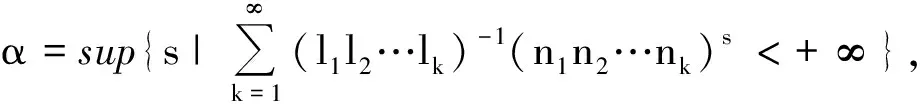
又(l1l2…lk)(n1n2…nk)-φ(k)=1，所以(l1l2…lk)(n1n2…nk)-(α-ε)≥(l1l2…lk)(n1n2…nk)-φ(k),则φ(k)≥α-ε，两边同时取下确界及ε的任意性，有γ≥α.

(l1l2…lk)-1(n1n2…nk)γ-2ε=(l1l2…lk)-1(n1n2…nk)γ-ε(n1n2…nk)-ε

≤(l1l2…lk)(n1n2…nk)-φ(k)(n1n2…nk)-ε≤(n1n2…nk)-ε≤2-kε

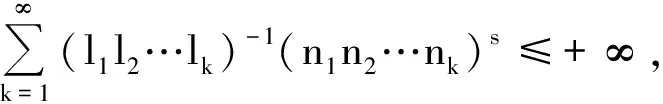
引理3[3]若集合E是一个齐次Moran集，则dimHE=sup{s|Cs(E)>0}.

定义闭球序列Bk(x)={y||y-x|≤c1c2…ck}，k=1,2，…，B0=R3-B1,则

其中,ψk(t)=min{t-s,(c1c2…ck)-s}，Em=E∩Bm，Ei=E∩(Bi-Bi+1)，i=0,1,2,…,m-1.

选取常数A和B，使得J包含半径为A的球，被包含在半径为B的球中，则对∀σ∈Dk，Jσ包含一个半径为Ac1c2…ck的球，并含于半径为Bc1c2…ck的球中，由于k阶基本元内部两两互不相交，Bk与ω(A,B)个Jσ(σ∈Dk)相交，从而φ-1(Bk)也与ω(A,B)个Cσ(σ∈Dk)相交，这里ω(A,B)为常数，且ω(A,B)≤[(2+B)A-1]3，故

由引理2知Is(μ)有界，且Cs(E)>0；结合引理1，引理3可得dimHE≥β.

综上(1)，(2)可得定理的正确性.