尾座式无人机续航时间估算模型

刘文帅 姚小敏 师志强 淡煦珈 韩文霆

(1.西北农林科技大学机械与电子工程学院， 陕西杨凌 712100； 2.农业农村部农业物联网重点实验室， 陕西杨凌 712100；3.固安县人民政府办公室， 固安 065500； 4.南京禾谱航空科技有限公司， 南京 211300；5.西北农林科技大学水土保持研究所， 陕西杨凌 712100)

0 引言

农田作物信息的快速获取与解析是开展精准农业实践的前提和基础，是突破制约中国精准农业应用发展瓶颈的关键[1-6]。农业遥感无人机主要通过搭载不同的遥感传感器如可见光相机、多光谱相机、热红外相机、高光谱相机和雷达等，进行农作物信息的采集[7-11]。无人机遥感以其在云下低空飞行的优势，弥补了卫星光学遥感和普通航空摄影易受云层遮挡的缺陷，成为农业遥感中不可或缺的手段[12-15]。现有的农业无人机主要是固定翼和多旋翼，多旋翼无人机凭借其起降方便和定点悬停的特点在农业遥感领域得到广泛应用，但由于其续航时间短、效率低而无法进行大面积信息采集；固定翼无人机具有工作效率高、续航时间长的特点，可进行大面积遥感信息的采集，但其无法进行精准起降，对起降场地有较高要求。垂直起降无人机的出现弥补了多旋翼无人机续航时间短和飞行效率低的缺点，解决了固定翼无人机精准起降控制难的问题，可以满足日益复杂的农业低空遥感任务需求[16-19]。现有的垂直起降无人机主要有尾座式、复合直升机式、倾转旋翼式、倾转机翼式、倾转涵道式和旋翼/机身转换式等[20]，其中尾座式无人机以结构简单、质量轻和操控方便的特点在近几年得到广泛关注[21]。现有尾座式无人机的研究主要集中在不同飞行状态下的控制算法优化、基于飞行气动特性的结构参数优化和基于飞行参数的飞行效率优化3方面[22-27]。国内外一些学者对尾座式无人机的姿态控制算法、PID调参、起降分析、升阻比特性和续航时间估算等进行了研究。如SILVA等[28]为研究垂直起降无人机在整个作业过程中的飞行姿态控制，采用动态拟合增益调度的控制方法建立无人机的运动方程，并与实际飞行的PID控制器进行对比分析，控制误差在20%以内。许景辉等[29]采用四元数互补滤波的方法对倾转三旋翼垂直起降无人机悬停姿态控制进行了优化。LIANG等[30]利用目标角度算法和PID姿态控制算法，实现了尾座式无人机垂直方向和过渡过程中俯仰角和姿态的控制。BEACH等[31-32]利用误差四元数控制算法和矢量分量驱动器进行了尾座式无人机全方面姿态的模拟控制分析。KNOEBEL等[33]结合动力学模型的反推算法和加权递推最小二乘法，进行自适应四元数控制算法的研究，解决了尾座式无人机转换过程中的姿态控制问题。NOGAR等[34]为提高尾座式无人机飞行效率，降低姿态转化能耗，为现有无人机设计了倾转机构，并进行了控制算法优化，增加了无人机的续航时间。为增加现有飞翼无人机的续航时间，师志强[35]采用CFD仿真的方法对无人机的翼展长和后掠角进行了优化，优化后的无人机续航时间增加了36%。刘玉焘[36]从无人机结构设计、气动分析以及在不同角度下机身的气动分布，阐述了尾座式无人机的设计过程，但没有进行续航时间的研究。为提高电动无人机续航时间，刘伏虎等[37]以起飞质量和巡航升阻比为优化目标，采用遗传算法对无人机的总体结构参数进行了优化，并在Matlab中进行模拟仿真，但并未阐述结构参数与续航时间的关系。AKSUGUR等[38]提出了新型的混合动力无人机概念设计，并进行了混合动力推进系统的设计和优化。WANG等[39-40]利用飞行空间、翼载荷和电池的组合分析，进行尾座式无人机的飞行参数优化，并利用电池放电曲线和飞行参数进行了空间距离估算。刘胜南[41]针对多旋翼无人机续航时间实时估算问题，提出了无人机不同飞行状态下的能量消耗估算方法。

续航时间是尾座式无人机的性能参数，也是无人机结构优化的一个重要指标，现有学者在结构优化、飞行参数优化和能耗估算等方面进行了无人机续航的研究，但未阐述清楚尾座式无人机结构参数与续航时间的关系。本文围绕续航时间，进行不同结构参数的单因子多水平试验设计，并对无人机续航时间进行数值模拟，建立续航时间与结构参数的关系模型，为长续航尾座式无人机的结构优化提供理论依据。

1 材料与方法

1.1 尾座式无人机结构及参数范围

1.1.1结构布局

尾座式无人机采用飞翼式对称布局设计，主要由机翼、舵面、小翼、电机座、电机和螺旋桨组成，如图1所示，小翼、舵面和电机座固定在机翼上，电机和螺旋桨在机身纵向轴线上，根据起飞质量的不同选择双动力前拉式或单动力尾推式。

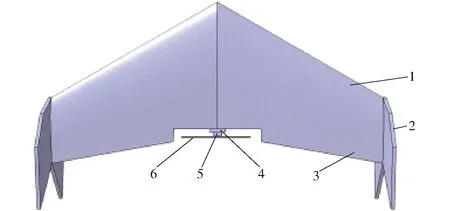
图1 尾座式无人机示意图Fig.1 Schematic of tail-sitter UAV1.机翼 2.小翼 3.舵面 4.电机座 5.电机 6.螺旋桨

尾座式无人机通过电机转速和舵面调节，实现垂直起降、过渡和巡航3种飞行模式的姿态控制。无人机垂直起飞时，以多旋翼的模式进行垂直起飞，达到一定高度后，电机转速增加，舵面为飞机提供一个低头力矩，使无人机进入平飞状态，转换为固定翼飞行模式，飞向作业区域进行遥感信息采集；降落时，电机转速降低，降低固定翼模式的飞行速度，当降到一定速度时，舵面提供一个抬头力矩，将机头拉起进入多旋翼垂直降落模式。

从整体的作业飞行过程可知，无人机固定翼模式下的匀速巡航状态占总续航时间的95%，因此本文研究尾座式无人机巡航状态下结构参数与续航时间的关系。

1.1.2结构参数范围

本文研究的尾座式无人机为左右对称结构，选择无人机中轴线左侧进行分析。影响无人机续航时间的主要结构参数(图2)为翼展长b、翼根弦长cr、翼梢弦长ct、机翼后掠角Λw、小翼翼梢长lys、小翼展长bv、小翼高lv、小翼后掠角Λv、小翼厚度h和小翼脚长ljc(小翼两个支撑脚的距离)。

图2 影响续航时间的结构参数Fig.2 Structural parameters affecting endurance time1.机翼 2.小翼

本文从现有无人机的结构参数范围、文献中的结构参数范围以及垂直起降稳定性3方面进行结构参数范围的确定。

农业上常用的电动固定翼遥感无人机主要为瑞士的sensefly、senseflyeBee，法国的Parrot Disco-Pro和国内的天行者X5，由制造商的官网数据得到电动固定翼无人机的参数如表1所示。

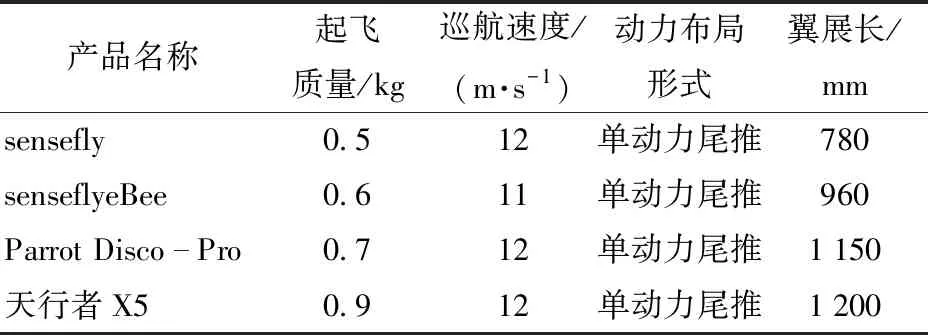
表1 常用电动固定翼无人机参数Tab.1 Electric fixed wing UAV parameters

由表1可知，现有无人机的翼展长范围为780～1 200 mm，因此选定b的范围为800～1 200 mm；考虑飞控、数传等设备的内嵌安装，选定cr的范围为240～500 mm。

由文献[42-43]中常用小型飞翼无人机的根梢比(0.2～0.4)、后掠角(0°～60°)、小翼后掠角(25°～60°)和小翼高(0.05b～0.3b)的范围，确定ct的范围为150～300 mm，Λw的范围为0°～60°，Λv的范围为30°～60°，lv的范围为30～60 mm。

现有的农用无人机多采用EPP材料，考虑机翼刚度选择h的范围为5～25 mm；考虑无人机垂直起降时机身的纵向稳定性选择bv的范围为150～200 mm，lys的范围为100～130 mm，ljc的范围为70～150 mm。

无人机的续航时间与起飞质量、飞行速度、动力系统布局和结构参数等因素有关。动力系统的布局形式是飞行效率的直接影响因素，起飞质量是动力系统布局的重要选择依据，也是巡航速度的重要影响因素。本文主要研究结构参数与续航时间的关系，从单一变量试验原则出发，根据表1中无人机的参数，确定本文的飞行速度为12 m/s，起飞质量为0.6 kg，动力系统布局形式为单动力尾推式。

1.2 无人机外流场数值模拟方法

为获取无人机在不同参数下的续航时间，需要对无人机的外流场进行数值模拟。由于无人机采用左右对称布局，因此采用中轴线左侧作为研究对象进行数值模拟分析。利用CATIA建立尾座式无人机的三维实体模型，建模过程中对模型进行简化，去掉了螺旋桨、电机座和电机等结构。将建立好的无人机三维模型导入到ANSYS Workbench的Geometry模块，并创建一个5 m×5 m×3 m的外流场区域，采用布尔运算得到无人机外流场的三维实体模型，并对入口、出口、流场壁面、流场对称面和无人机壁面进行设置。利用ANSYS的ICEM模块对外流场进行结构体网格划分，如图3所示，网格数量为300万，节点数量为224万，将网格导入CFX进行外流场数据模拟计算。

图3 无人机外流场网格Fig.3 Grids of UAV outflow

假设气体在低速流动下为粘性不可压缩流体，当雷诺数超过2 300时产生湍流，选用SSTk-ω模型对无人机外流场进行CFD数据模拟。入口速度为12 m/s，出口压力为标准大气压，计算区域的边界假定为无滑移条件。用标准的边界方程对无人机进行近壁面处理，用SIMPLE算法求解方程。用该方法对10个结构参数进行仿真分析得到130组外流场数值模拟结果。

1.3 结构参数与续航时间关系模型建立方法

1.3.1续航时间理论模型

无人机续航时间主要与电池电量、起飞质量和气动特性三者相关，由文献[44]可知无人机的续航时间可以表示为

(1)

(2)

(3)

(4)

则续航时间可以表示为

t=QtFA=QGFACFA

(5)

式中t——续航时间,s

Q——电池放电能量,J

GFA——质量系数,s/J

CFA——气动系数

tFA——时间系数,s/J

ρ——空气密度,取1.185 kg/m3

s——无人机投影面积,m2

G——无人机重力,N

CD——阻力系数

CL——升力系数

由式(1)～(5)可知，在电池能量一定的情况下，无人机的续航时间主要由质量系数GFA和气动系数CFA决定，因此若要建立结构参数与续航时间的关系模型，需要分别建立结构参数与GFA和CFA的关系模型，并通过两者的联立最终建立结构参数与续航时间的关系模型。

无人机续航时间与重力、飞行效率、结构参数等因素有关，其中重力与无人机的材料、结构、动力系统、飞行速度密切相关，当无人机重力增大时，飞行效率下降，续航时间缩短；当无人机重力减轻时，飞行效率增加，续航时间增大，即重力直接影响无人机的续航时间。本文从单一变量的原则出发，研究重力为定值情况下，结构参数与续航时间的关系。

1.3.2结构参数特征因子提取方法

在质量系数和气动系数关系模型的建立过程中，为提高模型精度，降低冗余度，需要对结构参数进行特征因子筛选，本文采用几何分析的方法进行质量系数特征因子的筛选，采用回归方程构建和方差分析的办法进行气动系数特征因子的筛选。

(1)质量系数

由式(2)可知，质量系数主要由重力和投影面积决定，本文中无人机的重力为定值，因此质量系数只与无人机投影面积相关。构建无人机投影面积的几何模型，通过分析各结构参数在几何模型的影响权重，确定质量系数的特征因子，本文中机翼面积远大于小翼面积，因此质量系数的特征因子为翼根弦长、翼梢弦长和翼展长。

(2)气动系数

为分析气动系数的特征因子，在R软件中分别建立10个结构参数与气动系数的一元回归方程，并对回归方程进行方差检验，通过对比10个回归方程的显著性P值、决定系数R2和均方根误差(RMSE)进行特征因子筛选，结果如表2所示。

表2 气动系数特征因子提取指标Tab.2 Extraction index of aerodynamic coefficient characteristic factor

由气动系数特征因子提取指标可知，当P≤0.05时，可确定该因子为特征因子；当P>0.05表明该因子不是特征因子。对于特征因子与气动系数的关系，需要结合R2和RMSE进行关系模型的二次筛选。当R2≥0.5且RMSE小于等于0.15，表明该因子与气动系数为一次线性关系；当R2≥0.5且RMSE大于0.15时，表明该因子与气动系数为非线性关系；当R2<0.5表明该因子与气动系数之间为非线性关系。

为提高气动系数模型精度，需要确定特征因子的非线性关系，本文采用曲线拟合的方法。利用Excel对特征因子和气动系数分别进行曲线拟合，对比拟合曲线的决定系数进行特征因子非线性关系的确定。最终确定的气动系数的特征因子为翼展长、后掠角、小翼厚度和小翼脚长。

1.3.3续航时间关系模型建立方法

利用R软件构建翼根弦长、翼梢弦长和翼展长3个特征因子与质量系数的三元回归模型；建立翼展长、后掠角、小翼厚度和小翼脚长4个特征因子与气动系数的的四元回归模型；结合续航时间理论模型最终建立结构参数与续航时间的多元回归模型。

1.4 试验方案设计与试验验证

采用单因素多水平试验设计的方法建立结构参数与续航时间关系模型，并采用样机试飞的方法进行关系模型的试验验证。

1.4.1结构参数试验设计

为研究结构参数与续航时间的关系，需要对无人机的10个结构参数进行组合分析，考虑各结构参数的影响权重，为各结构参数设计了不同的水平，从中抽取130组不同结构参数的组合进行续航时间的数值模拟计算，如表3所示。

表3 无人机结构参数试验设计Tab.3 Experiment parameters of UAV

对10个结构参数进行了130组模拟计算，以翼展长为例进行不同结构参数的三维模型图展示。翼展长的范围为800～1 200 mm，共20个水平，选取800、860、900、1 000 mm共4个尺寸绘制的三维模型如图4所示。

图4 不同翼展长时无人机三维模型Fig.4 3D models of UAV with different wingspan sizes

1.4.2验证方法

1.4.2.1数值模拟结果验证方法

(1)风洞试验材料与设备

续航时间的回归模型主要由质量系数和气动系数两部分模拟数据组成，本文中质量系数只与投影面积相关，可由几何尺寸进行准确计算；气动系数主要与样机的升力系数和阻力系数相关，采用风洞试验的方法进行数值模拟结果准确性的验证。在130组模拟结果中选择4组制作样机(表4)，并在8°攻角、风速为20 m/s的巡航状况下进行风洞试验，根据风洞试验的相似准则将无人机模型的翼展长等比缩放到600 mm，并采用三维打印技术进行模型的加工，如图5所示。

表4 风洞试验样机参数Tab.4 Parameters of wind tunnel test sample

图5 风洞试验样机Fig.5 Wind tunnel test sample

风洞试验系统包括无人机模型、飞机支架、六分量应变天平、风机、变频器和数据采集控制系统等，如图6所示。试验中通过飞机支架将无人机攻角稳定在8°，并通过变频器将风速稳定在20 m/s，通过六分量应变天平进行无人机升力系数和阻力系数的采集，并由数据采集控制系统进行数据的记录分析。

图6 风洞试验系统示意图Fig.6 Wind tunnel test system1.六分量应变天平 2.无人机模型 3.飞机支架 4.风机 5.变频器 6.数据采集系统

(2)风洞试验条件与方案

风洞试验在西北工业大学翼型叶栅空气动力学国家重点实验室内进行，该风洞场地长5 m、宽4 m，提供风速0～20 m/s的变频器及试验测量系统，实验室内气温为5～8℃，如图7所示。进行4架无人机样机的风洞试验。

图7 样机风洞试验Fig.7 Prototype wind tunnel tests

1.4.2.2续航时间模型验证方法

为验证续航时间模型，根据仿真结果选择翼展长分别为800 mm和860 mm的两架样机进行加工，如图8所示。

图8 无人机样机Fig.8 Tail-sitter UAV samples

无人机样机的参数主要包括翼根弦长、翼梢弦长、翼展长、后掠角、小翼厚度和小翼脚长，如表5所示。

无人机试验系统包括Pixhack飞行控制系统、电量测试系统、朗宇X2206 KV1500电机、天行者15 A电子调速器、APC8040螺旋桨、3S 1 500 mA·h 25c电池、PIX数字空速计和3DR数传通信系统等。

无人机采用手抛起飞，待飞行平稳后切换成自驾模式进入预定飞行航线(高度100 m、半径100 m)定点盘旋，通过Mission Planner地面站进行实时飞行监测和电池电量记录，如图9所示。

表5 试验样机参数Tab.5 UAV samples parameters

图9 无人机地面站实时监测系统Fig.9 UAV ground station monitoring system

图10 无人机试飞试验Fig.10 UAV flying test

无人机试飞试验在中国旱区节水农业研究院室外试验田进行，场地空旷且没有障碍物干扰，试飞当天天气晴朗，平均气温22℃，地面风速1级(0.3 m/s)，满足试飞条件，进行飞前准备如图10所示。两架样机连续记录剩余电量为90%、80%、70%、60%和50%时无人机的飞行时间，重复测定3次取平均值，共计6次试验。

2 结果与分析

2.1 尾座式无人机外流场气动特性

在130组数值模拟结果中气动系数的变化范围为5～7.8，其中翼展长、后掠角、小翼厚度和小翼脚长4个结构参数变化时，气动系数的变化范围为5.2～7.8，变化幅度达93%，剩余6个结构参数的变化对气动系数的影响幅度为7%，由此可知，翼展长、后掠角、小翼厚度和小翼脚长4个结构参数是气动系数主要影响因素，4个结构参数与气动系数的散点图如图11所示。

由图11可知，当翼展长从800 mm增加到1 200 mm过程中，气动系数从5.2增加到7.2，并且翼展长与气动系数为一次线性关系。小翼厚度从5 mm增加到25 mm的变化过程中，气动系数从7.8逐渐减小到7.1；小翼脚长从70 mm增加到150 mm的过程中，气动系数从7.7逐渐减小到7.2，两个结构参数与气动系数呈一次线性负相关。当后掠角从0°增加到30°的过程中，气动系数7.2保持不变，当后掠角超过30°，气动系数迅速减小到5.5；后掠角与气动系数之间呈二次多项式关系，其拟合方程在2.2.2节中分析。

图11 结构参数与气动系数散点图Fig.11 Scatter diagrams of structural parameters and CFA

对于飞翼垂直起降无人机，无人机的气动特性主要由翼型沿翼展方向的气动系数积分所决定。以50 mm为积分单元，分别绘制不同翼展长和不同后掠角时沿展向的气动系数分布，如图12所示。

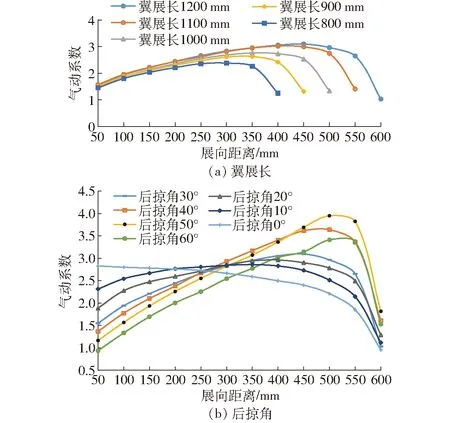
图12 翼展长与后掠角的展向气动系数分布Fig.12 CFA spanning distributions

由图12a可知，不同翼展长在同一积分单元内的气动系数相近，积分单元在翼梢位置处的气动系数迅速减小。积分单元沿展向距离的积分为机翼的气动系数，并且积分只与翼展长有关，因此翼展长与无人机的气动系数呈线性正相关。

由图12b可知，不同后掠角在同一位置处的气动系数不同，因为后掠角的改变，影响了翼型的来流分布，进而影响了气动系数。当后掠角在0°～30°变化时，不同后掠角沿展向距离的积分相同，即随着后掠角的增加，气动系数保持不变；当后掠角在30°～60°变化时，不同后掠角沿展向距离的积分逐渐减小，即随着后掠角的增加，气动系数逐渐减小。

无人机的气动系数主要由翼型沿翼展方向的气动系数积分所决定，如图13a所示，其中Δd为翼型在翼展方向的积分单元。由图可知，当翼展长由b增加到b1时，Δd上的气动系数相同，因此机翼的气动系数只与翼展的长度相关，即翼展长与气动系数呈线性关系。当机翼的后掠角增加时，Δd的来流方向没有发生变化，Δd上的气动系数发生改变，因此机翼的气动系数与后掠角呈非线性关系。

图13 气动系数分布机理Fig.13 CFA distribution mechanism

由图13b可知，沿翼展方向机翼的速度流线分布均匀，因此不同翼展长在同一位置处的气动系数相同。在翼梢附近由于翼尖扰流的作用，小翼附近的流场分布发生突变，并出现载荷泄载。

2.2 续航时间关系模型建立

2.2.1质量系数特征因子

在起飞质量一定时，无人机的质量系数只与投影面积相关。尾座式无人机的投影面积几何图形如图2b所示。无人机的投影面积主要由小翼和机翼两部分组成。其中小翼的投影面积主要由小翼厚度h、小翼翼梢长lys和小翼展长bv3个结构参数决定；机翼主要由翼根弦长cr、翼梢弦长ct和翼展长b3个结构参数决定。当h=25 mm、lys=130 mm和bv=200 mm时，取得小翼的最大面积为0.008 m2；当cr=500 mm、ct=150 mm、b=800 mm时取得机翼的最小面积为0.26 m2，对比可知机翼面积是小翼面积的32倍。因此无人机的投影面积主要由机翼的投影面积决定，即质量系数的特征因子为翼根弦长、翼梢弦长和翼展长。

2.2.2气动系数特征因子

利用130组仿真数据对结构参数进行特征因子筛选，分别构建10个结构参数与气动系数的一元回归方程，共得到10个一元回归方程，对回归方程进行回归检验和方差分析，结果如表6所示。

由P>0.05可知，翼根弦长、翼梢弦长、小翼翼梢长、小翼展长、小翼高和小翼后掠角6个结构参数不是特征因子。由P≤0.05可知翼展长、后掠角、小翼厚度和小翼脚长是气动系数的特征因子。由R2≥0.5和RMSE大于等于0.15的二次筛选结果可知，翼展长、小翼厚度和小翼脚长3个特征因子与气动系数呈一次线性关系，后掠角与气动系数呈非线性关系。

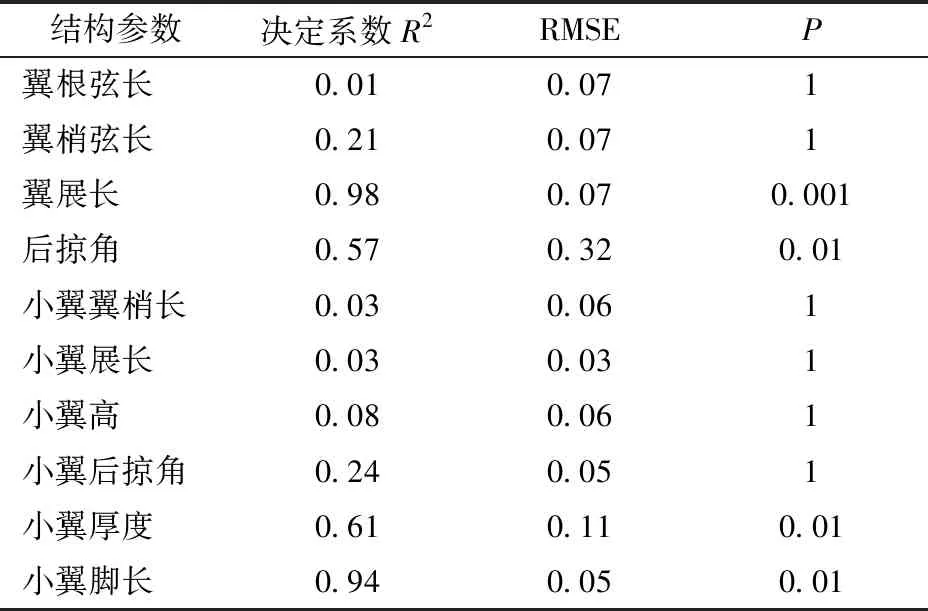
表6 结构参数回归分析Tab.6 Regression analysis of structural parameters

采用曲线拟合的方法，确定后掠角的非线性拟合项。在130组模拟值中提取后掠角对应的12组气动系数模拟值，在Excel中分别进行指数、对数和二次多项式3种函数的曲线拟合，结果如图14所示。

图14 后掠角曲线拟合Fig.14 Fitting curves of sweep angle

2.2.3气动系数关系模型

(6)

将方程预测结果与CFD模拟结果进行对比，结果如图15所示。

图15 气动系数多元回归模型Fig.15 Multivariate regression model of aerodynamic coefficients

方程预测结果与仿真结果分布于一条直线上，且方程预测精度为0.977，均方根误差为0.105，方程可靠。因此翼展长、后掠角、小翼厚度和小翼脚长的四元回归方程可以进行气动系数的估算。

2.2.4续航时间关系模型

在130组CFD仿真数据中，提取翼根弦长、翼梢弦长和翼展长3个特征因子所对应的49组仿真数据。利用R软件构建翼根弦长、翼梢弦长和翼展长3个自变量与质量系数的三元一次回归方程为

(7)

质量系数的回归方程精度为0.99，因此翼根弦长、翼梢弦长和翼展长的三元一次回归方程可以进行质量系数的估算。

联立式(5)～(7)，可知无人机续航时间的方程为

(8)

由式(8)可知，无人机的续航时间可以通过电池电量、起飞质量、无人机的翼根弦长、翼梢弦长、翼展长、后掠角、小翼厚度和小翼脚长的几何参数计算得到。起飞质量与电池电量直接相关，因此当无人机质量为定值时，可以通过续航时间模型进行无人机结构参数的优化，模型精度为0.97。

2.3 试验结果验证

2.3.1风洞试验结果

将表4中的4个样机的仿真结果与风洞试验结果进行对比，结果如表7所示。

由表7可知，试验气动系数与仿真气动系数的相对误差为9.9%～13.7%。误差原因分析：采用三维打印进行模型的加工，模型的表面颗粒和粗糙度会影响机身近壁面的流场分布；模型阻力较小，在风洞试验过程中的信号干扰等因素均会影响阻力系数的测量精度；仿真过程中采用无人机模型的一半进行建模和仿真计算，影响无人机在对称面处(翼根)流场的仿真精度。但试验结果相对误差在14%以内，在允许的误差范围内，表明数值模拟方法可靠，能够进行无人机气动系数的准确估算。

表7 风洞试验结果与仿真结果对比Tab.7 Comparison between wind tunnel test and simulation results

2.3.2无人机试飞试验结果

将表5中两架样机的结构参数代入式(8)，计算得到样机的方程预测续航时间，将方程预测续航时间与试验续航时间对比，结果如表8所示。

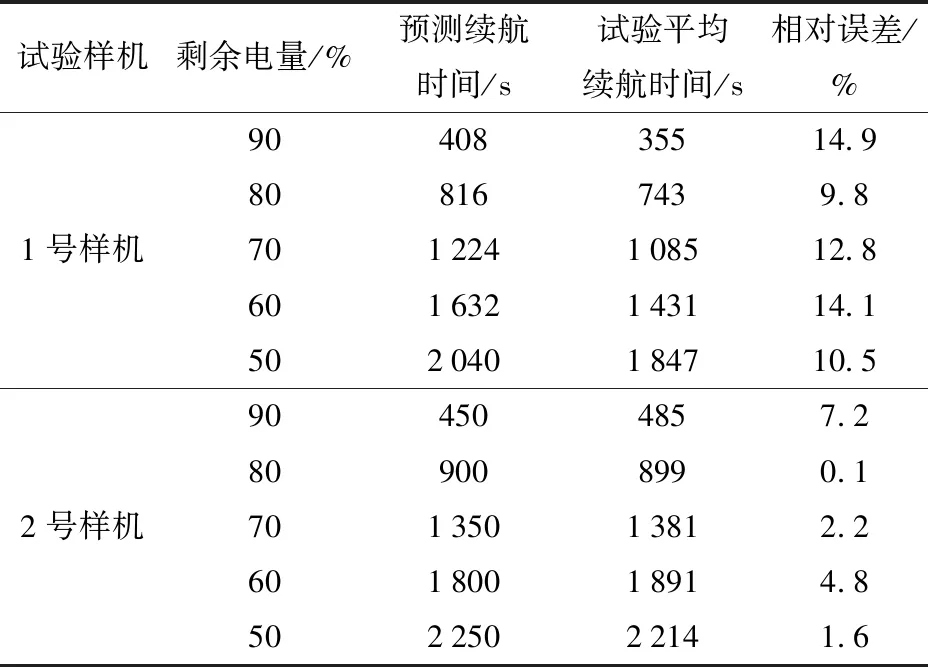
表8 试验结果与预测结果对比Tab.8 Comparison between test and simulation results

1号样机和2号样机试验续航时间与预测续航时间相对误差在15%以内，在误差允许范围内，表明仿真数据可靠，因此由130组模拟数据建立的结构参数与续航时间的关系模型可靠。1号样机与2号样机由于翼展长和后掠角两个结构参数的不同，导致续航时间存在差异，本文建立的关系模型可预测续航时间的变化规律，因此该模型可用于尾座式无人机结构参数优化。

通过对误差的分析发现，误差产生的主要原因是试验环境、样机制作工艺和实际飞行效率等因素，因此本文建立的结构参数与续航时间的关系模型具有较高精度，可以为长续航尾座式无人机的设计提供依据。

3 结论

(1)建立了无人机及其外流场的三维实体模型，对130组不同参数组合下的气动特性进行数值模拟，利用方差分析确定了气动系数的特征因子为翼展长、后掠角、小翼厚度和小翼脚长，其中气动系数与翼展长呈线性正相关、与后掠角呈二次负相关，与小翼厚度和小翼脚长呈线性负相关。利用几何分析确定了质量系数的特征因子为翼根弦长、翼梢弦长和翼展长，质量系数与三者呈线性正相关。

(2)融合翼展长、后掠角、小翼厚度和小翼脚长4个特征因子建立了气动系数的四元二次回归模型，结合质量系数的三元回归模型，最终建立了续航时间的关系模型，模型精度达0.97。

(3)采用等效缩放的方法对4架样机进行无人机风洞试验，记录无人机在巡航状态下的气动系数，并对数值模拟结果进行误差分析，结果表明风洞试验数据与仿真计算数据的误差在14%以内，模拟方法可靠。

(4)采用手抛起飞，定点定高盘旋的方法对无人机样机进行试飞试验，实时记录无人机在不同剩余电量时的续航时间，并对模拟结果进行误差分析，结果表明试验数据与预测数据的相对误差在15%以内，模型可靠。