关于L-函数一类特殊二次均值的计算问题

段 然

(西北大学 数学学院, 陕西 西安 710127)

设整数q满足2≤q∈N+, 且χ是模q的一个Dirichlet特征, 记为χmodq。当一复数s对应的实部Re(s) 满足Re(s)=σ>1 时, 定义函数L(s,χ) 为

这就是在解析数论研究过程中起到重要作用的DirichletL-函数。

若χ是模q的主特征即χ=χ0, 则L(s,χ) 除在s=1处外是处处解析的,s=1 是DirichletL-函数的一个一阶极点, 并且其留数为φ(q)/q, 其中φ(q)为Euler函数。

若χ不是模q的主特征, 即χ≠χ0, 那么函数L(s,χ)是关于其变元s的整函数。Dirichlet对算术级数中的素数分布问题做了大量的工作, 同时引入了函数L(s,χ)。关于DirichletL-函数性质的研究概括起来有以下三大方面:

1)L-函数的零点密度问题;

2) 带有权系数的L-函数的均值问题的研究;

以上任何一个方面所取得的进展,必将对解析数论,甚至于对整个数论科学的发展起到巨大的推动作用。

1 概况L-函数均值研究

1.1 L-函数高次均值的研究进展

本文研究了DirichletL-函数在直线s=1上一类特殊二次均值的计算问题。事实上, DirichletL-函数在直线s=1上的二次均值计算问题是解析数论, 甚至整个数论科学中的一大热点问题。 有关这一问题, H. Walum[1]进行了研究, 并证明了如果整数q为奇素数p时, 存在等式

(1)

并且H. Walum[1]研究L-函数时发现了Dedekind和与L-函数加权均值间的关系式, 即得到了等式

张文鹏将等式 (1) 推广到对一般整数模q的情况。即文献[2] 的作者张文鹏证明了对任意整数q≥3, 存在下述等式:

随后, 张文鹏[3]获得了一个更加深入的结果。即当q是一个奇的Square-full数时, 其证明了下述等式:

上述结果都是DirichletL-函数在直线s=1上的二次均值计算问题的具有代表性的重要结论。 除以上所述外, 当然还有很多关于DirichletL-函数在直线s=1上的二次均值计算问题的研究内容。 这些内容可参看文献[4-8] , 这里不再一一赘述。

总结以上这些均值公式, 可以发现它们的共同之处体现在均是对模q的奇特征求和。 对偶特征情形下的类似问题, 几乎没有一篇论文涉及。造成这一现象的原因是此类均值在偶特征情形下可能不存在确且的计算公式。

1.2 L-函数特殊二次均值的研究进展及本文结果

最近, 对于模q的偶特征χmodq,χ(-1)=1, 朱敏慧和杨晓柳[9]研究了另一类二次均值的计算问题, 即和式

(2)

的计算问题, 其中q≥3 为整数,λ为模r的奇特征, 这里r≥3 且(q,r)=1。

并且文献[9] 的两位作者得到了下述结论:

1) 若3≤q∈N+，且q是奇数,χ4为模4的特征且χ4≠χ0, 则存在等式

其中φ是Euler函数。

2)若q∈N+,(q,3)=1,χ3为模3的特征且χ3≠χ0, 则有恒等式。

因φ(3)=φ(4)=2, 从而模 3 和模 4 各自都只有一个奇特征χ3,χ4。 同时注意到对分解式k=k1·…·kl而言(其中k1,…,kl两两互素)，模k的任一特征χ(n;k) 可分解为唯一的一组模k1的特征χ(n;k1)。模kl的特征χ(n;kl) 的乘积, 即χ(n;k)=χ(n;k1)，…，χ(n;kl)。 据此分析, 文献[9] 中结果的实质是对模 3q及 4q的全体奇特征求和的问题。

另一方面, 由于模 3=31和模 4=22各自都只是一个素数的方幂, 因此相关的证明过程及计算过程处理起来比较简单容易。 但是，如果求和式 (2) 中的r是两个或两个以上不同素因数的乘积, 甚至说是两个或两个以上不同素因数方幂的乘积时, 相关的证明过程及计算过程处理起来就复杂了, 有时所面临的困难甚至是无法逾越的。 我们仅仅以r=6 为例, 研究求和式 (2) 的计算问题, 并给出一个确切具体的计算公式。 同时指出文献[9] 中定理 2 的不足之处。

换言之我们将证明下面的两个结论。

定理1设q∈Z,q≥3,(q,6)=1, 且χ6为模6 的奇特征, 如果 ∅≠{d∈N+:d|q}⊆{6n+1:n∈Z}, 那么得到

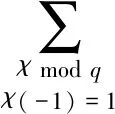
定理2设p为奇素数且p≡-1 mod 6, 那么对模6 的唯一一个奇特征χ6, 存在等式

注释:

1)本文定理1的预设条件中, 要求对q的每一个正因数d需满足同余条件d≡1 mod 6是必要的。 因为当q≡1 mod 6时, 并不能保证整数q的每一个因数d满足该同余式, 如整数25。从而如果不要求对q的每一个因数d都必须满足同余关系d≡1mod 6时, 就会导致我们在定理的证明过程中无法使用Möbius反转公式

2 必要的引理

为了证明本文定理,需要借助一些引理及著名和式Dedekind和, 并大量运用Dedekind和的性质。 当然还需借助初等数论的知识, 关于Dedekind和的性质及用到的初等数论内容可参阅文献[10-12] 。

首先需要指出的是Dedekind和是在研究η函数在模变换下的性质时引进的。经典Dedekind和的定义如下:

设q∈N+,h∈Z, 经典Dedekind和S(h,q)定义为

其中

此处借助高斯函数[x] 的性质易见函数((x)) 以任意非零整数作为其周期。

经典Dedekind和的算术性质的研究吸引了不少学者。 关于经典Dedekind和的一系列重要结果和性质可参阅文献[11] 及[13-17] 。这里需要强调的是L.Carlitz在文献[13] 中给出了Dedekind和S(h,q) 的互反公式, 即当q∈N+,h∈N+,(h,q)=1 时, 存在恒等式

(3)

其次,我们引入完成本文定理证明所需要的一些引理。

引理1如果 3≤q∈N+,h∈Z(h,q)=1, 则存在等式

证明其证明可参阅文献[4] 中引理 2。

文献[4] 的作者张文鹏发现了上述引理, 其深远的意义在于建立了Dedekind和与DirichletL-函数二次加权均值之间的直接联系。

引理2(i) 若3≤q∈N+,且q是奇数, 则存在等式

(ii)若 (q,3)=1, 则存在公式

证明其证明可参考文献[9] 中的引理2。

引理3设3≤q∈Z,(q,6)=1, 那么

证明依据Dedekind和的定义知

(4)

借助等式(4)及Dedekind和的互反公式(3)立刻推出，当q≡1 mod 6 时, 有

(5)

当q≡-1 mod 6时,结合S(-1,6)=-S(1,6)得出

(6)

综合等式 (5) 及 (6) 即完成了引理 3 的证明。

引理4若 3≤q∈Z,(q,6)=1, 则

当q≡1 mod 6时,依据Dedekind和的互反公式(3)得到

(7)

当q≡5≡-1 mod 6时,由式(7)的证明方法，有

(8)

由等式(7)及等式(8)立刻推出引理4。

3 定理的证明

本节我们来完成定理的证明。

定理1的证明借助初等数论的知识可得[18]

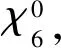
对模q的奇特征χmodq, (其中 3≤q∈Z) 存在等式

(9)

(10)

|L(1,χ)|2=Δ·|L(1,χ)|2,

(11)

其中

(12)

利用引理1, 引理2及等式(9)立即推出

(13)

(14)

当q≡1 mod 3时,由文献[9] (参阅该文中的 (16) 式) 知

(15)

由式(11)及引理 3 得到

(16)

所以将等式 (13)～(16) 代入等式 (12)，并化简计算得

(17)

另一方面, 由Dedekind和的定义可以得到

(18)

利用等式(17)及等式(18)建立方程得到如下求和式:

对上式施用Möbius反转公式立即得到

其中μ是Möbius函数。

于是定理1得证。

注释:结合上述本文定理 1 的证明推导过程, 可见文献[7] 中的结果在最后一步用到Möbius反转公式时是不正确的!因为当q≡1 mod 6 时,q的每一个正因数d不一定满足同余式d≡1 mod 6。所以不能直接使用该文中的引理2,必须加上本文中的限制条件才可以使用!

定理2的证明完全类似地按照引理2、引理3、引理4以及等式(12)、等式(17)和等式(18)的证明方法可得

(19)

(20)

当q≡-1 mod 3时,由文献[9] (参阅该文中的(15)式) 知

(21)

由式(21)容易推出

(22)

结合等式 (12), 等式 (18)～(20)及等式(22)可立刻推出

将上式简化后得

于是定理2得证。