一种带变异算子的自适应惯性权重二进制粒子群优化算法

王 越,邱飞岳，郭海东

(浙江工业大学 教育科学与技术学院,杭州 310023)

1 引 言

粒子群算法(Particle Optical Swarm)是由美国心理学家James Kennedy和电气工程师Russell Eberhart[1]在1995年提出的一种自适应群体智能搜索算法,由于PSO算法所需调节的参数较少,概念简单且容易实现,已被广泛应用于神经医学、网络训练和运筹学等领域的优化问题[2-4].由于在实际应用当中很多问题是离散型的问题,因此,James Kennedy和Russell Eberhart在1997年又提出一种二进制粒子群算法(Binary Particle Optical Swarm)[5],用来解决离散性的优化组合问题.二进制粒子群优化算法也已被很多领域广泛应用,例如背包问题[6]、电力系统[7]、数据挖掘[8,9]、图像处理[10]等.BPSO算法寻找最优解依靠粒子间信息传递与共享的特征决定了算法种群多样性和搜索性能对算法的收敛速度和收敛精度起主要作用.但二进制粒子群算法不能动态调整粒子群算法的搜索范围,因为它的惯性权重值不能随种群迭代动态改变,这就引起了二进制粒子群算法会随着种群多样性的下降,容易早熟收敛而陷入局部最优.针对这种二进制粒子群算法的缺点,很多学者都提出了各种改进方法.首先Chuang L Y等学者[11]采用混沌映射确定惯性权重值的方法提高二进制粒子群优化算法的性能.由于混沌映射的行为不存在固定点、周期轨道或准周期轨道.因此,改进的算法可以避免陷入局部最优.Mirjalili S等学者[12]采用惯性权重值线性减小的策略来优化二进制粒子群算法.然而,没有理论研究或分析能支持直接采用这种方法的有效性.Liu J等学者[13]证明了在二进制情况下,较小的惯性权重提高探索能力,而较大的惯性权重提高开发能力,所以提出了惯性权重线性增长的二进制粒子群优化算法.但在惯性权重值线性增长的过程中往往会忽略线性增长附近最优解的存在.

本文提出一种带变异算子的自适应惯性权重二进制粒子群优化算法(MABPSO).首先提出惯性权重的非线性递增策略,该策略确保惯性权重能够根据种群迭代进行自适应调整,使算法在迭代后期拥有较大的惯性权重,提高算法全局搜索能力,避免陷入局部最优;其次设计变异算子用于粒子的搜索过程,扩大粒子的搜索范围,进而提高二进制粒子群优化算法跳出局部最优的能力.通过测试函数表明该算法提高了收敛速度和收敛精度,同时避免了早熟收敛和陷入局部最优的问题.

2 二进制粒子群优化算法

在D维解空间中,有N个粒子组成一个群体x=[x1,x2,…,xN],每个维度下的粒子都可以由其速度向量信息和位置向量信息进行表示,粒子i的速度向量和位置向量表示如下:vi=[vi1,vi2,…,viD],xi=[xi1,xi2,…,xiD].第i个粒子的个体极值为pi=[pi1,pi2,…,piD];gi=[gi1,gi2,…,giD]表示种群的全局极值.当前粒子位置的优劣程度由适应度函数进行检测,达到最大迭代次数或最佳精度后,输出最优解.BPSO算法的速度和位置更新公式如式(1)、式(2)所示:

(1)

(2)

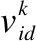
在BPSO中,用概率描述了粒子位置的变化和速度的变化状态.状态空间中粒子的位置用0或1表示,S(vid)代表xid取1的概率,基本公式如下所示:

(3)

(4)

其中,rand()是分布在[0,1]内的随机数,式(4)表示Sigmoid函数.

3 改进二进制粒子群优化算法

3.1 惯性权重非线性递增策略

在二进制粒子群优化算法中较小的惯性权重提高探索能力,而较大的惯性权重注重开发.通过文献[13]可知,对惯性权重进行线性优化虽然有助于提升算法性能,但是该策略不能有效满足算法的寻优过程,对开发和搜索性能不能达到有效平衡.因此,为了更加的接近算法寻优的实际进化状态,本文对惯性权重进行非线性递增优化.在每次迭代中,惯性权重ω计算如下:

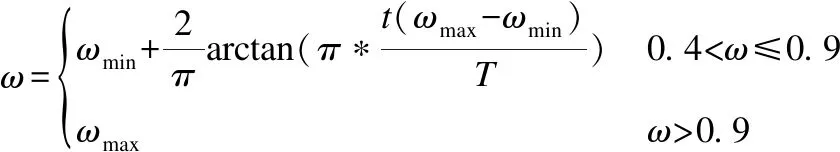
(5)

其中t和T分别代表迭代次数和最大迭代次数,取ωmax=0.9,ωmin=0.4时曲线如图1所示:

图1曲线表明,随着迭代次数的增加,惯性权重呈现非线性递增状态,可以知道改进后的算法在寻优早期有较小的w,具有较强的局部探索能力;在寻优后期具有较大的w,具有较强的全局探索能力.

3.2 变异算子

由于变异算子在提升算法收敛性能方面有着显著表现,因此本文在借鉴遗传算法变异思想的基础上,结合文献[14],将变异算子融入二进制粒子群优化算法中,防止算法出现早熟收敛的现象.对二进制粒子群改进公式如下:

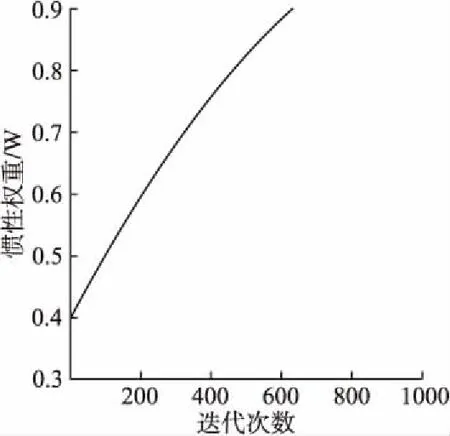
图1 惯性权重变化曲线Fig.1 Inertia weight change curve

(6)

其中,Random为解空间随机位置;ρ为对未知世界的好奇系数,经过大量实验观察,设置ρ=2可以得到最好的效果,r3是分布在[0,1]内的随机数.由于加入了对未知空间探索的机制,不仅使粒子寻优范围得到扩大,种群多样性得到增强,而且使算法更易于跳出局部最优,从而防止算法的早熟收敛.

3.3 MABPSO算法步骤

MABPSO算法从惯性权重和变异算子两个角度对BPSO进行了优化,步骤如下:

Step 1.初始化MABPSO算法的粒子速度、位置、个体与全局极值等参数.

Step 2.计算粒子适应度值.

Step 3.粒子根据适应度值,更新个体最优和全局最优

Step 4.根据公式(5)对惯性权重更新.

Step 5.通过公式(6)和公式(3)实现粒子速度和位置更新

Step 6.若算法达到终止条件,则输出最优值,否则返回到步骤2.

4 实验结果分析

4.1 实验设计

为了验证本文提出的MABPSO算法的优化性能,分别在三个单峰Sphere、Step、Rosenbrock函数和三个复杂的多峰Rastrigin、Ackley、Griewank函数进行测试.并利用惯性权重线性递减的二进制粒子群优化算法(BPSO)[5]、惯性权重线性增大的二进制粒子群优化算法(UPBPSO)[13]和结合本文提出的带未知空间探索变异算子的二进制粒子群优化算法(MBPSO)进行对比.测试函数参数如表1所示.

算法参数设置如下:4种算法最大迭代次数为1000,种群规模为30,在300维情况下运行.4个算法BPSO、UPBPSO、MBPSO、MABPSO中,惯性权重初始值ω为2,最大值ωmax为0.9,最小值ωmin为0.4,c1、c2值为2,MABPSO算法中ρ值设置为2.

表1 测试函数
Table 1 Test function

函数名称表达式极值Sphere(F1)F1(x)=∑Di=1x2i0Step(F2)F2(x)=∑Di=1(xi+0.5)20Ackley(F3)F3(x)=-20exp-0.21D∑Di=1x2i()-exp1D∑Di=1cos(2πxi)()+20+e0Rastrigin(F4)F4(x)=∑Di=1[x2i-10cos(2πxi)+10]0Griewank(F5)F5(x)=1400∑Di=1x2i-∏Di=1cosxii+10Rosenbrock(F6)F6(x)=∑Di=1(1-xi)2+100(xi+1-x2)20

实验中对算法性能的评价标准如下:

1)均值:算法运行n次得到最优解结果的均值.

2)方差:算法执行n次得到最优解结果的方差.

3)最优值:算法执行n次后,n个最优值中最好的一个.

4)最劣值:算法执行n次后,n个最优值中最差的一个.

为使测试结果更加公平,所有测试均采用Inter Core i5 2.3G双核处理器,16G内存,MacOS操作系统,Matlab2014b仿真环境.

4.2 实验结果分析

4种算法在300维情况下对每个测试函数独立运行30次,分别保存最好值、最差值、平均值和标准差,实验结果如表2所示.

单峰函数只有一个全局最优解而没有局部最优解,适合检测算法的收敛精度.从表2中可以看出,在单峰函数F1、F2、F6中,MBPSO所得最优值、最劣值、均值均好于BPSO和UPBPSO算法,说明MBPSO的收敛精度高于BPSO和UPBPSO算法,同时MABPSO的最好值、最差值、均值均好于MBPSO,说明MABPSO的收敛精度高于MBPSO,并且是4个算法中最好的.

表2 测试函数为300维时数据
Table 2 Test function is 300-dimensional data

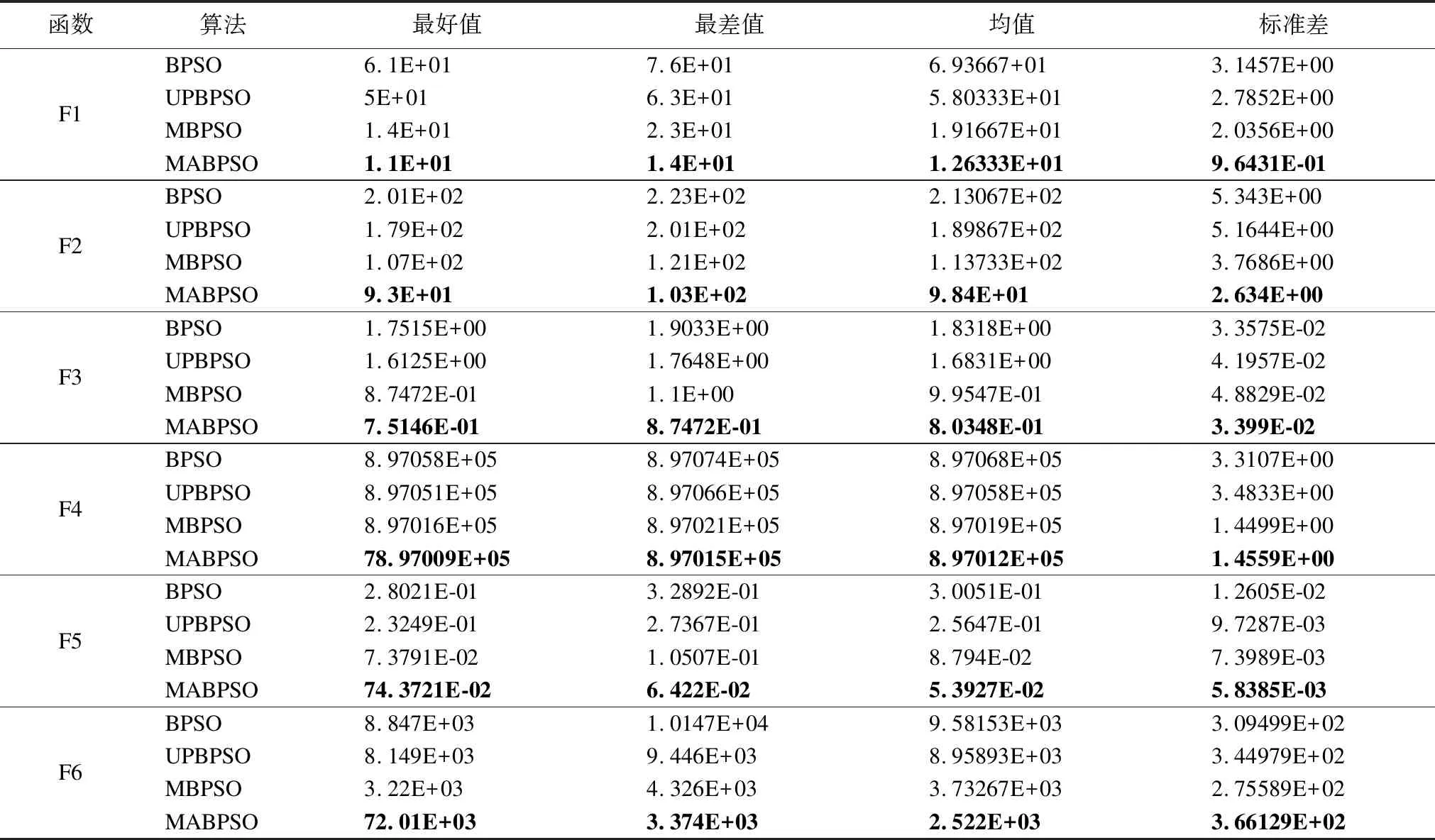
函数算法最好值最差值均值标准差F1BPSO6.1E+017.6E+016.93667+013.1457E+00UPBPSO5E+016.3E+015.80333E+012.7852E+00MBPSO1.4E+012.3E+011.91667E+012.0356E+00MABPSO1.1E+011.4E+011.26333E+019.6431E-01F2BPSO2.01E+022.23E+022.13067E+025.343E+00UPBPSO1.79E+022.01E+021.89867E+025.1644E+00MBPSO1.07E+021.21E+021.13733E+023.7686E+00MABPSO9.3E+011.03E+029.84E+012.634E+00F3BPSO1.7515E+001.9033E+001.8318E+003.3575E-02UPBPSO1.6125E+001.7648E+001.6831E+004.1957E-02MBPSO8.7472E-011.1E+009.9547E-014.8829E-02MABPSO7.5146E-018.7472E-018.0348E-013.399E-02F4BPSO8.97058E+058.97074E+058.97068E+053.3107E+00UPBPSO8.97051E+058.97066E+058.97058E+053.4833E+00MBPSO8.97016E+058.97021E+058.97019E+051.4499E+00MABPSO78.97009E+058.97015E+058.97012E+051.4559E+00F5BPSO2.8021E-013.2892E-013.0051E-011.2605E-02UPBPSO2.3249E-012.7367E-012.5647E-019.7287E-03MBPSO7.3791E-021.0507E-018.794E-027.3989E-03MABPSO74.3721E-026.422E-025.3927E-025.8385E-03F6BPSO8.847E+031.0147E+049.58153E+033.09499E+02UPBPSO8.149E+039.446E+038.95893E+033.44979E+02MBPSO3.22E+034.326E+033.73267E+032.75589E+02MABPSO72.01E+033.374E+032.522E+033.66129E+02

多峰函数具有多个局部最优解且随问题维度的增加成指数增加,适合检测算法避免陷入局部最优解的能力.从表2中可以看出,在多峰函数F3、F4、F5中,MBPSO所得最好值、最差值、均值均好于BPSO和UPBPSO算法,说明MBPSO避免陷入局部最优解的能力强于BPSO和UPBPSO,同时MABPSO在所有测试函数上的最好值、最差值、均值均好于MBPSO,说明MABPSO避免陷入局部最优解的能力强于MBPSO,并且是四个算法中最好的.

无论是多峰函数还是单峰函数,MBPSO所得最好值、最差值、均值均好于BPSO和UPBPSO算法,说明未知空间探索的变异算子对速度公式的改进使粒子探索范围得到扩大,逃离局部解的能力得到加强;同时MABPSO在所有测试函数上的最好值、最差值、均值均好于MBPSO,说明惯性权重值的非线性增长,更好的平衡了算法全局探索与局部开采的性能,较大提升了算法收敛效率.在F1、F2、F5上,MABPSO有最好的标准差,在F3、F4、F6上,MABPSO的标准差比BPSO和MBPSO略大,但差别很小,说明MABPSO算法在提升收敛精度和增强算法跳出局部最优解能力的同时,没有破坏算法的稳定性.

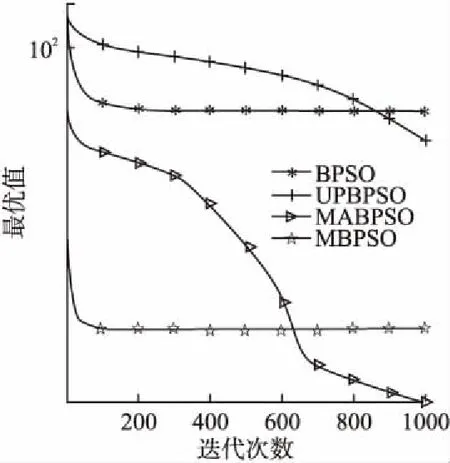
图2 函数F1收敛曲线图Fig.2 Function F1 convergence curve

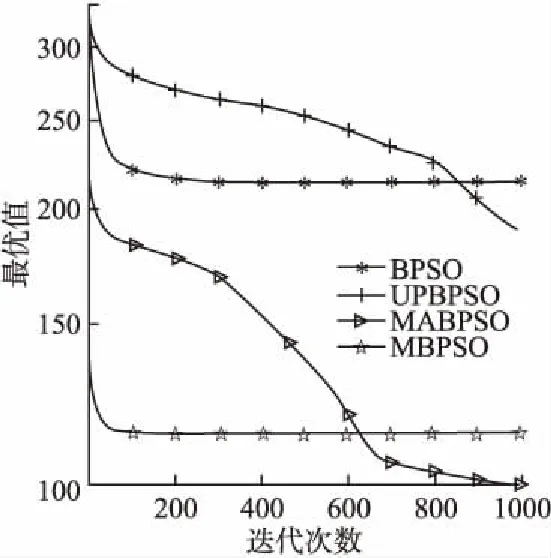
图3 函数F2收敛曲线图Fig.3 Function F2 convergence curve

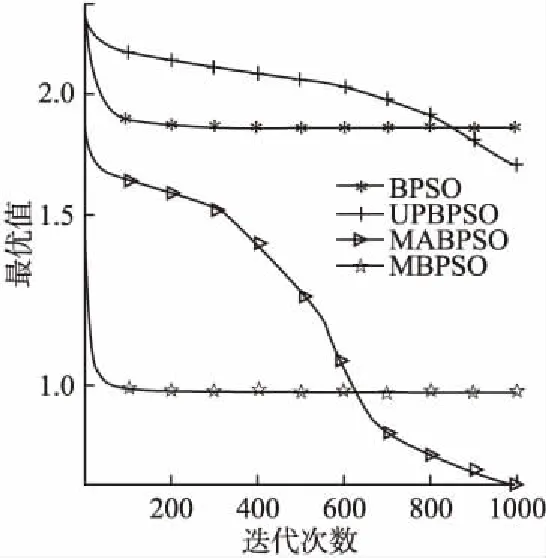
图4 函数F3收敛曲线图Fig.4 Function F3 convergence curve

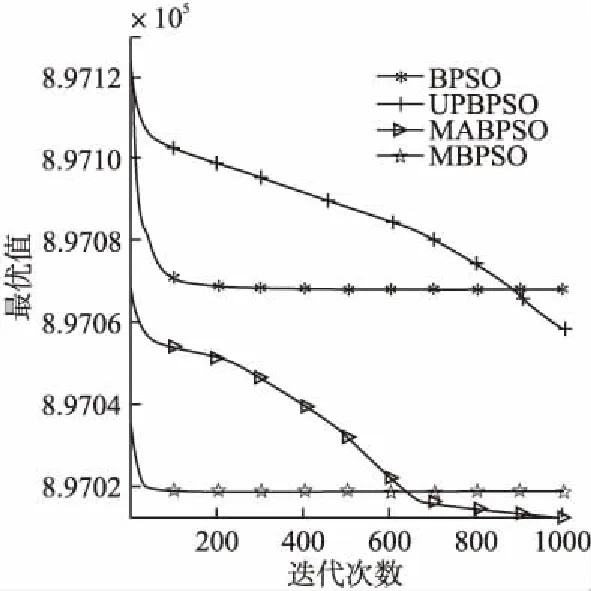
图5 函数F4收敛曲线图Fig.5 Function F4 convergence curve

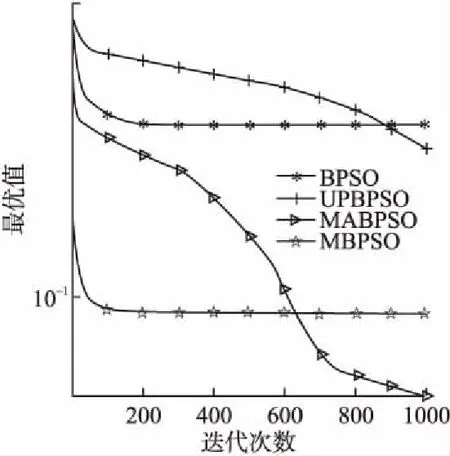
图6 函数F5收敛曲线图Fig.6 Function F5 convergence curve

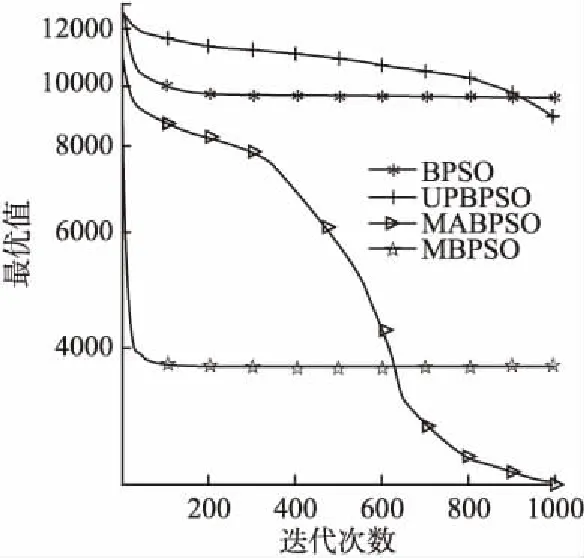
图7 函数F6收敛曲线图Fig.7 Function F6 convergence curve

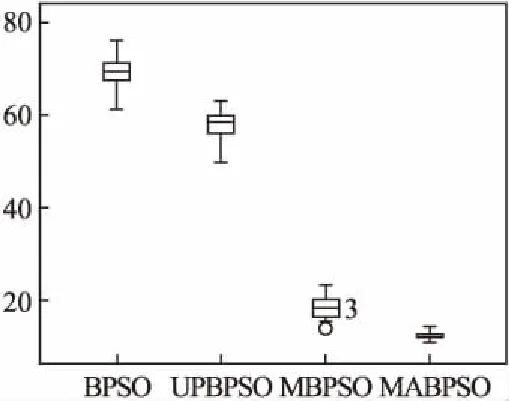
图8 函数F1箱须图Fig.8 Function F1 box whisker

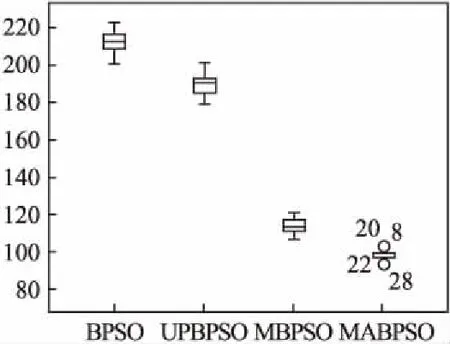
图9 函数F2箱须图Fig.9 Function F2 box whisker

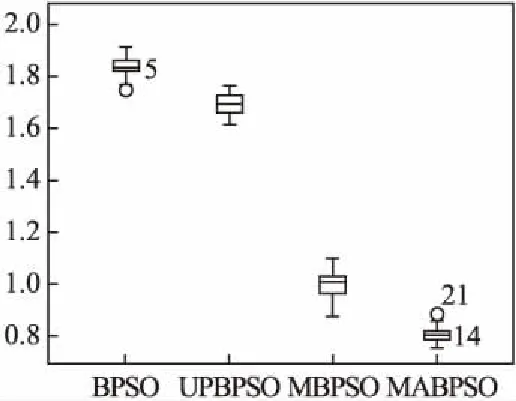
图10 函数F3箱须图Fig.10 Function F3 box whisker

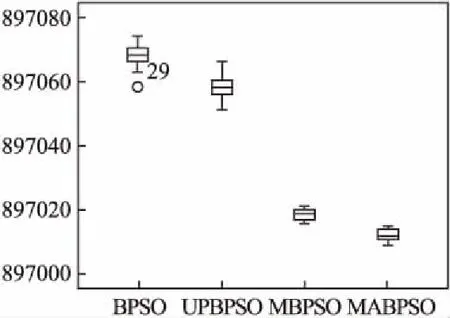
图11 函数F4箱须图Fig.11 Function F4 box whisker

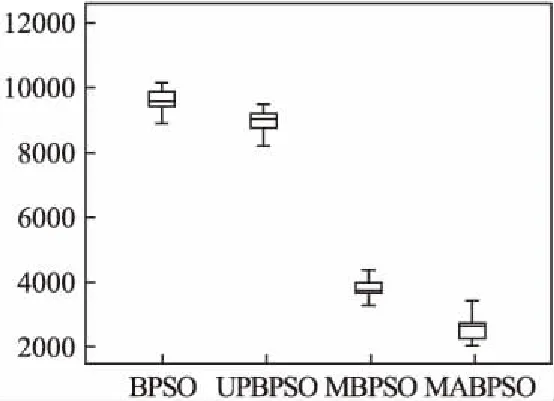
图13 函数F6箱须图Fig.13 Function F6 box whisker

算法的收敛图可以清楚的表明各个算法的寻优过程.图2-图7分别表示4个算法在维数D=300时,在6个测试函数上独立运行30次的平均收敛曲线.从图中可以看出,在F1、F2、F3、F4、F5、F6上,BPSO算法的最终收敛精度劣于UPBPSO算法;向基本的BPSO算法加入变异算子设计的MBPSO相比BPSO算法、UPBPSO算法,收敛速度和收敛精度显著提高,说明加入未知空间探索的变异算子,扩大了粒子的搜索范围,增强了粒子的种群多样性,极大提高了算法的收敛速度和收敛精度;但是在跳出局部最优值方面的能力还有所欠缺.从图中可知,融合变异算子和自适应惯性权重的MABPSO算法比其他3种算法不易陷入局部最优,收敛精度上也更加精确,说明自适应调整的惯性权重平衡了算法的全局搜索和局部搜索,惯性权重的非线性递增变化比线性递增变化更符合粒子的运动规律,进一步提高了算法的性能.

为了更加直观看出解集分布情况,给出了4种算法在6个测试函数上的解集箱须图,如图8-图13所示.

从图8-图13所示中可以看出,在F1、F2、F6三个单峰函数中,MABPSO算法得到的数据整体都比其他算法得到的数据更加接近横坐标轴,说明数据MABPSO算法得到的解优于对比算法.在Sphere函数和Step函数上,数据MABPSO算法得到的数据范围小于对比算法,说明MABPSO更加具有较好的稳定性.在F3、F4、F5三个多峰函数上,MABPSO算法得到的数据同样更加接近横坐标轴,得到的数据范围也小于对比算法,说明MABPSO算法不仅具有较好的收敛性能,而且具有较好的稳定性.因此,本文提出的MABPSO算法不管是在简单的单峰函数,还是在较复杂的多峰函数上都具有较好的收敛表现.

5 结 论

为改善二进制粒子群优化算法在寻优过程中收敛速度慢、搜索精度不高和易陷入局部最优而无法取得全局最优解的问题,本文提出惯性权重非线性递增的改进策略,该策略平衡了二进制粒子群算法的全局探索与局部开采性能.同时,引入对未知空间搜索的变异算子对BPSO算法进行改进,提高了算法的执行速度,增强了种群多样性,进而大幅度加强了算法避免陷入局部最优的能力,从整体上提高了算法的收敛速度和收敛精度.仿真实验结果表明,本文提出的带变异算子的自适应惯性权重二进制粒子群优化算法与其它算法相比,收敛速度更快,收敛精度更高,是一种优化能力强,稳定性好的全局优化算法.