矩形法兰孔孔口模态辐射阻抗的计算与分析∗

李家柱 叶望青 钟秤平 陈 剑 刘 策

(1 合肥工业大学机械工程学院噪声振动工程研究所 合肥 230009)

(2 安徽省汽车NVH 工程技术研究中心 合肥 230009)

(3 江西省汽车噪声与振动重点实验室 南昌 330001)

0 引言

孔口模态辐射阻抗的计算是矩形法兰孔声传递损失(Transmission loss, TL)计算的基础，是开展大尺寸百叶窗隔声量计算的关键环节。大尺寸百叶窗结构在建筑物外立面、暖通系统以及高铁减载式声屏障等领域应用广泛。矩形法兰孔孔口模态辐射阻抗表达式是包含半空间格林函数和两组模态振型的四重积分，该积分存在奇异点，现有的高阶积分算法和计算软件无法直接求解[1]。对于这类问题，多数学者通过坐标变换将积分降为三重或二重积分，然后采用高斯求积来求解[2−5]。这种方法实现了积分的精确求解，但在积分变换后，表达式需根据相应的阶次进行讨论，且高斯求积方法虽较成熟，但并非MATLAB 等软件的内置函数，仍需编写高斯求积程序。Sha 等[1]则在将四重积分降为二重积分后，将结构划分为网格，利用边界条件、波数近似和傅里叶变换等方法来加速求解模态辐射阻抗，该方法需根据结构的尺寸、波数等参数改变网格大小，计算过程较复杂且计算速度不够理想。Li 等[6−7]、沈苏等[8]和Leppington 等[9]等通过坐标变换、参数讨论等方法将这类积分降为一重积分，简化了积分最终的求解表达式并提高了计算速度。Davy等[10]在将四重积分降为一重积分的基础上，通过改写最终表达式消除了奇异积分的影响。然而，这类将四重积分降为一重积分的方法推导过程复杂且需进行参数讨论，如果初始的模态辐射阻抗表达式与文献中的表达式有差异，就需重新推导，对理论知识要求较高且工作量大。

鉴于此，本文在吸收以上学者成果的基础上，通过坐标变换将四重积分转换为二重积分并消除奇异积分，且将该过程直接采用MATLAB 的内置函数来实现。在实现四重积分求解的基础上，通过详细计算和对比，验证方法的正确性，最后分析矩形法兰孔孔口模态辐射阻抗的性质。

1 矩形法兰孔孔口模态辐射阻抗计算

1.1 矩形法兰孔孔口模态辐射阻抗表达式

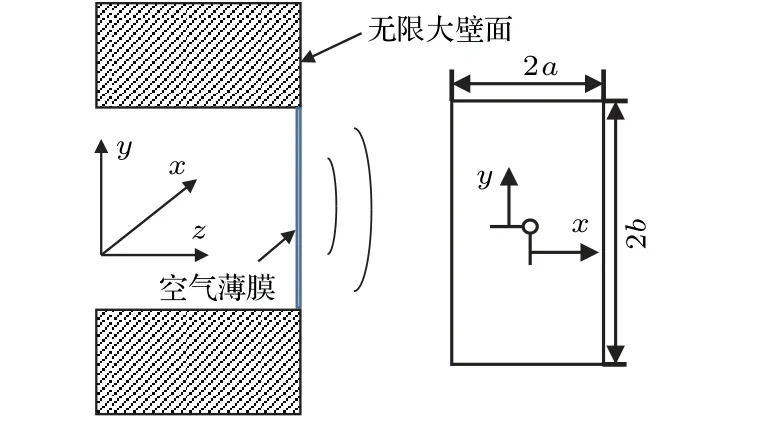
图1 矩形法兰孔示意图Fig.1 Schematic diagram of flanged rectangular aperture

声源表面的声压与振速的比值称为声源的辐射阻抗[11]。图1为矩形法兰孔示意图，该孔孔口处为无限大壁面形成的半空间，孔口的振动单元可视为空气薄膜，由于受孔口约束，空气薄膜的四边仅有图1所示的z向平动自由度，其振动模态对应孔口截面模态。空气薄膜各阶振动模态对应的辐射阻抗即为矩形法兰孔孔口模态辐射阻抗，其表达式为[5]

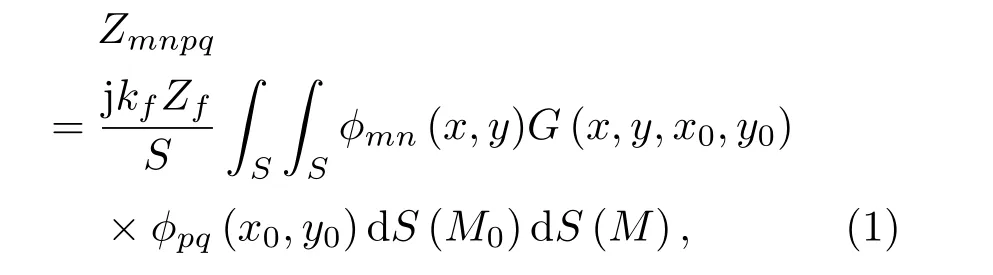
式(1)中，j为虚数单位，kf和Zf分别为波数和声传播介质的特征阻抗，本文以空气为声传播介质，则Zf为空气的特征阻抗，ϕmn(x,y)和ϕpq(x0,y0) 分别为空气薄膜的(m,n)和(p,q)阶模态的振型，表达式分别为

G(x,y,x0,y0)为半空间格林函数，其表达式为

将 式(2)∼(4)以 及S= 4ab代 入 式(1)可 得(m,n,p,q)阶模态辐射阻抗表达式为

1.2 积分变换

式(5)是以x0、y0、x、y为积分变量的四重积分，积分区间分别为(−a,a)、(−b,b)、(−a,a)、(−b,b)，在x=x0且y=y0处，积分函数趋于无穷大，无法直接计算。为求解该积分，采用换元法，令

可得

雅可比矩阵为

同理，Jy=1/2，此时式(5)变换为

式(9)中：

式(10)∼(13)均可对ζ和γ积出解析表达式，式(9)将被转换为四个以κ和τ为积分变量的二重积分之和。然而，当κ和τ趋于零时依然会造成积分中格林函数分母趋于零，该积分存在奇异性，需做一次极坐标变换，令：

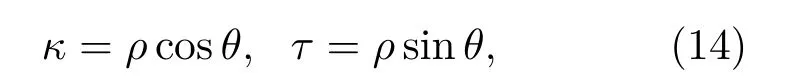
变换后的式(9)被转换为极坐标下的二重积分，该积分可直接使用MATLAB内置的数值积分函数求解，无需采用高斯求积或对模态阶次进行讨论。

1.3 MATLAB求解

第1.2 节所述过程可在MATLAB中完成，主要有以下几步：

(1) 根据式(2)∼(4)，在MATLAB 中定义模态振型函数ϕmn(x,y)、ϕpq(x0,y0)以及半空间格林函数G(x,y,x0,y0)。

(2) 将变量代换式(7)带入第(1)步定义的函数，得到变量代换后的模态振型表达式和半空间格林函数表达式。

(3) 将变量代换后的模态振型和半空间格林函数表达式代入式(5)，即得到新的模态辐射阻抗表达式(9)，要对式(9)求解，需分别对式(10)∼(13)求定积分。

(4) 在MATLAB 中 采 用int 函 数 对 式(10)∼(13)中的变量ζ和γ求定积分，将式(10)∼(13)由四重积分转换为仅含变量κ和τ的二重积分，此步在MATLAB中可积出解析表达式。

(5) 降维后的式(10)∼(13)由于包含半空间格林函数而存在奇异性，此时在MATLAB 中根据式(14)进行极坐标变换，消除奇异积分，得到极坐标下的积分表达式。

(6) 最后利用MATLAB积分函数quad2d分别对降维和极坐标变换后的式(10)∼(13)求数值积分，将式(10)∼(13)求解结果代入式(9)即可求得矩形法兰孔孔口模态辐射阻抗。

2 计算结果验证

2.1 (0,0,0,0)阶模态辐射阻抗验证

矩形法兰孔孔口的(0,0,0,0)阶模态辐射阻抗就是矩形活塞声源的辐射阻抗，矩形活塞声源辐射阻抗表达式和相关计算数据可在文献[12]中查阅。如图2所示，法兰孔孔口尺寸为长宽均为1 m 的正方形，图2中Z(0,0,0,0)为(0,0,0,0)阶模态辐射阻抗，Z0为空气的特征阻抗，Z(0,0,0,0)/Z0为归一化的模态辐射阻抗，k为波数，req为等效半径由图2可知，本方法算得的(0,0,0,0)阶模态辐射阻抗与矩形活塞声源辐射阻抗实部和虚部一致性很好，说明本方法计算(0,0,0,0)阶模态辐射阻抗是正确的。

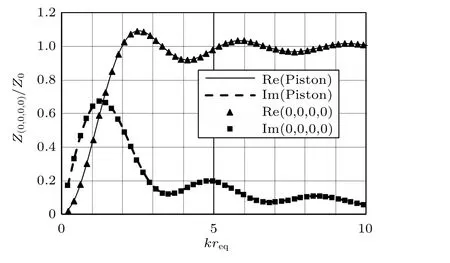
图2 (0,0,0,0)阶模态辐射阻抗验证Fig.2 Radiation impedance validation of order(0,0,0,0)

2.2 高阶模态辐射阻抗验证

由于高阶模态辐射阻抗难以通过仿真或实验直接得到，因此本文将模态辐射阻抗计算方法代入矩形法兰孔声传递损失计算中来。通过代入本文阻抗计算方法的Superposition 法与Sgard 等[5]、声学有限元法以及实验[13]的对比，间接验证本方法的正确性。

矩形法兰孔的声传递率与其孔口模态辐射阻抗的关系为[13]

式(15)中，Zmnmn为孔口第(m,n,m,n)阶模态辐射阻抗，该式已利用本文的结论之一：互模态辐射阻抗相比于自模态辐射阻抗在多数计算中可以忽略不计的性质进行了简化，只计算了自模态辐射阻抗部分。关于孔口模态辐射阻抗性质的分析将在本文后续小节中加以论述。

声传递损失与声传递率的关系为[13]从而可以根据式(16)求得矩形法兰孔的声传递损失，式(15)和式(16)中部分参数的具体描述请见参考文献[13]。

图3和图4对比了代入本文阻抗计算方法的Superposition法[13]和Sgard等[5]方法的计算结果，矩形孔尺寸均为Lx=0.4 m，Ly=0.2 m，Lz=0.3 m。图3为法向入射时的声传递损失，图4是入射角度为斜45◦时的声传递损失。图3中Sgard 等的数据为采用其论文中的算法计算得到，经对比二者几乎相等。图4中Sgard 等的数据为直接从其论文的图中提取出来，略微存在一定误差，这主要是提取数据的误差造成的。

图3 法向入射条件下矩形孔声传递损失验证Fig.3 TL validation of a rectangular aperture with normal incident

图4 倾斜入射条件下矩形孔声传递损失验证Fig.4 TL validation of a rectangular aperture with oblique incident

图5为散射声场中代入本文阻抗计算方法的Superposition 法[13]、Trompette 等[14]的实验以及声学有限元法的对比，矩形孔尺寸为Lx=0.06 m，Ly=0.13 m，Lz=0.3 m。观察图5可知，三条曲线一致性较好。

以上通过将本文模态辐射阻抗计算方法代入Superposition 法， 与Sgard 等的计算结果、Trompette 等的实验结果以及声学有限元法的结果对比，取得了很好的一致性，从侧面验证了本方法计算高阶模态辐射阻抗的正确性。

图5 散射声场中矩形孔声传递损失对比Fig.5 TL validation of a rectangular aperture in diffuse acoustic field

3 计算结果分析

3.1 自模态辐射阻抗分析

当式(1)中m=p或n=q时的模态辐射阻抗称为自模态辐射阻抗，图6和图7为孔口边长为1 m的正方形法兰孔孔口的前7 阶自模态辐射阻抗实部和虚部的对比。

观察图6和图7，可得如下结论：

(1)随着模态阶次的增加，自模态辐射阻和自模态辐射抗的峰值总体呈减小趋势，但不是单调递减的，高阶次的峰值可能高于低阶次的峰值。

(2)随着模态阶次的增加，自模态辐射阻和自模态辐射抗的峰值对应的kreq均逐渐增大，由于req为等效半径，为常数，即对应的波数k增大，亦即对应的频率逐渐增大。

图6 自模态辐射阻对比(Lx = 1 m、Ly = 1 m)Fig.6 Resistance comparison of self-modal radiation impedance(Lx = 1 m、Ly = 1 m)

图7 自模态辐射抗对比(Lx =1 m、Ly =1 m)Fig.7 Reactance comparison of self-modal radiation impedance(Lx =1 m、Ly =1 m)

图8 自模态辐射阻对比(Lx = 0.5 m、Ly = 1 m)Fig.8 Resistance comparison of self-modal radiation impedance(Lx = 0.5 m、Ly = 1 m)

图9 自模态辐射抗对比(Lx = 0.5 m、Ly = 1 m)Fig.9 Reactance comparison of self-modal radiation impedance(Lx = 0.5 m、Ly = 1 m)

(3)孔口形状为正方形时，由于对称性，(m,n,m,n)与(n,m,n,m) 阶自模态辐射阻和自模态辐射抗相等。

进一步，选取孔口边长分别为Lx= 0.5 m、Ly=1 m的矩形法兰孔，计算其孔口模态辐射阻抗并分析其规律。

观察图8和图9，并结合图6和图7可知，当法兰孔孔口形状为长方形时，其模态辐射阻抗的性质与孔口形状为正方形时相似。不同之处在于，其不具有(m,n,m,n)与(n,m,n,m)阶模态辐射阻和模态辐射抗相等的对称性，是因为长方形的边长不相等。

3.2 互模态辐射阻抗分析

(1)四个阶次的互模态辐射阻和辐射抗的峰值相比于自模态辐射阻和辐射抗的峰值均小很多，峰值最大的(1,2,3,4)阶互模态辐射阻抗也比自模态辐射阻抗小1∼2个数量级。

(2)由图10、 图11 和表1可知， 另三阶比(1,2,3,4)阶模态辐射阻抗小多个数量级。

图10 互模态辐射阻对比(Lx = 0.5 m、Ly = 1 m)Fig.10 Resistance comparison of cross-modal radiation impedance(Lx = 0.5 m、Ly = 1 m)

图11 互模态辐射抗对比(Lx = 0.5 m、Ly = 1 m)Fig.11 Reactance comparison of cross-modal radiation impedance(Lx = 0.5 m、Ly = 1 m)

表1 互模态辐射阻抗对比Table1 Comparison of cross-modal radiation impedance

4 结论

论文详细阐述了矩形法兰孔孔口模态辐射阻抗积分表达式坐标变换的过程及其在MATLAB中的实现方法，对计算结果进行了验证并分析了模态辐射阻抗的性质，结论如下：

(1)通过坐标变换将四重积分转换为二重积分并消除了奇异积分，且将计算过程直接利用MATLAB 软件的内置函数实现，不再需要推导公式且不再需要根据模态阶次讨论模态辐射阻抗的具体表达式，显著降低了积分求解的复杂程度。

(2)随着模态阶次的增加，自模态辐射阻抗峰值总体呈减小趋势但并非单调递减，峰值对应的频率逐渐增大。

(3)自模态辐射阻抗显著大于互模态辐射阻抗，往往相差多个数量级，结合实际情况可只计算自模态辐射阻抗部分，以显著降低计算工作量、提高计算速度。