一种改进的非整数自适应时延估计方法∗
李均浩 刘文红
(1 上海电机学院电气学院 上海 201306)
(2 上海电机学院电子信息学院 上海 201306)
0 引言
机电设备故障诊断有许多种方法,故障声故障定位能够不接触设备,通过采集设备的声场信息和阵列处理技术,确定声源的位置,直观地找到故障源,进而查明故障的原因,例如变速箱噪声控制[1]、空调压缩机异常声定位[2]和风机气动噪声源定位[3]。声源定位系统是微型、独立且可移植的,对于大型设备检测系统复杂的情况,可以从某些故障具有发声的特征运用声源定位技术补充设备故障诊断系统[4]。基于时延估计的声源定位中,时延估计算法性能对定位的效果有直接的影响。文献[5]对空调外机故障声和背景噪声进行分析建模,故障声信号的低信噪比和脉冲噪声的影响要求时延估计算法能够处理这些状况。
相关法时延估计是运用最广泛的算法。文献[6]对二次相关法进行改进,锐化峰值位置,时延估计效果好于二次相关法和相关法。文献[7]进行二次相关算法后,对相关峰值由希尔伯特差分法进一步改善。文献[8]通过实验对比相关、共变、分数低阶协方差算法,证明分数低阶算法更具有鲁棒性。文献[9]提出共变相关算法,能够抑制脉冲噪声,低信噪比下估计精度高于共变法和相关法。相关法只能对时延估计值整数位进行估计,对一些低频故障声源[10]进行定位,若采样频率只满足采样定理,分数位的误差对定位影响很大;提高信号的采样率能够提高时延估计的分辨率,但相关峰值就不尖锐,不易找到峰值的位置;同时提高采样率在硬件实现上亦增加了难度。
提高时延估计分辨率有两种方法,一种方法是插值,另一种方法是直接估计出非整数时延。文献[11]首先用相关法求时延估计值,然后用sinc 函数对一个序列进行时延处理,时延值为采样周期的一定百分比,再进行相关运算,与之前的峰值进行比较,得到更精确的时延估计值;若要提高分辨率,则要在此前基础上重复这一过程,分辨率仍然受影响。文献[12]用时延估计方法对电站锅炉进行高温测量,基于背景噪声非常接近高斯过程时,为了克服在低时变信噪比下估计电站锅炉内精确时间延迟的困难,研究了基于四阶累积量的显式时延增益估计算法。文献[13]提出一种基于最小平均p范数的非整数自适应时间延迟估计方法,称为LMPFTDE算法,在高斯噪声和脉冲噪声环境都具有良好的鲁棒性,算法的代价函数为多峰函数,但时延值在D −0.5 与D+0.5 之间(D为时延真值),代价函数是单峰的,需要其他算法对时延估计值先进行整数位的准确估计,作为迭代初始值来估计非整数的时延真值。
在满足采样定理的采样率下,考虑故障信号的低信噪比和噪声含有脉冲信号的特点,本文通过两步对时延估计值进行更准确的估计。首先将观测序列进行自共变和互共变运算,将共变序列进行相关法时延估计,得到时延估计值的整数位,作为非整数自适应时延估计算法的初始值;然后将共变序列作为LMPFTDE算法的输入信号,实现在低采样率下对时延估计值更加准确的估计。
1 α稳定分布和共变
1.1 α稳定分布
α稳定分布是一种广义的高斯模型[14],根据广义中心极限定理,它是唯一的一类构成独立同分布随机变量之和的极限分布,高斯分布是其子类。高斯分布和α稳定分布的区别在于:高斯分布具有指数拖尾,α稳定分布具有代数拖尾。所以α稳定分布能够更好地描述噪声中的脉冲过程。
除少数几种情况外,α稳定分布的概率密度函数没有解析的表达式。特征函数和概率密度函数是互相唯一确定的关系,特征函数本质上是概率密度函数的傅里叶逆变换,它们都可以完全描述一个随机分布的统计特性,下面是α稳态分布的特征函数介绍。
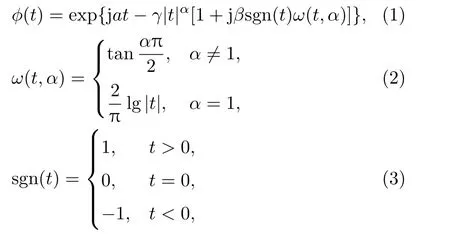
则随机变量X服从α稳定分布。
式(1)中参数α为特征指数,它决定α稳定分布的脉冲性程度。α值越小,所对应分布的拖尾越厚,样本的脉冲性越显著;反之,α值变大,所对应分布的拖尾变薄,样本的脉冲性减弱。当α= 2 时,α分布对应高斯分布,α稳态分布是广义的高斯分布。参数β确定分布的斜度,γ是分散系数,它是样本相对于均值分散程度的度量,a为位置参数,对应α稳定分布的中值或均值。
1.2 共变
共变[15]是一种分数低阶统计量(Fractional lower order statistics, FLOS),它在SαS分布(对称α稳定分布)随机变量中的作用类似于协方差在高斯分布随机变量中的作用。两个满足的联合SαS分布随机变量x和y,其共变定义为
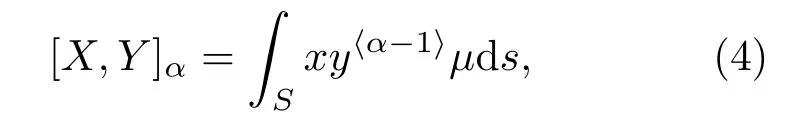
式(4)中,S表示单位圆;µ(◦)表示SαS分布随机向量(x,y)的谱测度;由于谱测度µ(◦)不易得到,因此,实际中常常通过分数低阶距(Fractional lower order moment,FLOM)来获得共变。两个满足的联合SαS分布随机变量x和y,其共变与FLOM具有如下的关系:
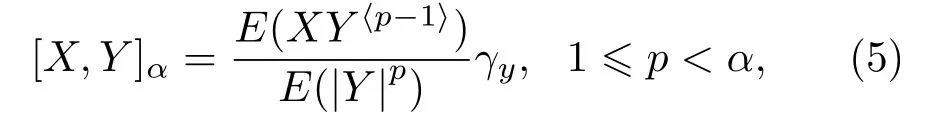
式(5)中,γy为随机变量y的分散系数。
共变具有的一些性质[15]在α稳定信号处理和分析中起着重要的作用。
性质1 共变[X,Y]α对第一变元x是线性的,即如果x1、x2和y服从联合SαS,

式(6)中,A和B为任意实数。
性质2 如果y1和y2是独立的,且x、y1和y2服从联合SαS,则
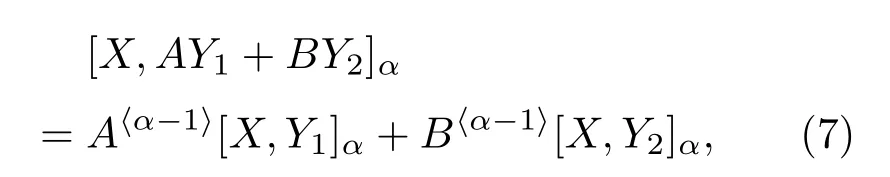
式(7)中,A和B为任意实数。
性质3 如果x和y是独立的且服从联合SαS,则[X,Y]α= 0。反之,通常是不成立的。当α= 2时,即x和y服从零均值的联合高斯分布时,x和y的共变就退化为x和y的协方差,
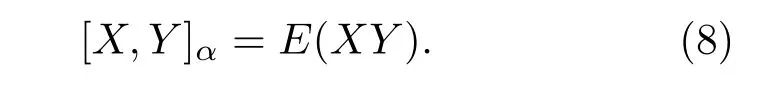
2 算法分析
2.1 信号噪声模型
假定两个接收信号x1(n)和x2(n)满足下面的离散信号模型:
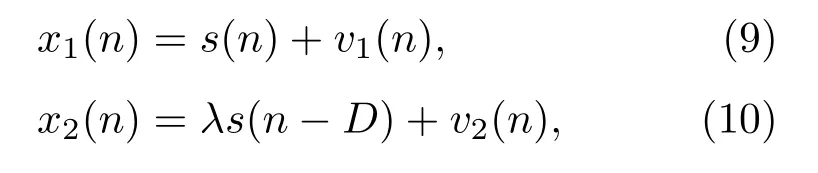
其中,λs(n −D)为相对于s(n)的延迟源信号,λ为衰减因子(为了简便通常取λ= 1),v1(n)、v2(n)分别为两个接收端接收到的背景噪声,服从α稳定分布。假定信号与噪声、噪声与噪声是统计独立的。
2.2 共变相关算法
互共变[x1(n),x2(n)]p−1和自共变[x1(n),x1(n)]p−1可以写为
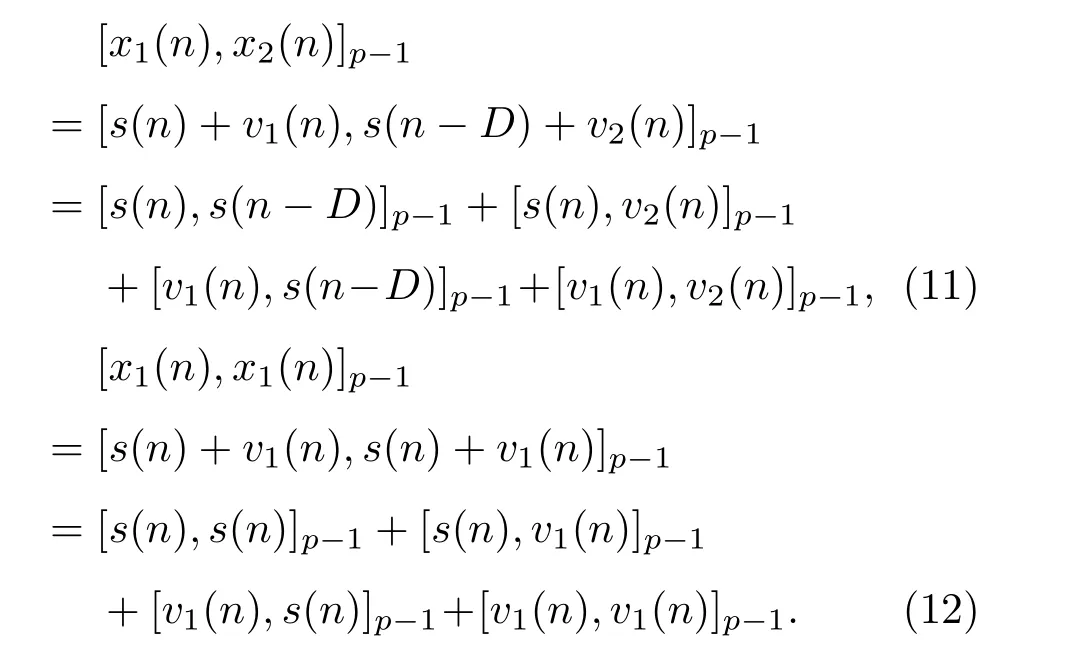
由于假定了信号s(n)和噪声v1(n)、v2(n)是统计独立的,依据共变的性质,
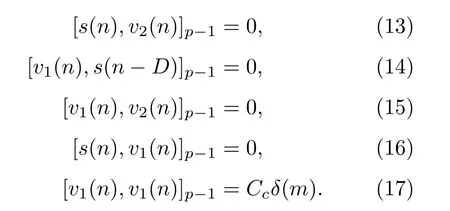
式(10)和式(11)可以化简为

因此,x1(n)和x2(n)的互共变Rc12(m),x1(n)的自共变Rc11(m)分别为

原始序列经过自共变和互共变后,自共变序列可以看作是互共变序列经过移位并加入一个干扰Ccδ(m)而得到的,共变序列保留了原始序列的相位信息,削弱了不相干噪声干扰,提高信噪比,但在处理数据有限的情况下,干扰噪声不会为零。经共变处理的原始数据进行互相关时延估计的估计效果在相同信噪比和脉冲环境要好于直接进行互相关法和共变法[9]。
2.3 LMPFTDE算法
LMPFTDE 算法[13]用一个系数为sinc 采样函数的滤波器来拟合时间延迟,可以直接对时间延迟真值为非整数采样间隔的情况进行估计。在实际应用中,信号和噪声的统计特性以及信噪比等都有可能随时间变化,自适应滤波器的权系数是输入信噪比与时间延迟真值的二元函数。考虑时间延迟和信噪比两个因素来进行滤波器权系数的修正,将滤波器分为两级级联,一级用于适应信噪比的变化,另一级用于跟踪时间延迟,则可以将时间延迟和信噪比的自适应过程解耦,从而改善时间延迟估计的性能。输出误差e(n)在n时刻为
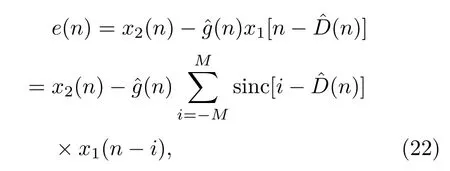
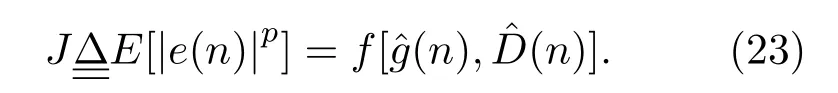
这是一个二维的非线性优化问题,运用松弛法,将其解耦转化为两个一维的优化问题,分别对增益和时间延时进行迭代,以求得最优解,在一定的时间延迟范围内,代价函数J为单峰函数,有唯一的最小值,故采用最速下降法,利用梯度技术,并以误差信号的瞬时值代替统计平均。自适应迭代公式为

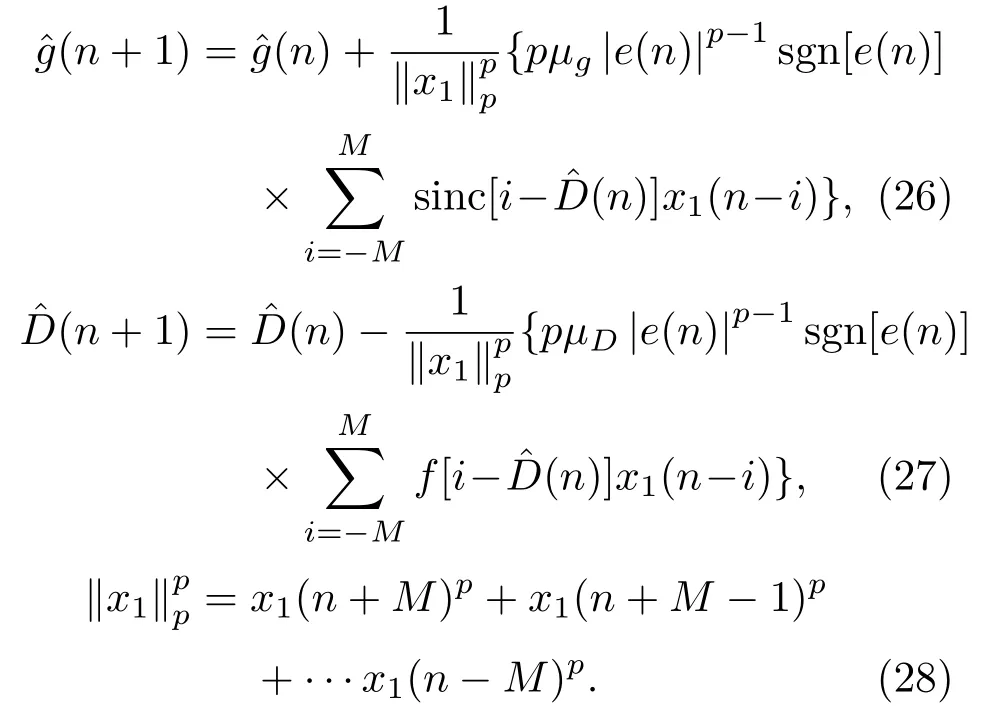
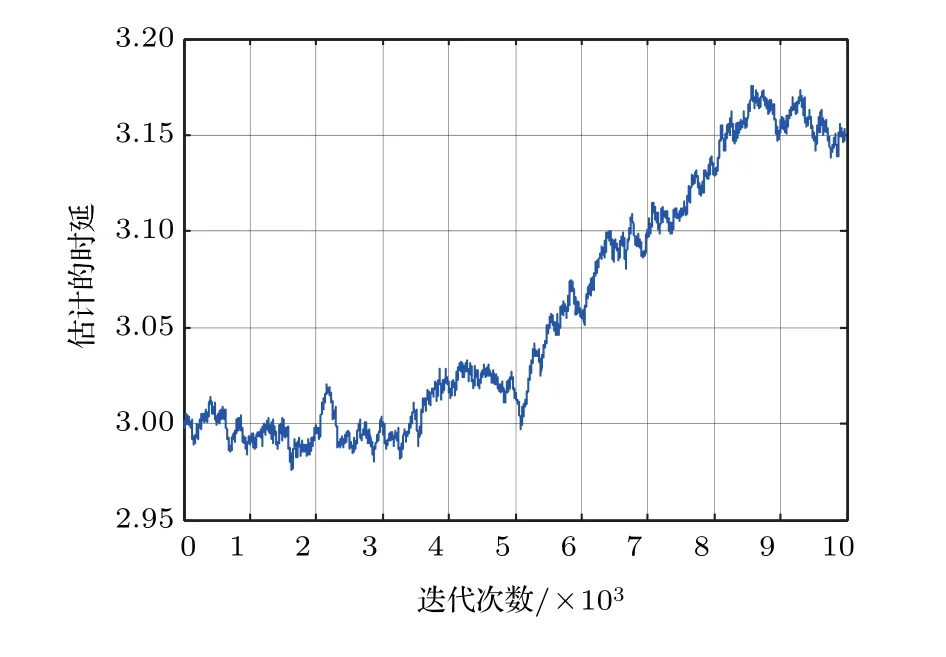
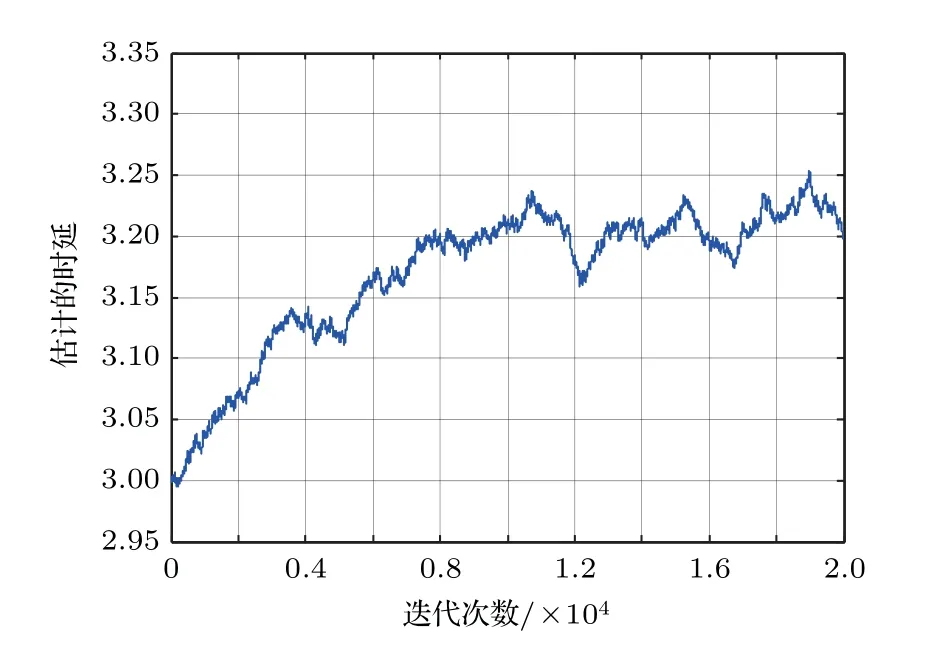
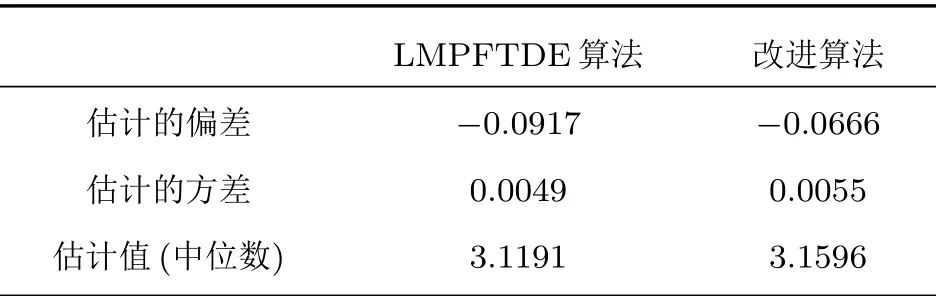
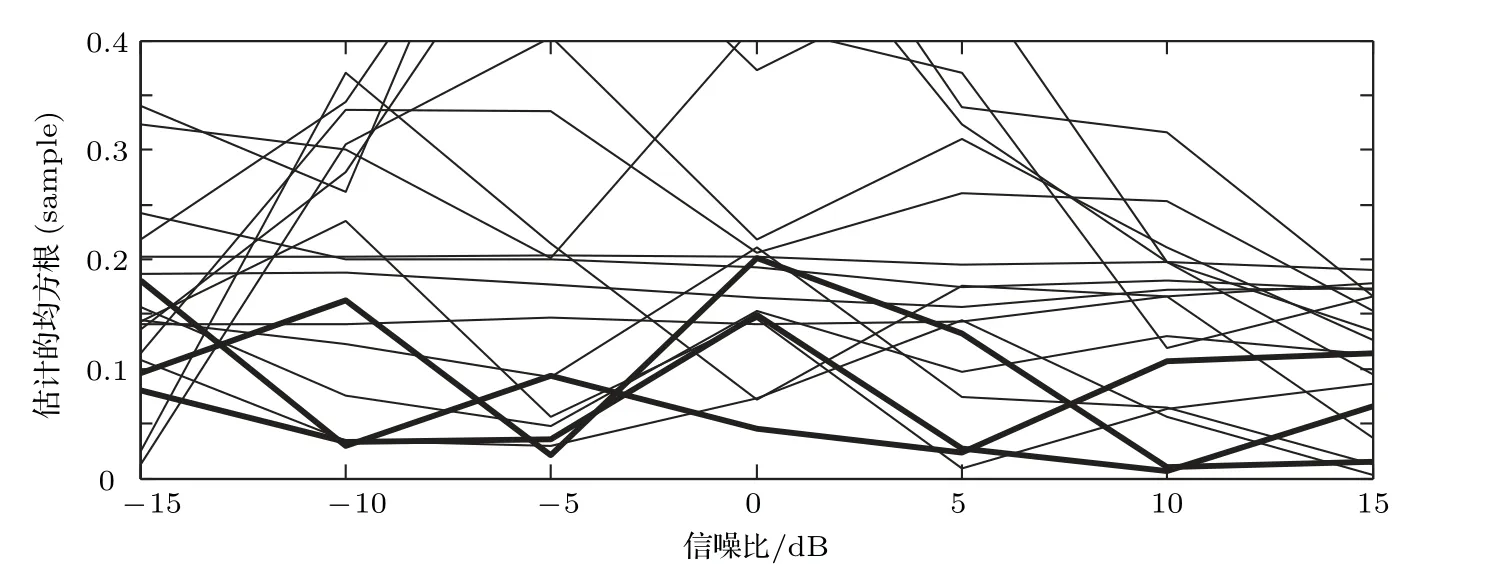
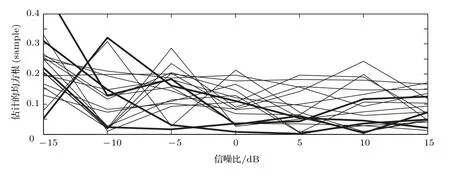
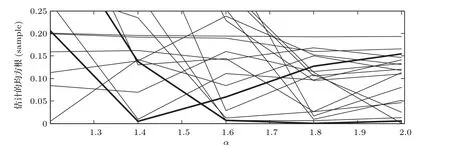
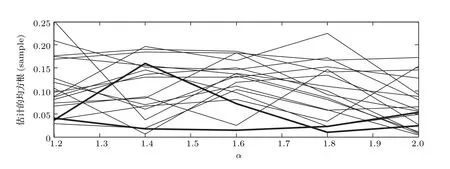
虽然代价函数E{|e(n)|p}中包含sinc 函数,它是多峰的,但是可以通过限制初始值的取值范围D −1<ˆD(0) 本文首先对两个接收信号x1(n)、x2(n)求互共变序列Rc21,接收信号x2(n)的自共变序列Rc11,削弱不相关噪声,保留原始接收信号x1(n)、x2(n)之间的时延信息,提高信噪比,抑制脉冲噪声,信号长度增加一倍,可以进行更多次迭代,更多的迭代值参考可以使时延估计值更接近真实值。接着将Rc21、Rc11当作等效的时间序列作为LMPFTDE 算法的输入信号,LMPFTDE算法的代价函数为多峰函数,直接进行迭代算法可能不收敛,迭代值在D−0.5与D+0.5之间(D为时延真值),代价函数是单峰的,所以用相关法时延估计对Rc11、Rc21先进行时延估计值整数位估计,将得到的估计值,作为LMPFTDE算法时延值迭代的初值。最后进行自适应时延估计,求出更高分辨率的时延估计值。改进的非整数自适应时延估计算法的原理框图如图1所示。 图1 改进的非整数自适应时延估计算法Fig.1 Improved fractional adaptive time delay estimation algorithm 下面通过计算机仿真实验,将本文改进的非整数自适应时延估计算法与LMPFTDE 算法的估计性能进行比较。根据信号和噪声模型构造两路接收信号,其中带限平坦谱的源S(n) 由高斯白噪声通过带宽为0.2 的6 阶巴特沃兹低通滤波器产生,脉冲性噪声由服从α稳定分布的信号来模拟,混合信噪比MSNR= 10 lg(σ2S/γv)[13]设定,其中σ2S表示源信号的方差;γv表示噪声的分散系数,取信号的长度n=10000,延迟信号s(n −D)由的61阶FIR滤波器产生,设时延真值D=3.2TS,迭代初值为3TS。共变序列的长度为20000 点,以下结果均为50 次独立实验的平均。 实验1 在相同α值和MSNR 条件下,p= 1.1,α=1.5,MSNR=0 dB,LMPFTDE算法和改进算法迭代步长µg、µD均为0.09。观察LMPFTDE 算法和改进算法收敛曲线,如图2、图3所示。 LMPFTDE 算法和改进后的时延估计算法,输入信号的长度表示算法能够进行迭代的次数。LMPFTDE 算法的输入信号长度为10000,能进行的最多迭代次数为10000;改进算法输入信号为20000,能进行的最多迭代次数为20000。 从图2、图3和表1可得出,两种算法在收敛到10000 点时,LMPFTDE 算法能够收敛到接近真值,改进算法能够收敛到真值附近,且此后在真值附近波动。用收敛过程迭代时延值的中位数作为时延估计值,改进算法迭代值的中位数更接近时延真值,改进算法的均方根误差小于LMPFTDE算法。 图2 LMPFTDE 算法收敛曲线Fig.2 Convergence curve of LMPFTDE algorithm 图3 改进算法收敛曲线Fig.3 Convergence curve of the improved algorithm 表1 LMPFTDE 算法和改进算法的估计性能比较Table1 Performance comparison on LMPFTDE algorithm and the improved algorithm 实验2 相同α值、不同MSNR 条件下,比较LMPFTDE 算法和改进算法的估计精度。取α= 1.5,MSNR 以5 dB 的间隔从−15 dB 变化到15 dB,两种算法估计值的均方根误差如图4、图5所示。 实验条件:p= 1.1,时延收敛因子与信噪比迭代步长为相等的参数,其参数以0.02 的间隔从0.01变化到0.35 的18组参数,每组参数得到的结果用一条折线表示。 图4与图5分别是以18 组参数的LMPFTDE算法和改进算法仿真的均方根误差结果,粗实线表示某一参数下算法估计较好的结果。单条折线中,改进算法在−5 dB 到8 dB 的最低均方误差均低于LMPFTDE 算法的最低均方误差,改进算法的时延收敛因子与信噪比迭代步长为0.19。在不同信噪比下,改进算法的最低均方根误差均要低于LMPFTDE 算法,但其不在一条折线上。表明参数的选择对算法性能有很大影响,在不同环境下选用合适的参数,能够获得更好的估计效果。 实验3 相同MSNR、不同α值条件下,比较LMPFTDE 算法和改进算法的估计精度。取MSNR=0 dB,α以0.2的间隔从1.2变化到2,两种算法估计值的均方根误差如图6、图7所示。 实验条件:p= 1.1,时延收敛因子与信噪比迭代步长为相等的参数,其参数以0.02 的间隔从0.01变化到0.35的18组参数。 图6与图7分别是以18 组参数的LMPFTDE算法和改进算法仿真的均方根误差结果,粗实线表示某一参数下算法估计的较好的结果。α在1.6 到2区间,LMPFTDE算法估计的最低均方根误差小于改进算法的最低均方根误差,且LMPFTDE算法最低均方误差在一条折线上,其时延收敛因子与信噪比迭代步长为0.19。在整个区间上,改进算法的较低均方根误差在同一条折线上,曲线平稳,其时延收敛因子与信噪比迭代步长为0.29;在α= 1.2 到1.6中,LMPFTDE 算法估计误差较改进算法较大。表明可以选取对应参数,使其在不同脉冲强度下均有较好的估计性能。 图4 LMPFTDE 算法的估计精度(α=1.5)Fig.4 Estimation accuracy of LMPFTDE algorithm(α=1.5) 图5 改进算法的估计精度(α=1.5)Fig.5 Estimation accuracy of the improved algorithm (α=1.5) 图6 LMPFTDE 算法的估计精度(MSNR=0 dB)Fig.6 Estimation accuracy of LMPFTDE algorithm(MSNR=0 dB) 图7 改进算法的估计精度(MSNR=0 dB)Fig.7 Estimation accuracy of the improved algorithm (MSNR=0 dB) 共变相关算法适用于处理低信噪比信号,对含脉冲噪声有好的抑制作用,能够对时延值的整数位进行准确的估计;用共变对原始信号进行处理并作为LMPFTDE算法的输入信号,输入信号长度增加一倍,可以进行更多次迭代,使时延估计值更接近真实值,消除不相关噪声,提高信噪比,保留原始序列的相位信息;将共变相关算法得到的时延估计值作为LMPFTDE算法迭代初值,最后求得非整数时延估计值。非整数自适应时延估计算法原理上也是一种互相关算法,对宽带信号的处理性能要好于窄带。 实验1 对比了两种算法的收敛过程及估计结果,分析改进算法的优势。实验2 模拟不同信噪比,对两种算法进行仿真实验,结果表明改进算法估计精度好于LMPFTDE算法,并给出改进算法的参数。实验3模拟不同脉冲环境噪声,对比LMPFTDE算法与改进算法估计的均方根误差,得到改进算法在整个区间都有好的估计效果的一组参数。 LMPFTDE 算法将迭代的初始值限定在一定范围,在这一个范围内,时延估计值是单峰函数,可以通过变步长方法使自适应收敛过程的稳态波动更小和具有较快的收敛速度,并且不需要考虑收敛到局部最优解。2.4 改进的非整数自适应时延估计算法
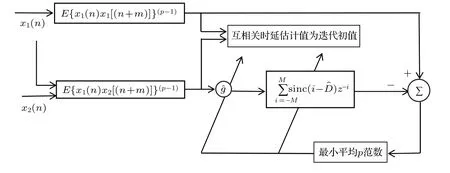
3 计算机仿真实验
4 结论

