ON A MULTI-DELAY LOTKA-VOLTERRA PREDATOR-PREY MODEL WITH FEEDBACK CONTROLS AND PREY DIFFUSION∗
Changyou WANG(王长有)Nan LI(李楠) Yuqian ZHOU(周钰谦)
1.College of Applied Mathematics,Chengdu University of Information Technology,Chengdu 610225,China
2.Department of Applied Mathematics,Southwestern University of Finance and Economics,Chengdu 610074,China E-mail:wangchangyou417@163.com;2972028881@qq.com;cs97zyq@cuit.edu.cn
Xingcheng PU(蒲兴成)Rui LI(李锐)
College of Automation,Chongqing University of Posts and Telecommunications,Chongqing 400065,China E-mail:puxc@cqupt.edu.cn;liruimath@qq.com
Abstract This article is focusing on a class of multi-delay predator-prey model with feedback controls and prey di ff usion.By developing some new analysis methods and using the theory of di ff erential inequalities as well as constructing a suitable Lyapunov function,we establish a set of easily veri fiable sufficient conditions which guarantee the permanence of the system and the globally attractivity of positive solution for the predator-prey system.Furthermore,some conditions for the existence,uniqueness and stability of positive periodic solution for the corresponding periodic system are obtained by using the fixed point theory and some new analysis techniques.In additional,some numerical solutions of the equations describing the system are given to verify the obtained criteria are new,general,and easily veri fiable.Finally,we still solve numerically the corresponding stochastic predator-prey models with multiplicative noise sources,and obtain some new interesting dynamical behaviors of the system.
Key words predator-prey model;delay;di ff usion;permanence;attractivity;periodic solution
1 Introduction
From a biological point of view,it is very important to obtain some conditions which ensures all species in multispecies community are permanent,attractive and stability.The Lotka-Volterra predator-prey model is one of the important models describing interactions among species.As we well know,species can di ff use between multiple patches.The prey species growing in weak environment often spread to advantageous environment in order to better survival and breeding of the species.So,the Lotka-Volterra model with the di ff usion can more accurately describe the interrelationships among species(see[1–3]).Song and Chen in[4]studied a two-species predator-prey system in which prey species can di ff use between two patches,and obtained some sufficient conditions which guarantee the permanence of the system and the globally attractivity of positive solution for the predator-prey system.In 2010,Wei et al.in[5]considered the periodic solution and global stability of a nonautonomous competitive Lotka-Volterra di ff usion system by using the Brouwer fixed point theorem and constructing a suitable Liapunov function.In general,in the real world,the growth rate of a natural species will not often respond immediately to changes in its own population or that of an interacting species,but will rather do so after a time lag[6].Therefore,the delay was introduced into model foundation,which will have more resemblance to the real ecosystem.There was a lot of literature related to the study of Lotka-Volterra-type population mutualism dynamical systems with delays.In[7],the authors considered a three-species Lotka-Volterra type competitivemutualism systems with discrete time delays,and some sufficient conditions on the permanence of species and the global attractivity of the system are established.Moreover,some researchers were focused on the combined e ff ects of dispersion and time-delays.In 2004,Xu et al.[8]studied a Lotka-Volterra predator-prey model with dispersion and time-delays,obtained some sufficient conditions for the existence,uniqueness and global stability of positive periodic solutions of the system by using Gaines and Mawhin!s continuation theorem of coincidence degree theory and constructing a suitable Lyapunov functional.In[9],Zhou,Shi and Song considered a nonautonomous predator-prey model with nonlinear di ff usion and time-delays.It is proved that the system is uniformly persistent under appropriate conditions,and some sufficient conditions are given for the global stability of the system by constructing a suitable Lyapunov functional.More work on di ff usion and time-delays can be found in(cf.[10–12]and the references cited therein).
On the other hand,it is very interesting in the control of ecology balance that people may wish to change the conditions of the system stability but to keep its stability still in some situation.One of the methods for the realization of it is to alter the system structurally by introducing some feedback control variables.The realization of the feedback control mechanism might be implemented by harvesting procedure or by means of some biological control scheme.In fact,in recent decade,the dynamical behavior of species for the various Lotka-Volterra systems with feedback controls have been studied in much literature,for example,see[13–16]and the references cited therein.Many interesting and important research methods and results were obtained.In 2003,Gopalsamy et al.[13]studied a two species competition system with feedback controls.And they obtained some conditions for the existence of a globally attracting positive equilibrium of the system.In[16],Chen et al.proposed a two species Lotka-volterra predator-prey system with feedback controls.By constructing two suitable Lyapunov functions,sufficient conditions which guarantee the global attractivity of the positive equilibrium are obtained,which show that enough large feedback controls could lead to the extinction of the predator species.Moreover,in recent years,attention was given to some ecosystem models with both feedback control and time delay or di ff usion(see[17–20]).In order to show that whether the feedback control variables play an essential role on the persistent property of Lotka-Volterra cooperative systems or not,Xu and Chen in[19]studied the system with time delay and feedback control,obtained some new sufficient conditions which ensure the system to be permanent,and showed that feedback control variables have no in fluence on the permanence of the system.To study the in fluence of the patch di ff usion and feedback control on existence of periodic solution,Xie and Weng in[20]considered a predator-prey model with patch-di ff usion and feedback control,and proved that the model has at least one positive periodic solution by developing some new analysis methods.
Commonly,an ecological system such as that represented by the deterministic Lotka-Volterra model is not suitable to describe the real behavior of the population dynamics.What we claim as “eedback control variables” which is mentioned above,is strictly connected to the environmental noise e ff ect.It is necessary to include the e ff ect of the environmental variables that can be deterministic,such as the variation of the temperature due to atmospheric conditions,and stochastic,due to the stochastic varaiability of all the other variables,such as growth rate,resources etc(cf.[21–28]).Moreover,the study of nonlinear dynamical systems in the presence of external noise has led to the discovery of a number of counterintuitive phenomena,with a constructive role of the noise and high fundamental and practical interests in many scienti fic areas.The presence of a noise source can change the stabiltiy of the ecological system[29].In recent years many theoretical investigations were done on noise-induced e ff ects in population dynamics[30–35].Finally,the noise source can be non-Caussian and this further enriches the dynamics[36–40].
More related works on feedback controls and time delay can be found in[41–50].However,to the best of the authors’knowledge,to this day,still less scholars consider the general nonautonomous Lotka-Volterra predator-prey system with time-delays,prey di ff usion and feedback controls.Motivated by the above works,in this paper,we propose and investigate the following two species Lotka-Volterra multi-delay predator-prey system with feedback controls and prey patch-di ff usion
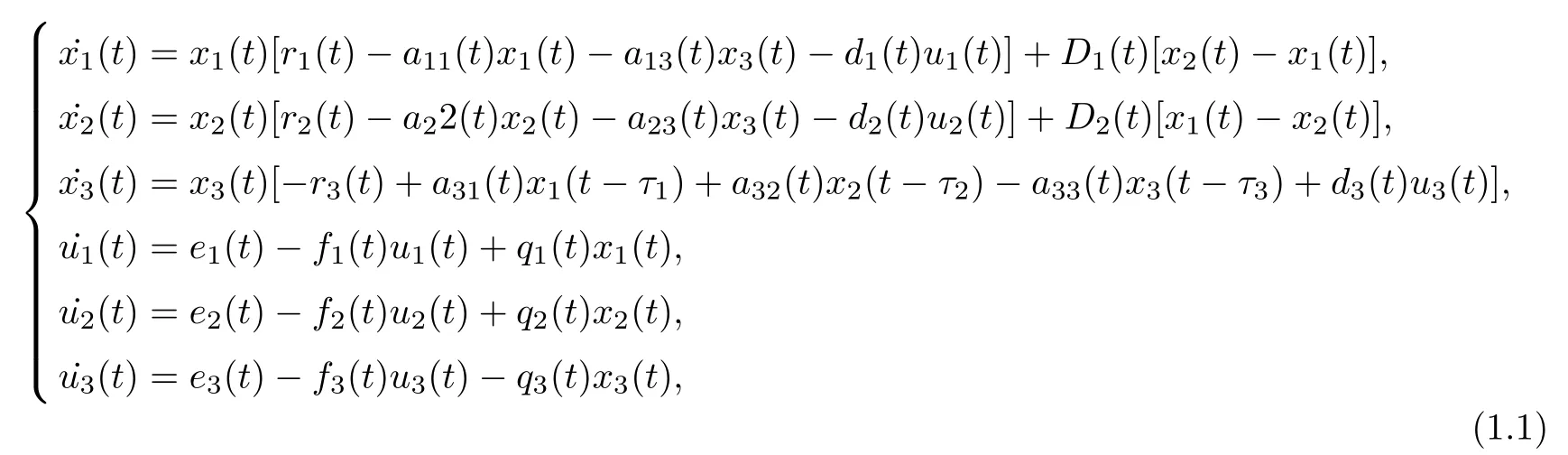
where x1(t)and x2(t)denote the density of prey species in patch 1 and patch 2,respectively,x3(t)is the density of predator species,while the prey can di ff use between two patches;ri(t)(i=1,2)denote the intrinsic growth rate of the prey species at patch 1 and patch 2,r3(t)is the death rate of the predator;aii(t)(i=1,2,3)denote the restriction density of the prey species at patch 1 and patch 2 as well as the predator species,respectively.a13(t)and a23(t)are the capturing rate of the predator,a31(t)and a32(t)are the conversion rate of nutrients of the predator;Di(t)are the dispersion rate of prey species at patch i,(i=1,2),ui(t)(i=1,2,3)are the feedback control terms.Furthermore,in view of the biological signi ficance of the above parameters,we assume that ri(t),aii(t),di(t),ei(t),fi(t),qi(t)(i=1,2,3),a13(t),a23(t),a31(t),a32(t),D1(t)and D2(t)are continuous,bounded and strictly positive functions on[0,+∞), τ1,τ2,τ3are positive constants representing delays.
Due to biological interpretation of system(1.1),it is reasonable to consider only positive solution of(1.1),in other words,to take admissible initial conditions
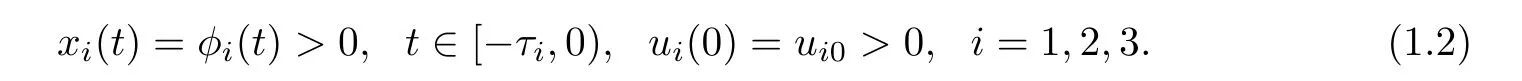
Obviously,the solutions of system(1.1)with the initial values(1.2)are positive for all t≥0.
This paper is organized as follows:in Section 2,we provide the conditions for the permanence to system(1.1).In Section 3,by constructing a nonnegative Lyapunov function,we shall derive sufficient conditions for the globally attractive of positive solution for system(1.1).In Section 4,some conditions for the existence,uniqueness and stability of a positive periodic solution for the corresponding periodic system are obtained by using the fixed point theory and some new analysis method.Some numerical solutions of the equations describing the system are given in Section 5 to verify the obtained criteria are veri fiable.
2 Permanance
In order to establish a permanence result for system(1.1),we introduce firstly the following notations and de finitions.Given a continuous and bounded function g(x)de fined on[0,+∞),we set
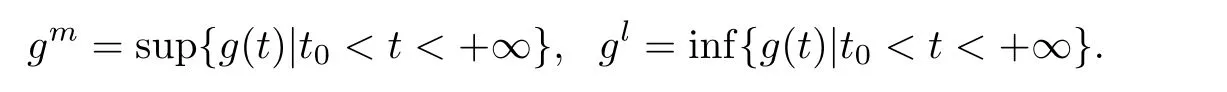
De finition 2.1System(1.1)is called permanent,if there exist positive constants Mi,mi(i=1,2),Ni,ni(i=1,2,3)and T,such that
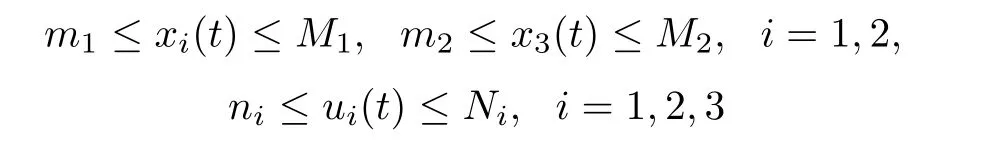
for any positive solution Z(t)=(x1(t),x2(t),x3(t),u1(t),u2(t),u3(t))of system(1.1)as t>T.
As a direct corollary of Lemma 2.1 of Chen[51],we have
Lemma 2.2If a>0,b>0 andwhen t≥0 and x(0)>0,then we have
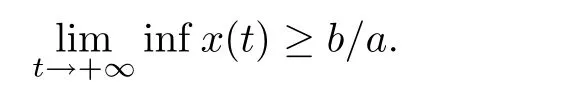
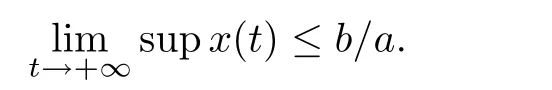
As a direct corollary of Lemma 2.2 of Chen[51],we have
Lemma 2.3If a>0,b>0 andwhen t≥0 and x(0)>0,then we have

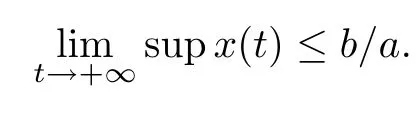
Lemma 2.4(see[52],Lemma 2.2) Assume that for y(t)>0,it holds that
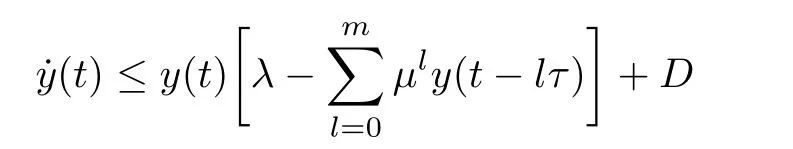
with initial conditions y(t)= φ(t)≥ 0 for t∈ [−mτ,0)and φ(0)>0,where

are constants,then there exist a positive constant My<+∞such that

where y=y∗is the unique solution of the equation y(λ−µy)+D=0.
Lemma 2.5(see[52],Lemma 2.3) Assume that for y(t)>0,it holds that



For system(1.1),we let


Theorem 2.6Assume that system(1.1)satis fies the following conditions
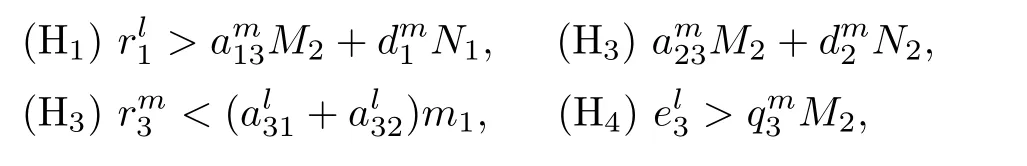
then system(1.1)is permanent.
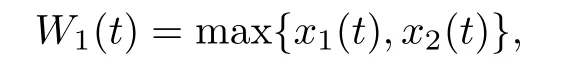
ProofAccording to the first and the second equations of system(1.1),we de fine and calculate the upper right derivative of W1(t)along the positive solution of system(1.1),then we have that
(P1)If x1(t)≥x2(t),then
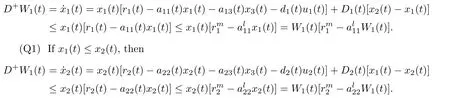
From(P1)and(Q1),we have
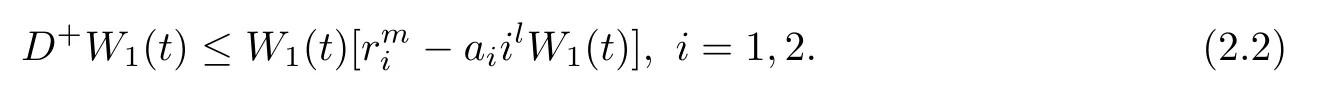
By(2.2)we can derive
(A1)If W1(0)=max{x1(0),x2(0)}≤M1,then max{x1(t),x2(t)}≤M1,t≥0.
(B1)If W1(0)=max{x1(0),x2(0)}>M1,take appropriate α>0,we have the following three cases
(a1)W1(0)=x1(0)>M1,(x1(0)>x2(0));
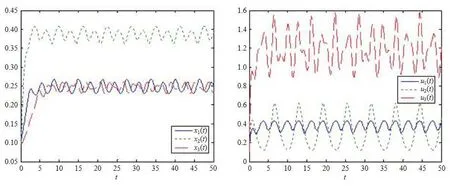
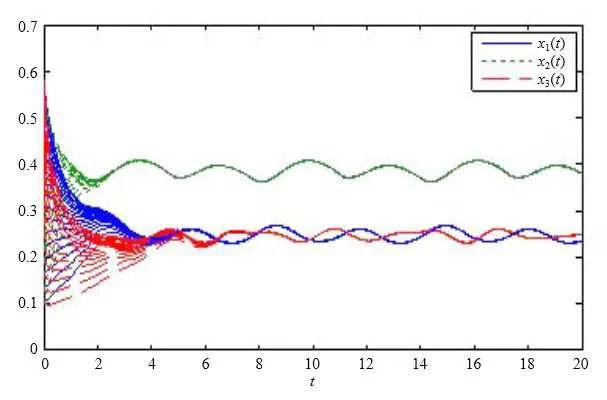
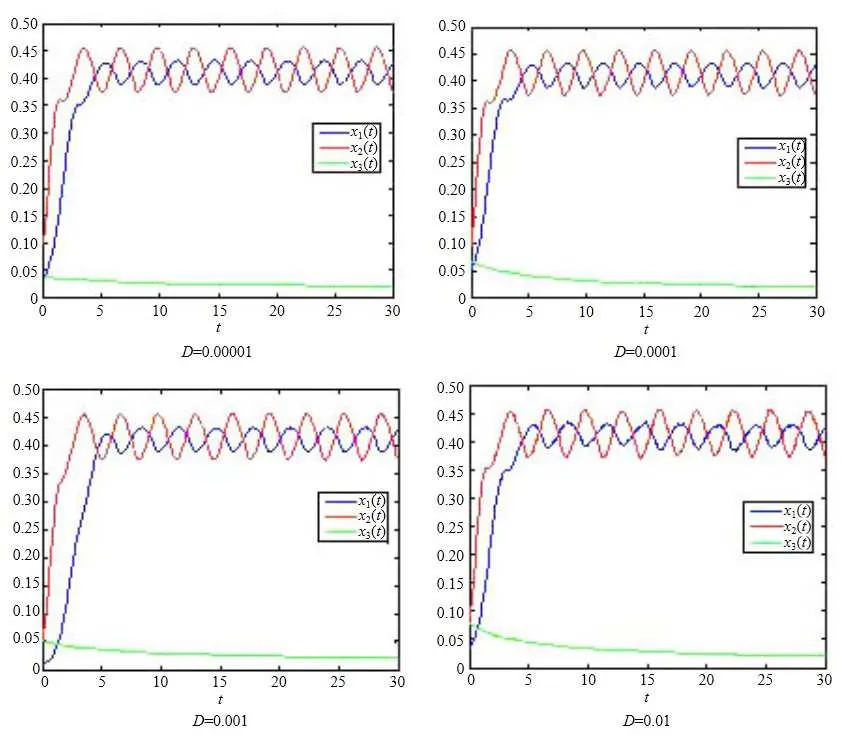
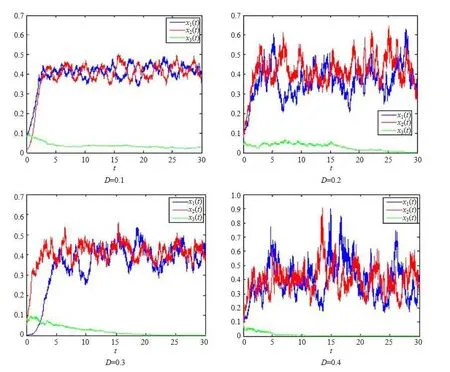
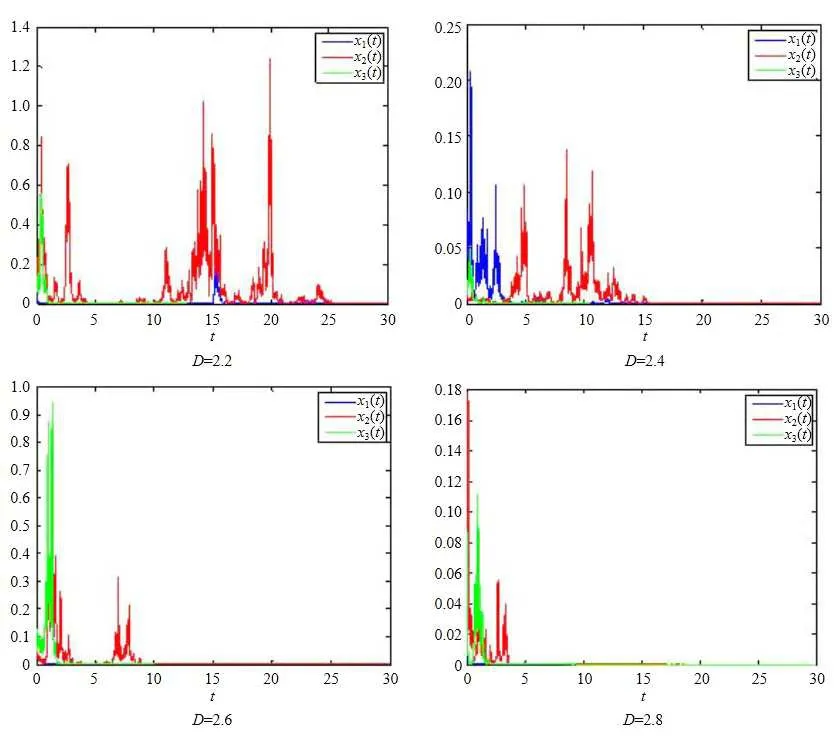
(b1)W1(0)=x2(0)>M1,(x1(0) (c1)W1(0)=x1(0)=x2(0)>M1.Further,we have If(a1)holds,then there exists ε>0 such that W1(t)=x1(t)>M1,t∈ [0,ε).Moreover,it holds that If(b1)holds,then there exists ε>0 such that W1(t)=x2(t)>M1,t∈ [0,ε).Thus,we have that If(c1)holds,similar to(a1)and(b1),we have From what we discuss above,we can conclude that if W1(0)>M1,then W1(t)is strictly monotone decreasing with speed at least α.So there exists T1>0 such that if t ≥ T1,then W1(t)=max{x1(t),x2(t)}≤M1.Moreover,we have and According to the sixth equation of system(1.1),one has that And by Lemma 2.2,we have By the third equation of system(1.1),we have that And from the Lemma 2.4,we derive that For the fourth and the fifth of system(1.1),we have and By Lemma 2.2,we can get and On the other hand,according to the first and the second equations of system(1.1),we de fine W2(t)=min{x1(t),x2(t)},then calculating the lower right derivative of W2(t)along the positive solution of system(1.1),we have (P2)If x1(t)≤x2(t),then (Q2)If x1(t)≥x2(t),then From(P2)and(Q2),it is easy to obtain By(2.9),we can obtain that (A2)If W2(0)=min{x1(0),x2(0)}≥m1,then min{x1(t),x2(t)}≥m1,t≥0. (B2)If W2(0)=min{x1(0),x2(0)} (a2)W2(0)=x1(0) (b2)W2(0)=x1(0) (c2)W2(0)=x1(0)=x2(0) If(a2)holds,then there exists ε >0 such that W2(t)=x1(t) If(b2)holds,then there exists ε>0 such that W2(t)=x2(t) If(c2)holds,in the same way,we have that From(a2),(b2)and(c2),we can get that if W2(0) and For the third equation of system(1.1),we have By Lemma 2.5,we have From the fourth and the fifth of system(1.1),we have and And by Lemma 2.2,we can get and According to the sixth equation of system(1.1),we have From Lemma 2.2,it holds that From(2.3)–(2.8)and(2.10)–(2.15),this ends the proof of Theorem 2.6. ? In this section,we will obtain the sufficient conditions for the global attractivity of system(1.1).Firstly,on the global attractivity of system(1.1),we have the following de finition and Lemma.The strategy of proof is to construct a suitable Lyapunov function. De finition 3.1System(1.1)is said to be globally attractive,if there exists a positive solution X(t)=(x1(t),x2(t),x3(t),u1(t),u2(t),u3(t))of system(1.1)such that for any other positive solution Y(t)=(y1(t),y2(t),y3(t),v1(t),v2(t),v3(t))of system(1.1). Theorem 3.3Assume that system(1.1)satis fies(H1)–(H4)and the following conditions where Then system(1.1)is globally attractive. ProofLet X(t)=(x1(t),x2(t),x3(t),u1(t),u2(t),u3(t))be a positive solution of system(1.1)and Y(t)=(y1(t),y2(t),y3(t),v1(t),v2(t),v3(t))be any positive solution of system(1.1)with initial conditions(1.2).From Theorem 2.6,we know that there exists positive constants M1,M2,m1,m2,Ni,ni,i=1,2,3 and T>0,such that if t≥T,then We de fine and calculate the upper right derivative of Vi(t),i=1,2 along the solutions of system(1.1),then we have where (1)if x1(t)>y1(t),then (2)if x1(t) (3) if x1(t)=y1(t),the same conclusion as(1)and(2)holds.Then,from the above conclusions,we obtain Similarly,it is available that From(3.1)–(3.3),we have De fine V31(t)=|lnx3(t)−lny3(t)|,and calculate the upper derivative of V31(t)along the solution of system(1.1),we obtain De fine It follows from(3.5)and(3.6),we have Now,we de fine where Then it follows from(3.7)–(3.9)that,for t≥ T+ τ, De fine V4(t)=|lnu1(t)−lnv1(t)|,V5(t)=|lnu2(t)−lnv2(t)|,V6(t)=|lnu3(t)−lnv3(t)|,and calculate the upper right derivative of V4(t),V5(t),V6(t)along the solutions of system(1.1),we have From assumption(H5),there exists a constant α >0 and T∗>T+τ such that for all t≥ T∗,we have Integrating both sides of(3.14)on interval[T∗,t]and by(3.15),we have Hence,V(t)is bounded on[T∗,+∞]and we obtain Therefore, By hypothesis(H1)–(H5)and Theorem 2.6,we can obtain that|xi(t)− yi(t)|,|ui(t)− vi(t)|,i=1,2,3 and their derivatives remain bounded on[T∗,+∞).As a consequence,|xi(t)−yi(t)|,|ui(t)−vi(t)|,i=1,2,3 are uniformly continuous on[T∗,+∞).By Lemma 3.2,we can conclude that This completes the proof of Theorem 3.3,and the solutions of system(1.1)is globally attractive. Assuming that coefficients of system(1.1)are positive continuous,ω-periodic functions,then system(1.1)is changed to periodic system.In this section,we shall obtain conditions for the existence,uniqueness and stability of a positive periodic for system(1.1)by using the fixed point theory and some new analysis method.For convenience,we give firstly the following lemma. Lemma 4.1(see[54]) Let S⊂Rnbe convex and compact.If mapping T:S→S is continuous,then there exists a fixed point.That is to say,there exists x∗∈ S such that T(x∗)=x∗. Theorem 4.2Assume that system(1.1)is a periodic system and satis fies conditions(H1)–(H5),then system(1.1)has a positive unique ω-periodic solution,which is globally asymptotically stable. ProofAccording to the existence and uniqueness theorem of solutions of functional differential equations,we can de fine a Poincare mapping T:as follow where X(t,ω,X0)=(x1(t),x2(t),x3(t),u1(t),u2(t),u3(t))be a positive solution of the system(1.1)with the initial conditions(1.2).And de fine In this section,we will give an example to illustrate the results obtained in this paper.To facilitate the validation of the Theorem 4.2 in which the system is ω-period system,so we choose the 2π-periodic function as the coefficients of system(1.1)and consider the following multi-delay periodic predator-prey model with feedback control and prey di ff usion.In view of the conditions of Theorem 4.2,we choose some particular values of parameters shown in models(5.1)–(5.2)according to the calculation.Of course,the selection of the parameters in the models is not unique.By employing the software package MATLAB 7.1,we can get some numerical solutions of the following system(5.1)with the initial conditions(5.2). where time delay τ1=0.01,τ2=0.02,τ3=0.03 and the initial conditions are as follows By calculating,we have Figure 1 The numerical solution of system(5.1)with the initial conditions(5.2) Figure 2 The numerical solution of system(5.1)with the di ff erent initial conditions Figure 3 The dynamic behavior of systems(5.1) It is easy to show that system(5.1)satis fies the conditions of Theorem 2.6,Theorem 3.3 and Theorem 4.2.From Theorem 2.6 and Theorem 3.3,we have that the system is permanent and globally attractive.By means of Theorem 4.2,system(5.1)has a positive unique periodic solution,which is globally asymptotic stability.The simulation of the whole system have been carried out by MATLB,we can get the numerical solutions of system(5.1)which are shown in Figure 1 to Figure 3.Figure 1 shows that the permanence of system(5.1)with time delay and the initial conditions(5.2).From Figure 2,it is not difficult to find that system(5.1)is globally attractive.Figure 3 shows that the dynamic behavior of system(5.1). It is well known that the environmental noise is extremely important in modeling natural phenomena such as ecosystems and population dynamics.Nowadays,the dynamics of populations can not be modeled without taking into account the interaction between the ecological system and environmental noise,always present in nature.In fact,the environmental noise acts constructively,producing counter-intuitive e ff ects and interesting noise-induced phenomena,such as stochastic resonance,noise enhanced stability and resonant activation.So,we will consider the following corresponding stochastic predator-prey models with multiplicative noise sources of form where the ξi(t)are δ-correlated Gaussian white noise sources with zero mean,that is,hδi(t)i=0 andwith Dithe noise intensities(here,we choose all equal the noise intensities,that is Di=D),time delay τ1=0.01,τ2=0.02,τ3=0.03,and the initial conditions are as follows By employing the MATLAB 7.1 software,we can obtain some numerical solutions of models(5.3)–(5.4)with di ff erent noise intensities which are shown in Figure 4 to Figure 6.From Figure 4,we can find that the new stochastic equations(5.3)–(5.4)have a almost deterministic solutions when the noise intensities is very very low.Moreover,Figure 5 shows that the predator species tend to be extinct when the noise intensities increased to 0.2.From Figure 6,it is showed that the prey and predator species all tend to be extinct when the noise intensities increased to 2.2.By comparing the results shown in Figure 4 to Figure 6 with those shown in Figure 1 to Figure 3,it is obvious that the stochastic environmental noise can a ff ects the permanence,periodic and stability of the predator-prey system. Figure 4 The numerical solutions of system(5.3)–(5.4)with very low noise intensities Figure 5 The numerical solutions of system(5.3)–(5.4)with low noise intensities Figure 6 The numerical solutions of system(5.3)–(5.4)with high noise intensities In this paper,we propose and investigate a class of two-species Lotka-Volterra multi-delay predator-prey system with feedback controls and prey patch-di ff usion.By using the comparison theorem and some new analysis methods as wall as constructing the appropriate Lyapunov function,the sufficient conditions to ensure the permanence and global stability of the system are obtained.Furthermore,some conditions for the existence,uniqueness and stability of a positive periodic solution for the corresponding periodic system are obtained by de fining a Poincare mapping and using the Brouwer fixed point theorem.In additional,some numerical solutions of the equations describing the system are given to illustrate our results.Finally,we still solve numerically the corresponding stochastic predator-prey models with multiplicative noise sources,and obtain some new interesting dynamical behaviors of the system. Time delay and di ff usion are very common phenomenon in the ecological system,but at present,some scholars are not deep enough in these areas.Added time-delay and the di ff usion term in this paper are relatively simple,and can not re flect the more general ecological system,but which is the key points of our future research,including the multi-delay extended to in finite delay and other aspects.By analyzing the system after adding the feedback control,we can find that the feedback control items have in fluence both on the permanence and global stability of the original system.Therefore,in some ecosystems,some species can be controlled to maintain the balance and sustainable development of the ecosystem,and this is also the practical signi ficance of this topic.In additional,by comparing the numerical solutions of equations(5.1)–(5.2)with those of equations(5.3)–(5.4),it is found that the stochastic environmental noise can a ff ects the permanence,periodic and stability of the periodic predator-prey system.

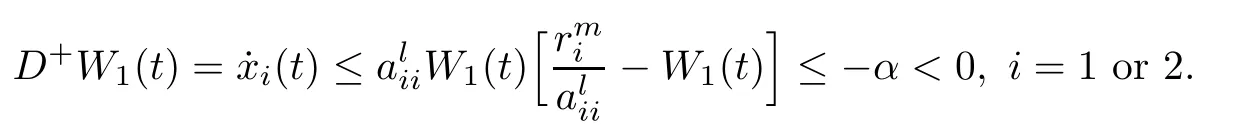
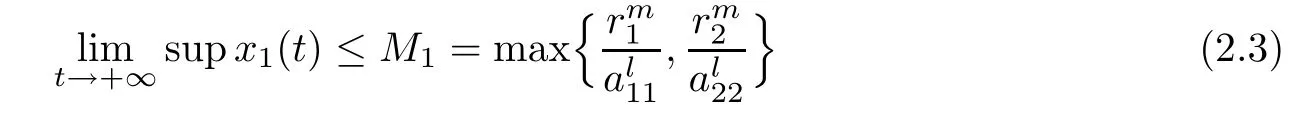

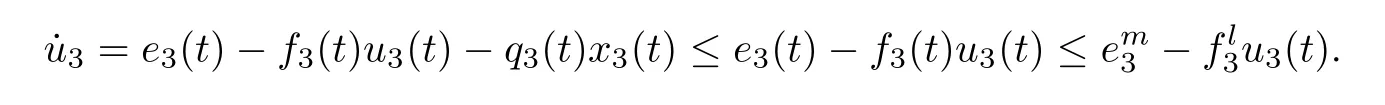
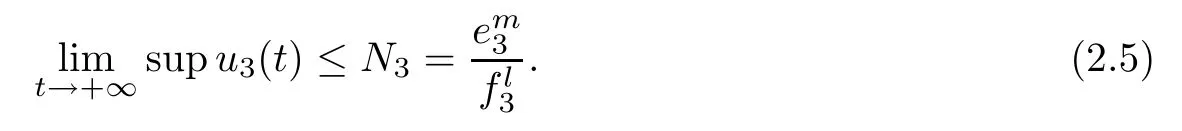
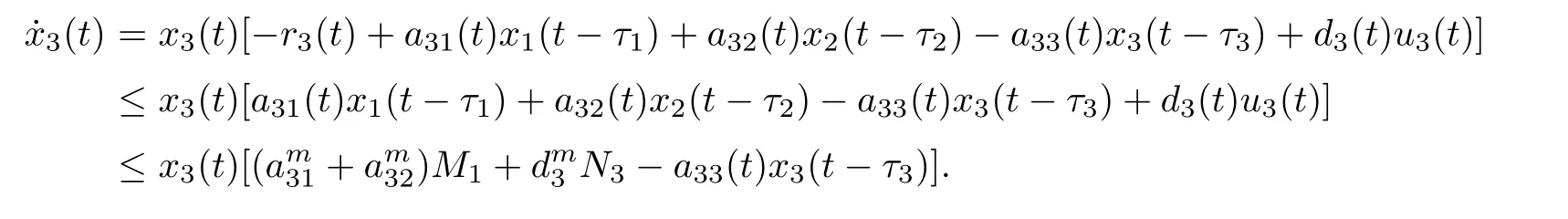
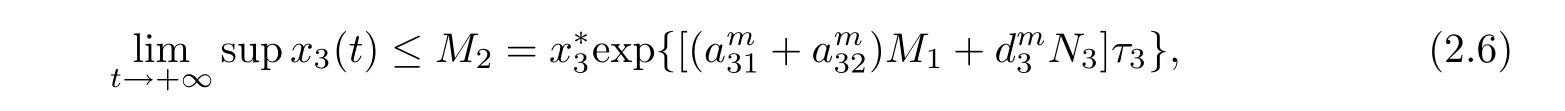
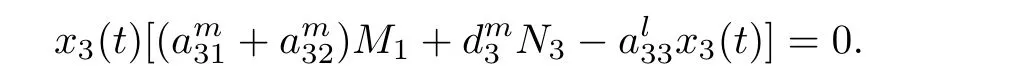

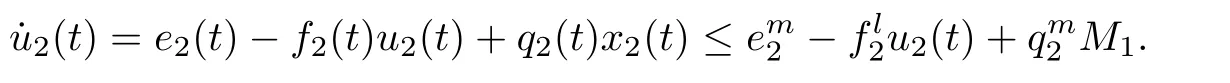
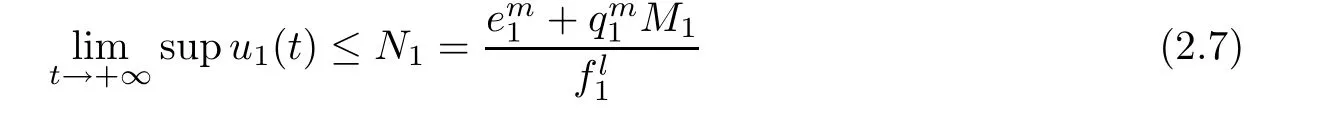
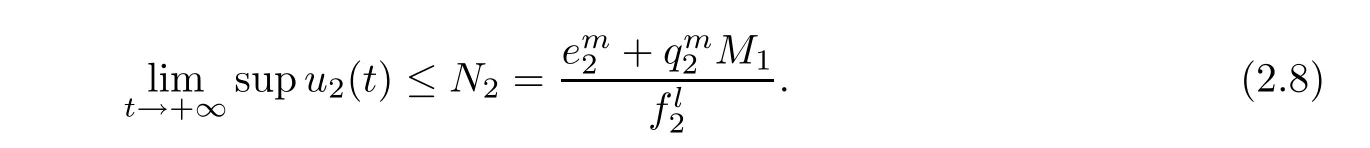
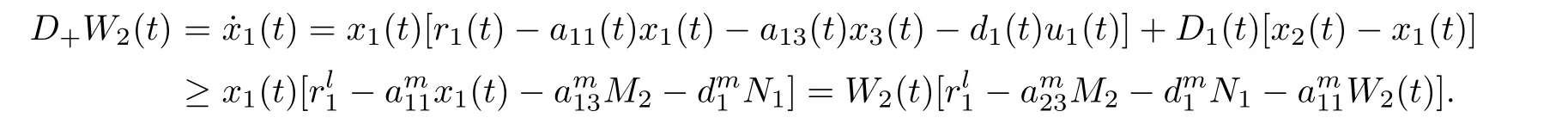
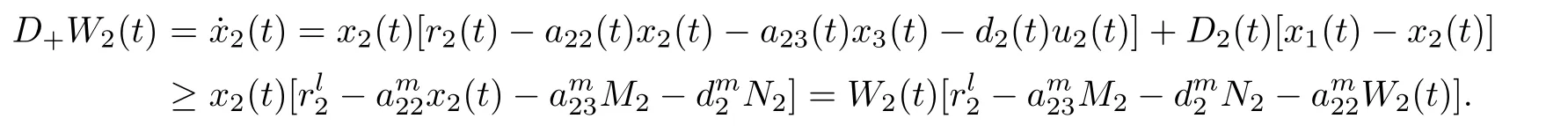
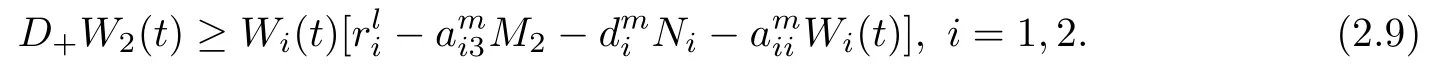
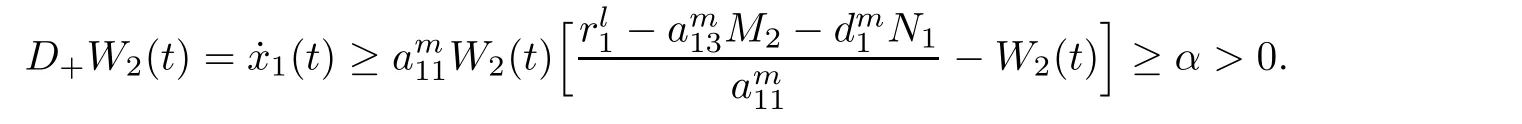
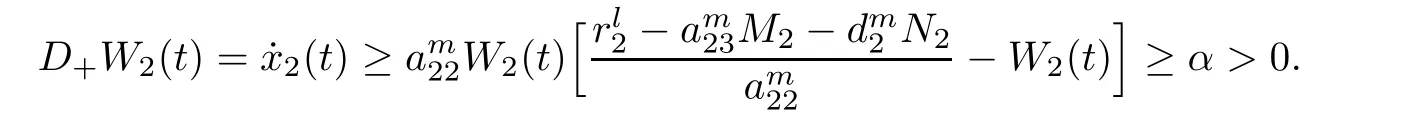
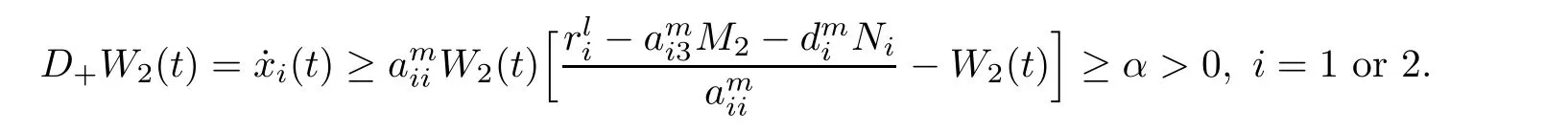

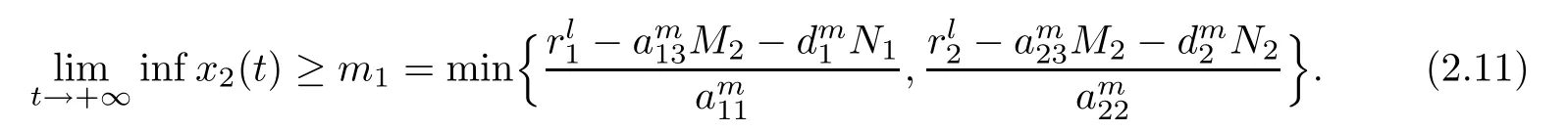
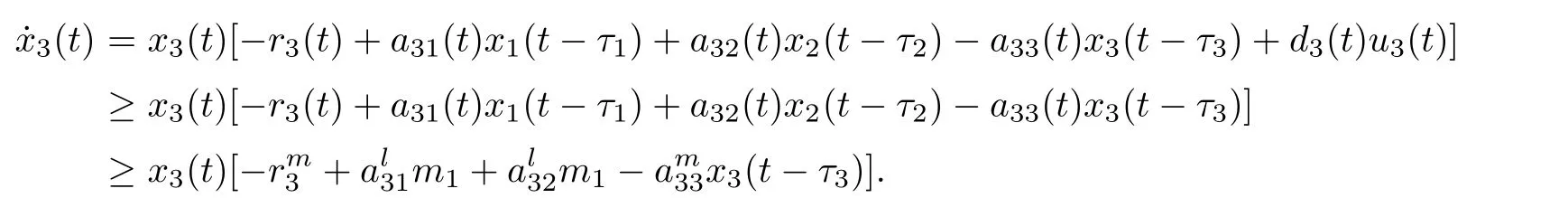
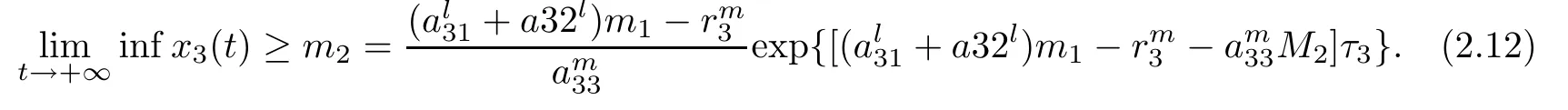
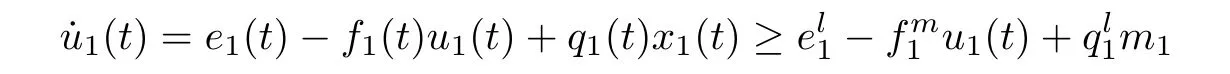
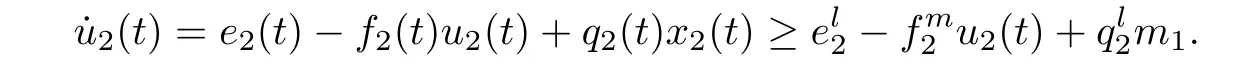

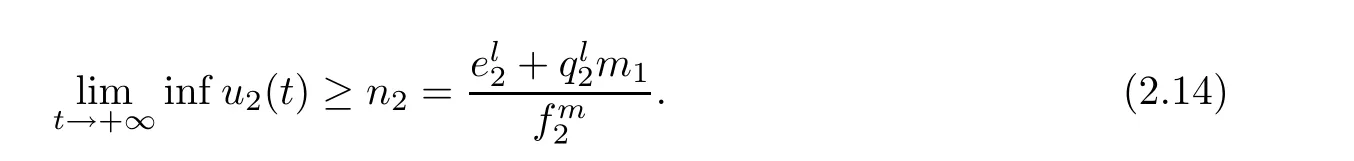
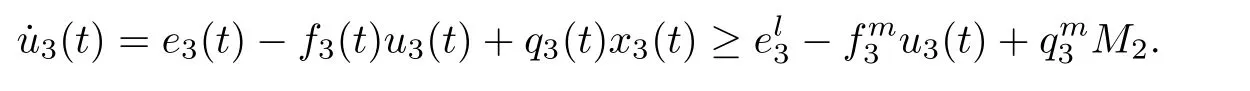
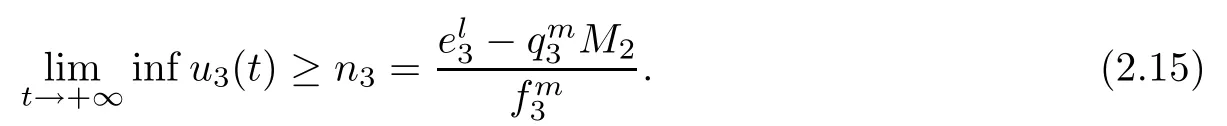
3 Globally Attractive
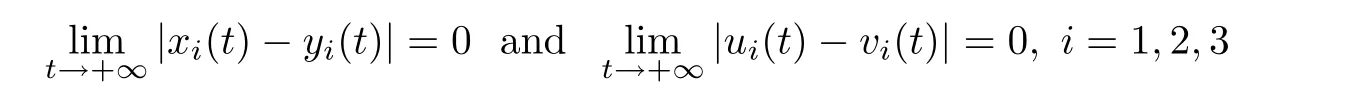

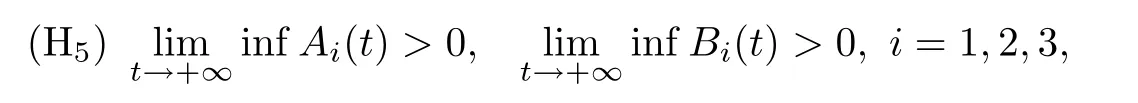

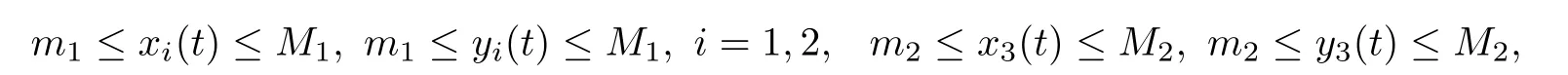
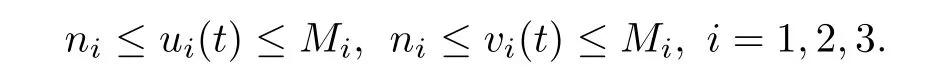

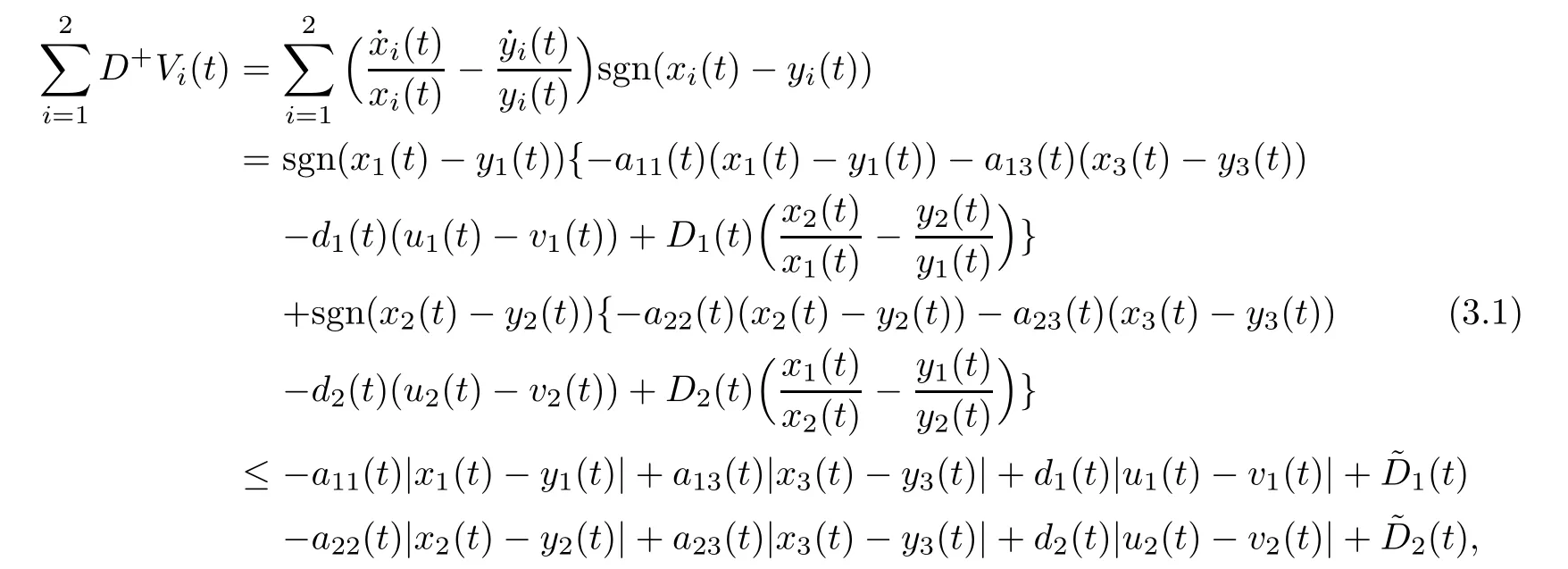
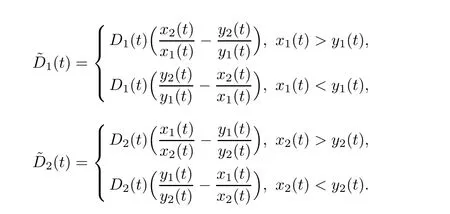




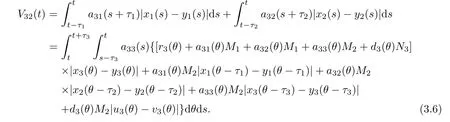

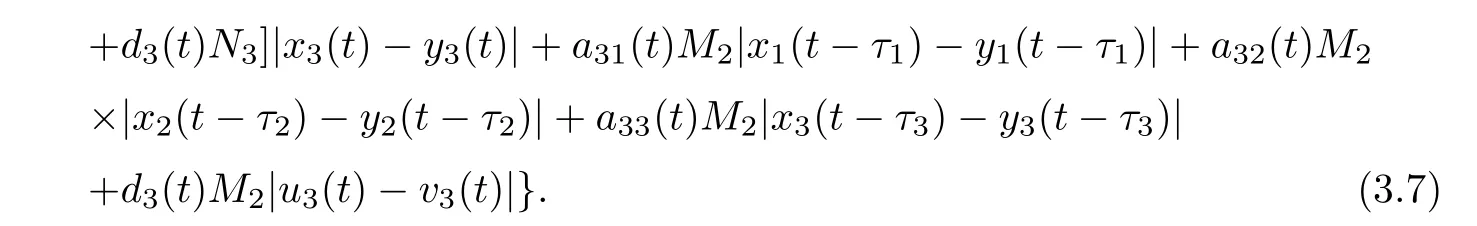
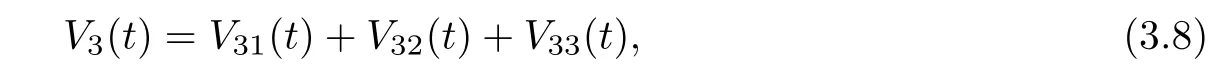
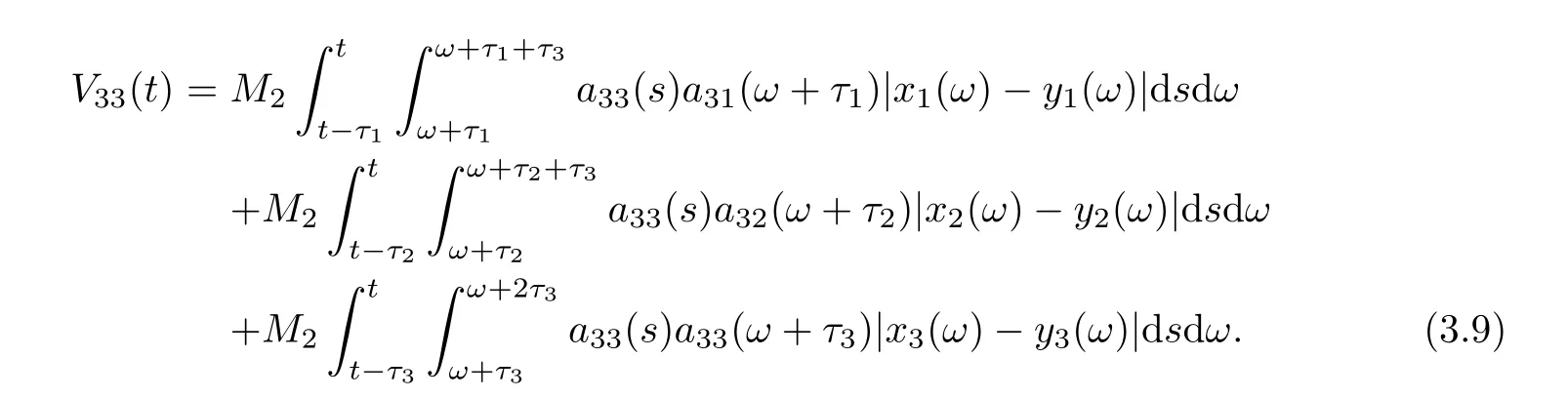

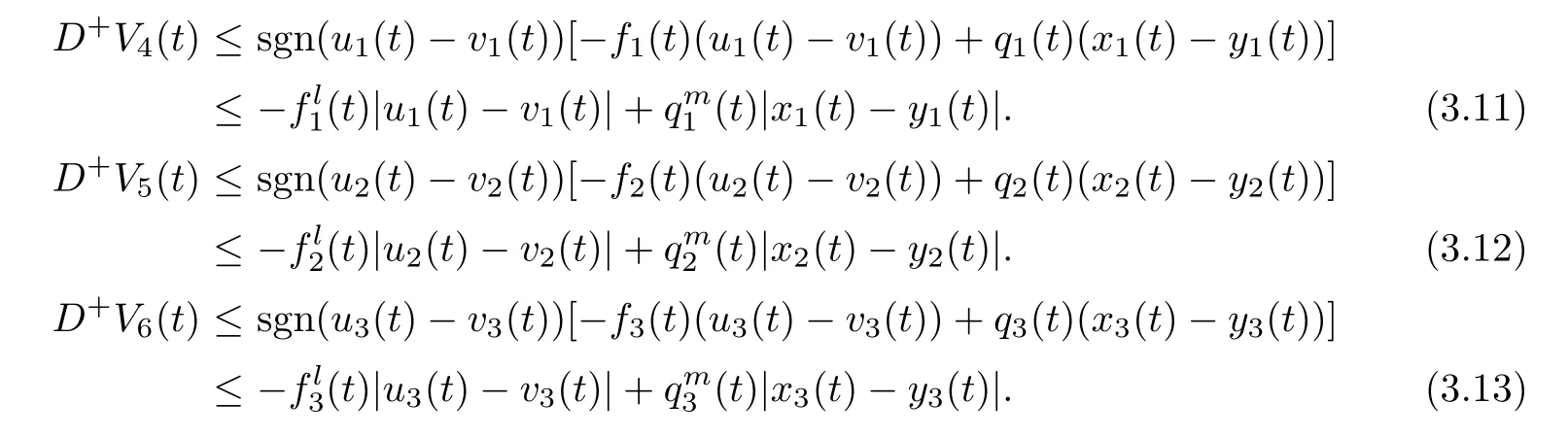
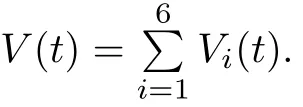
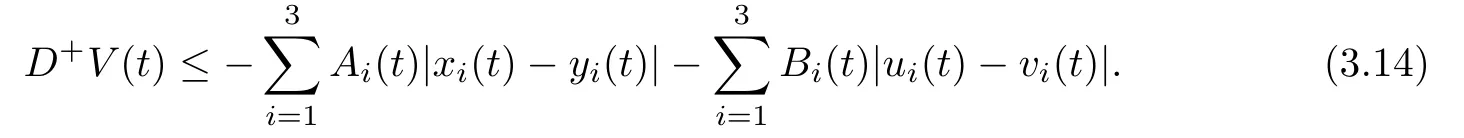

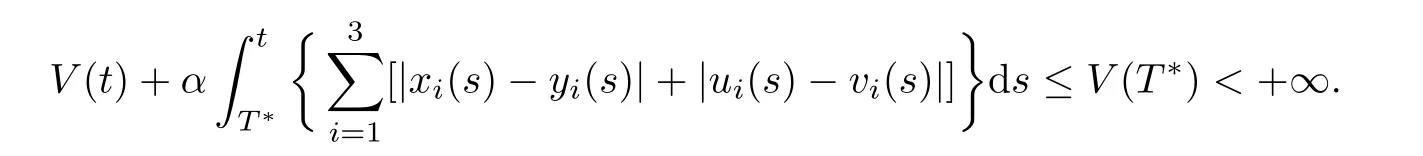
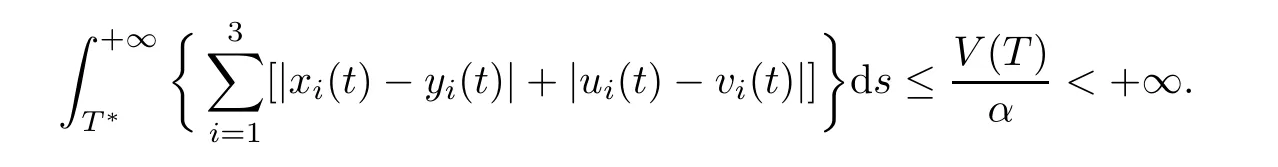
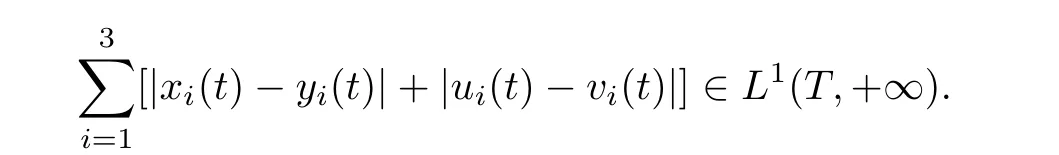
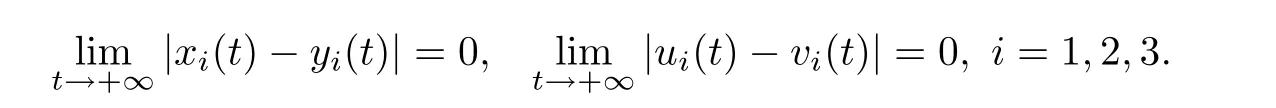
4 Periodic Solution

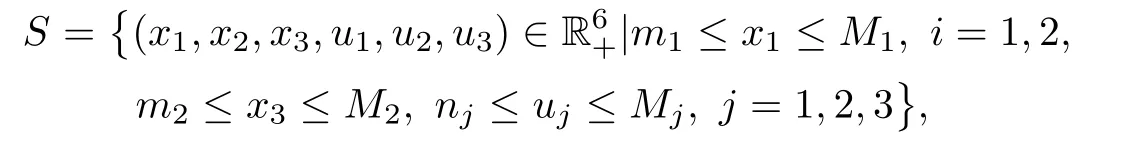
5 Numerical Simulation
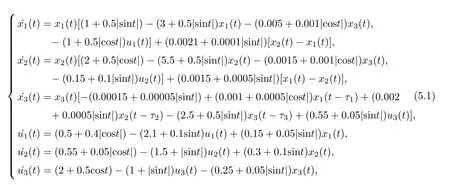
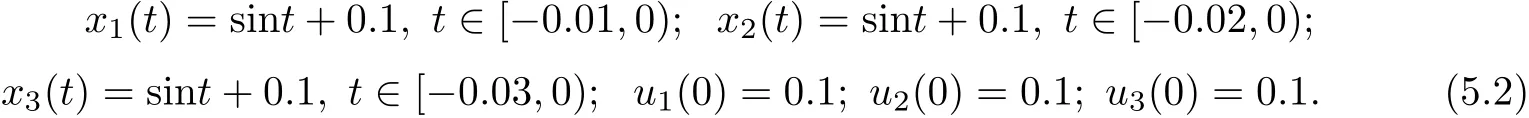
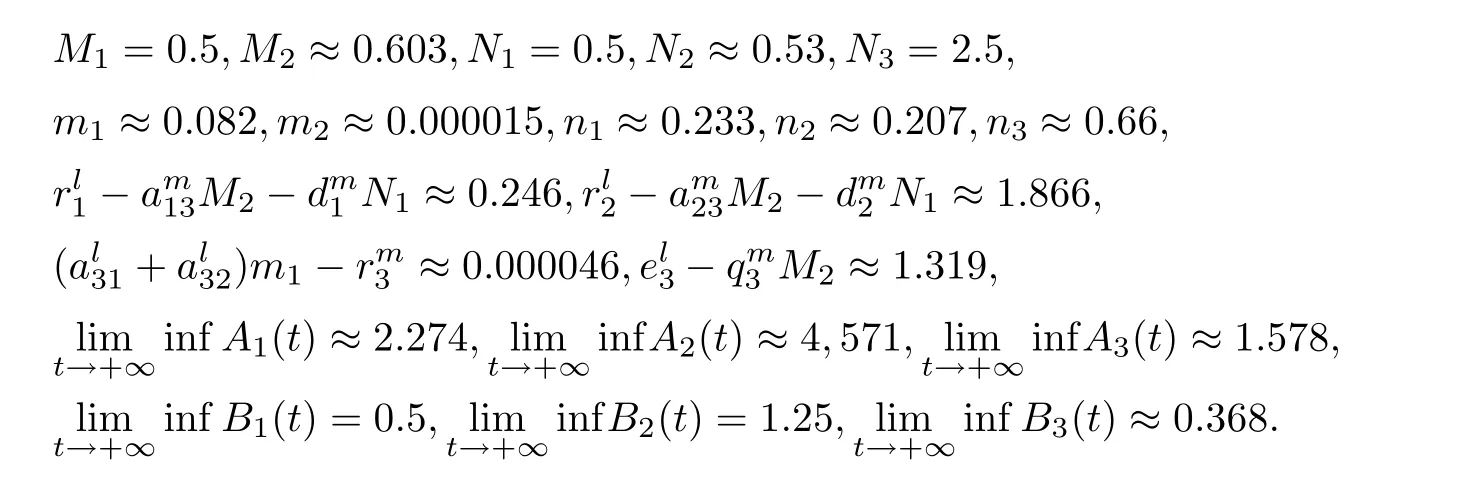

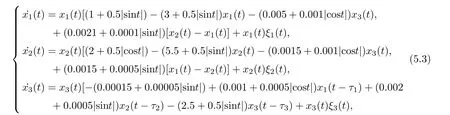
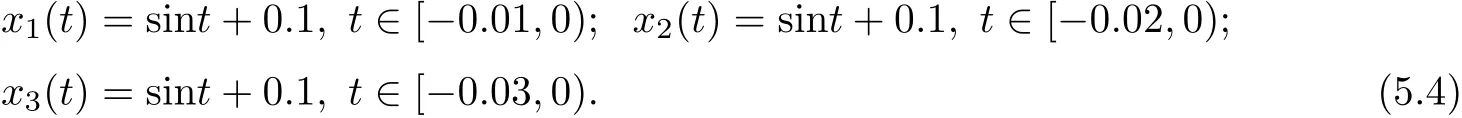
6 Conclusion
 Acta Mathematica Scientia(English Series)2019年2期
Acta Mathematica Scientia(English Series)2019年2期
