Dynamic Response Solution of Multi-Layered Pavement Structure Under FWD Load Appling the Precise Integration Algorithm

Zejun Han,Hongyuan Fang ,Juan Zhang and Fuming Wang

Abstract: The pavement layered structures are composed of surface layer,road base and multi-layered soil foundation.They can be undermined over time by repeated vehicle loads.In this study,a hybrid numerical method which can evaluate the displacement responses of pavement structures under dynamic falling weight deflectometer (FWD)loads.The proposed method consists of two parts:(a)the dynamic stiffness matrices of the points at the surface in the frequency domain which is based on the domain-transformation and dual vector form equation,and (b)interpolates the dynamic stiffness matrices by a continues rational function of frequency.The mixed variables formulation (MVF)can treat multiple degree of freedom systems with considering the coupling term between degree of freedoms.The accuracy of the developed method has been demonstrated by comparison between the proposed method and published results from the other method.Then the proposed method can be applied as a forward calculation technique to emulate the falling weight deflectometer test for multi-layered pavement structures.

Key words:Falling weight deflectometer,dynamic stiffness,mixed-variable formulation,forward calculation model,time-domain.

1 Introduction

Roads play an important role in urban infrastructure which are regarded as the lifeblood of the city.Meanwhile,the cost for their maintenance is expensive.Hence the local governments and expressway companies always make the detection and diagnostic of road system a top priority.Various detection methods have been presented to detect the pavement structures.Nowadays,the FWD test has been widely applied to measure pavement deflections as a non-destructive testing method because of high testing efficiency and applying dynamic loads with high-amplitude familiar to the acting loads by the wheels of a truck or car.The modulus,layer thickness and other material properties of the pavement can be calculated by inverse model of FWD deflection basin without destroying pavement.The accuracy of the forward calculation model which can represent the dynamic responses of the pavement structures is a major concern for inverse calculation.However,the inversion process applied to analyze the FWD testing data is mainly based on static analysis of layered pavement structures.The dynamic behaviors of the FWD loads are ignored in the static analysis method.To overcome the shortcoming,a high precise dynamic simulation model has been presented with the effect of dynamic FWD load is completely considered.And the deflection displacement histories were compared with the FWD testing data.

Over the decades,people usually used the empirical methods to evaluate pavement behavior.However,in these years,the increase in the number of vehicles added the weight on the roads.As a result,the empirical methods are no longer applicable.Various approaches have been developed to simulate the mechanical behavior in layered media under the traffic load.Kausel et al.[Kausel and Roësset (1981)] and Kausel [Kausel (1981)] gave the modified stiffness matrices of stratified soils for calculating responses to dynamic loads by the thin layer method.Magnuson [Magnuson (1988)] integrated oscillation functions by a special method to obtain a numerical result.The functions are expanded into Fourier-Bessel series.Later,Stolle [Stolle (1991)] presented a discrete layer model to analyze the static response of a pavement structure subjected to a dynamic FWD load with an explicit time marching.The displacement field is also expressed by a Fourier-Bessel series expansion.A three-dimensional infinite elements method for the dynamic response analysis in a multi-layered media underlain by a half-space was performed by Yun et al.[Yun and Kim (2006)],and an efficient integration procedure was also proposed for calculating the element matrices involving multiple wave components.Al-Khoury et al.[Al-Khoury,Kasbergen and Scarpas (2001)] and Gu et al.[Gu,Wang,Cheng et al.(2014)] developed the spectral element method for dynamic analyses of pavement structures under the FWD load pulse,respectively.Liang and Zeng [Liang and Zeng (2002)] presented an efficient solution technique for the transient wave propagation in a multi-layered soil medium due to axisymmetric dynamic loads applied at the surface.Guzina et al.[Guzina and Fata (2015)] proposed a numerical method to simulate the forced vertical vibration when an annular foundation rests on a stratified soil by the second kind Fredholm integral equation.Uddin et al.[Uddin and Garza (2010)] proposed a 3D finite-element model of pavement structure subjected to an FWD load to calculate the structural dynamic response of pavement;Kim et al.[Kim and Mun (2008)] presented a fast spectral analysis way to simulate the dynamic response of an axisymmetric layered structure imposed FWD impulse load.However,these models are defective in terms of engineering applications due to some disadvantages.For instance,the time calculation consumption of stiffness matrices method is a question due to the complicated transforms;the precision of finite-element model is restricted by calculation mesh size,i.e.,Focusing on acquiring high accuracy,large size memory and high efficiency are needed.

The precise integration method,which can obtain a precise numerical result,was presented by Zhong et al.[Zhong and Williams (1994)] and Zhong et al.[Zhong,Cheung and Li (1998)].It is a semi-analytical method to solve the first-order liner ordinary differential equations.This method not only avoids the computer truncation errors due to meticulous dividing,but also increases the numerical solution of matrix exponential to the accuracy of the computer.For this reason,it was quickly applied to solve the initial value problem of structural dynamics [Zhong,Williams and Bennett (1997)].On this basis,in combination with the simulation theory of optimal control and computational structural mechanics,Zhong et al.[Zhong,Lin and Gao (2004)] and Gao et al.[Gao,Zhong and Howson (2004);Gao,Lin,Zhong et al.(2006)] established a precise integration method for two-point boundary value problems.For linear time-invariant systems,both initial value and two-point boundary value problems,the precise integration method can give the exact solution with the computer,and it is almost independent of step size.After the precise integration method is put forward,it has been widely applied to structure dynamic response,the optimal control,random vibration,heat conduction,wave propagation,the complex dynamic elastoplastic analysis,dynamic load identification,and many other research fields.Lin et al.[Lin,Han and Li (2013,2014)] obtained the dynamic stiffness matrix of arbitrary-shaped rigid foundation supported on an isotropic or cross-anisotropic multi-layered soil by using the precise integration method.The precise integration method has following features:(1)It has extensive applicability for arbitrary horizontal multi-layered soil.There is no limitation to the layer number,thickness of layers and the material property.(2)It is with high efficiency for the matrices in the algorithm with small dimension.(3)The precise integration method used in the proposed method can ensure the high accuracy.In a sense,the accuracy of the proposed method only depends on the precision of computer applied.(4)The computation is always stable.

The objective of this paper is to simulate the behavior of the pavement structure based on the FWD dynamic test with the help of precise integration method and the mixed-variable formulation.The hybrid numerical method proposed in this paper can evaluate the dynamic response of the pavement structures subjected to the dynamic FWD loads.The numerical results can be compared with the deflection’s history measured by the FWD.The integral transform is used to obtain the displacement response in frequency domain.Then the results are expressed into rational function to construct a first-order ordinary differential equation.The latter can be solved accurately by the precise integration method.The dynamic numerical model proposed by this paper is closer to the physical reality of the pavement structures.The accuracy of the developed method has been demonstrated by comparison between the proposed method and published results from the other method.Then the proposed method is used to simulate the FWD test on a practical pavement structure as a forward calculation model.

2 Problem definition

Then,we study the forced steady state vibrations at the surface of a pavement structure.The describe wave motions in a multi-layered medium,a pavement structure consists of surface layer,road base and multi-layered soil foundation shown in Fig.1 is considered.A circular area of radiusais assumed to be subjected at the surface to a normal transient load.Allllayers as well as the half-space are defined as homogeneous and isotropic characteristic.The material properties are determined by Lame constantsλiandGi,mass densityρi,Poisson’s ratioνi,damping ratioξi(i=1,2,...,l).For convenience of calculation,a cylindrical coordinate system is established,and its origin is placed at the center of the circular area.The displacements at points 1,2,3 and so on along thexaxis can be evaluated by the following numerical method.

Figure 1:Schematic representation of the problem

Firstly,the displacement and stress vectors are expressed as following

withur,uθanduzrepresents the displacement components inr,θandzdirections in cylindrical coordinates respectively.τrzandτzθare the tangential stress components in the directions identified by the subscripts.σzis the normal stress component inzdirection.

For describing expediently,one individual layer is addressed in the following with the subscriptiis ignored.The advantage of the axisymmetric geometry of the circular area is taken to calculate the dynamic displacement response as shown in Fig.2.Then the displacement componentsur,uθanduzare decomposed into symmetric part and anti-symmetric part about ther-axis with a Fourier series as

The summation is performed over the integerα(α=0,1,2,...).And displacement components are the function of radialr,circumferentialθ,verticalzandα.The symmetric and anti-symmetric terms are denoted by the superscriptssandarespectively.

For the solution in frequency-spatial domain cannot been obtained directly,the problem is solved firstly in the frequency-wave number domain.The superscript bars of the symbols are referred to the function in frequency-wave number domain.Thus,the relationships for the displacement and stress vectors between the amplitudes in spatial and wave-number domain are established in Bessel transformation pairs as following [Kausel and Roësset (1981)]:

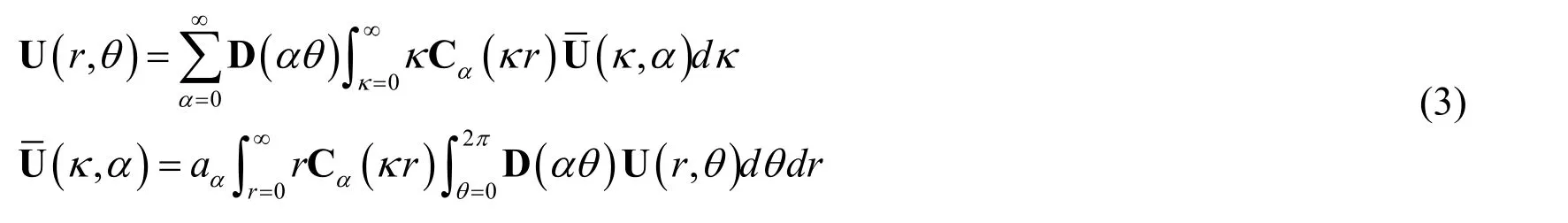
and

The wave-numberκin radial directionrruns from zero to infinitely.Therefore,every type of waves is included.The displacement and stress in the Eqs.(3)and (4)can be seen as an Fourier expansion in the circumferential directionθ.aαas normalization factor is an orthogonalization scalar.It is equal to 1 2πwhenαis equal to zero.Otherwise it is equal to 1π.The matrices D (αθ)and Cα(κr)are identified as

whereJα(κr)in the matrix Cα(κr)represents the Bessel function of orderαof the first kind.

The wave motion equation in cylindrical coordinate system can be expressed in the form of Lame equations as following

with

3 Solution in frequency-wave-number domain

For the evaluation of displacement during a circular area uniformly distributed load,the integernonly select as 0 and 1 in Eq.(2).The zeroth symmetric Fourier term (α=0)corresponding to a vertical distributed load acting on the circular area,while the first symmetric Fourier term is involved when a horizontal distributed load acting on the circular area in thexdirection [Kausel and Roësset (1981)].It is worth noting that the wave motion equation in Eq.(6)can be decoupled into two different plane waves:in-plane wave motion corresponding to P-SV wave and out-of-plane wave motion corresponding to SH wave [Zhang and Wolf (1985)].The differential equation of wave motion in Eq.(6)can be transformed from time domain into frequency domain by Fourier transform.Then it can be further transformed from spatial domain into wave-number domain.In the in-plane wave motion,the displacement(κ)is decoupled.The equation is only related to the displacements(κ)and(κ)as

The displacement(κ)is related to the out-of-plane wave as following

In the Eqs.(8)and (9),the subscript after the comma inrepresents differentiation with respect to vertical coordinatezand the rest can be inferred by analogy.Hereinafter,the differentiation with respect tozis rewritten as,that is

The two cases of Eqs.(8)and (9)can be unified into a general formula

with superscript 1m=and 2m=related to the P-SV wave and SH wave respectively.Imis a unit matrix.The coefficient matrices(i,j,m=1,2)are defined as (the superscriptHdenotes Hermitian transpose)

is the displacement vector.Form=1 andm=2 its expression are

The linear hysteretic material damping is used according to the principle.The Lame constantsλandGare replaced byλ( 1+2iξ)andG(1+2iξ)respectively with the damping ratioξ.It's pretty obvious that Eq.(10)is a second order ordinary differential equation which cannot be solved directly.Then a dual vector of displacement vectoris introduced to transform the Eq.(10)into a first order ordinary differential equation as given in Eq.(13).

The relationship between dual vectorand displacement vectorsatisfies

Then the Eq.(10)can be written as two first order ordinary differential equations as following

in which

Eq.(15)can be merged into one first order ordinary differential equation for briefly.

Zhong et al.[Zhong,Lin and Gao (2004)] presented an efficient and accurate method which is called precise integration method to solve the first order ordinary differential equation.

The stress vector should be equal to zero at the free surface (z=z0)as given in Eq.(18).

and at the interfaces between adjacent layers the vectorsandshould satisfy the continuity conditions as following

In addition,for the half-space soil,the radiation condition should be considered.The relationship between the stress and displacement vectors at the surface of the homogeneous isotropic half-space leads to [Zhong,Lin and Gao (2004)]

where

After the Eq.(17)is solved by precise integration method,the relationship between the tractions and the displacements at the surface of the pavement structure can be obtained combining with the boundary condition as the following form

The detailed forms of the Eq.(23)for the two cases 1m=and 2m=are

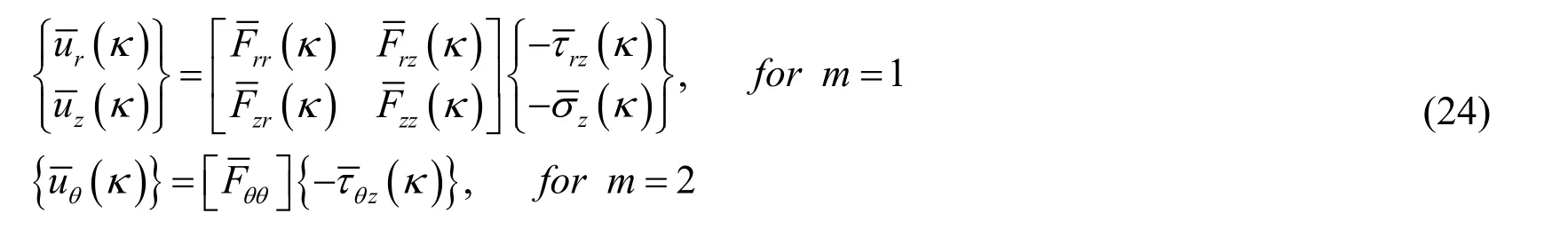
4 The displacement response in frequency-spatial domain

The displacements at the surface points of the pavement structure are evaluated for a circular area subjected to the vertical and horizontal uniformly distributed loads as shown in Fig.2.

Figure 2:Vertical and horizontal uniformly distributed loads (a:vertical;b:horizontal)

4.1 Vertical distributed load

The circular area of radiusais subjected by a vertical uniformly distributed load with amplitudepz0(Fig.2(a)).Only the zeroth symmetric Fourier term resulting in constant values around the circumference arises in Bessel transformation pairs.Then the load amplitude in frequency-wave-number domain can be formulated through Eq.(4)and (5)as following

Then the related horizontal and vertical displacement amplitudes are evaluated by Eq.(24)

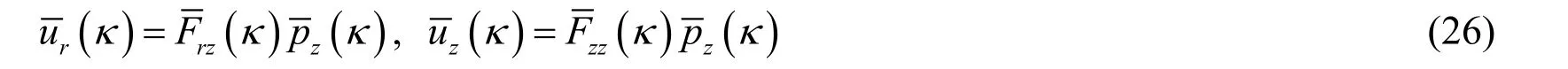
By using Eq.(3),the horizontal and vertical displacementur(r)anduz(r)can be transformed from wave-number domain into spatial domain as

Substituting Eqs.(26)into (27)leads to the displacement responses for the vertical load

4.2 Horizontal distributed load

Another consideration is that a distributed horizontal load acting on the circular area inx-direction,which is assumed to have the constant amplitudepx0as shown in Fig.2(b).Its radial and circumferential distributions arepx0cosθand-px0sinθ,respectively.Only the first symmetric Fourier term is considered in Eq.(2).By using Eq.(4)the amplitude of horizontal load in frequency-wave-number domain is evaluated as given in Eq.(29).

Then the related displacement in the radial,circumferential and vertical directions can be derived from Eq.(24)as

The inverse transformation of Eq.(30)leads to the displacementur(r,θ),uθ(r,θ)anduz(r,θ)in spatial domain according to the Eq.(3).Through a series of derivations,the formula for displacements in spatial domain are

For the circular area subjected by a uniformly distributed horizontal load with amplitudepy0in they-direction,the same formulas Eq.(31)are used,with cosθand-sinθsubstituted by sinθand cosθ,respectively.

The displacements at centers ofncircular areas are evaluated for these circular areas subjected to distributed loads in three directions by using Eqs.(28)and (31).Finally,the dynamic flexibility equation of the whole system can be assembled as following form

Eq.(32)can be rewritten in the following form for briefly.

The dynamic stiffness matrix S(ω) of the whole system can be evaluated by the inverse of the flexibility matrixuH as

5 The dynamic equation in time domain

The displacements in frequency domain is mainly used to analysis the essential dynamic properties of the pavement structure.However,the results obtained from FWD test is a curve of displacement over time.Usually,researches used the inverse Fourier transform which cannot ensure a high accuracy to obtain the time domain solution.Ruge et al.[Ruge,Trinks and Witte (2001)] presented a mixed-variable formulation to establish the dynamic equation in time domain by using the dynamic stiffness matrix S(ω) in frequency domain as given in Eq.(36).It is worth to note that all degrees of freedom of the dynamic stiffness matrix S(ω)are fully considered.As we obtain the discrete dynamic stiffness matric S(ω) by the proposed method in Sections 3 and 4,a matrix valued rational function is applied to interpolate the dynamic stiffness into a series of linear functions in iω.

where

A curve fitting technique is used to determine the coefficient matrices Rj(j=1,2,...,M+1)and Lj(j=1,2,...,M)which is based on the least square method.I is an identity matrix which has the same dimension as S(ω).Then the dynamic stiffness Eq.(35)can be expressed as

The rational function in (39)have a numerator degree+1Mand a denominator degreeM.Hence,it can always be divided into a linear function in iωand another rational function of numerator degree (M-1).In the next step,a new internal variable is defined by the division process.As a result,the rational function is rewritten in a series of equations with different variables.These variables are combined into a mixed-variable which includes not only displacements but also forces.Thereafter,the dynamic equation of the whole system in time domain is established which is a first order ordinary differential equation.

where A and B can be calculated by matricesRjandLj.The detailed solution process can refer to Ruge et al.[Ruge,Trinks and Witte (2001)].In additional,the number of degrees of freedom of Eq.(40)is increased to 3n×(M+1)instead of the degrees of freedom of matrix S(ω) which is 3n.The dynamic equation in time domain (Eq.(40))can be solved by precise integration time history method numerically.

6 Solution in time domain

From the theory of linear ordinary differential equations,we need to solve the general solution of the homogeneous equation first,and then combine it with the superposition principle to find the particular solution of the inhomogeneous equation.So,we remove the inhomogeneous term f (t)first from Eq.(40),and then it is converted to the following:

As the matrix H is a constant matrix,the solution to Eq.(41)is the exponential form,as follows:

If the length of the time step for the solution isγ,then

Thus,if the matrix T can be solved,then the schedule of integral becomes

Expressing the matrix T in the following form:

In order to facilitate the interval merge operation of the fine integration algorithm,υneeds to be equal to 2,such as 2N0,whereN0is an integer.For structure-ground-based dynamic interaction problems,the time intervalγis small,soε γ υ=is very small.Thus,for the interval periodε,the exponential function can be calculated using a Taylor series expansion.Based on experience,in order to obtain sufficient accuracy,it is necessary to use the fourth order Taylor series,as follows:

Sinceεis very small,the absolute values of the terms inare also small.When calculating the storage,it is easy to lose the effective number when adding the unit matrix.

The solution of Eq.(45)can be calculated using the following algorithm:

It can be seen that Eq.(47)is only given0Ntimes to get the final matrix T.First of all,the matrix multiplication gives InN0cycles,every time whenis computed gives a new.Hence,afterN0cycles,the sum of finaland I is the final matrix solution of T.

Assuming that the inhomogeneous terms of f (t)is linear within the time step,Eq.(41)can then be written as follows:

with β-1f (t)=η0+η1(t-tl)

Eq.(49)can be solved using the superposition principle.The solution T of the homogeneous Eq.(41)is obtained previously in Eq.(47),and the solution of the inhomogeneous equation is as follows:

7 Numerical examples

In this section,two different examples are presented to illustrate the proposed method.The first example is given to verify the accuracy and capacity of this method,and a pavement structure including four different layers is considered.The second example is provided to simulate the FWD test for a practical pavement structure which can prove the applicability of the proposed algorithm.

7.1 Verification

In this example,a pavement structure consists of three layers underlain by a homogeneous subgrade is considered.The material properties for each layer and subgrade are given in Tab.1,including Lame constantsλiandGi,Poisson’s ratioνi,densityρi,thicknesshiand damping ratioξi.The FWD load is applied over a circular area at the surface of the pavement structure with a radius of 15 cm.The load-time curve is provided in Fig.3 which has a magnitude of 40 kN.The displacements were evaluated at radial distances of 0,30,60,90,120,150 and 200cm from the center of the load area.The maximum displacements for every point obtained by the proposed method are shown in the Fig.4.And the displacements at radial distances of 0cm are presented over time in Fig.5.All these results are compared with the reference solution obtained by Simon et al.[Simon,Jean-Marie and Denis (2009)].As the figures shown,the agreement is excellent perfect,and the proposed approach proved to be accurate and capable.

Table 1:The material properties of the pavement structure

Figure 3:Load-time curve

Figure 4:The maximum displacements along the radial distance

Figure 5:Displacements at radial distances of 0 m

7.2 FWD test simulation

Table 2:Material properties for multi-layered half-space

Figure 6:Load-time curve

A practical pavement structure in Henan province,China,including 100 mm thick surface layer,a 300 mm thick subbase rests on the subgrade is considered in this numerical example.The material properties for each layer and half-space of this practical pavement structure are provided in Tab.2.The dynamic FWD test load is captured from the sensor on the falling weight deflectometer with a magnitude of 52.52 kN (Fig.6).The duration of the FWD load is 60 ms.The same as the first example,the FWD load is applied over a circular area with a radius of 15 cm.The displacements of basins are evaluated at radial distances of 0,30,60,90,120,150 and 180 cm from the center of the load area.A comparison between the measured data from the dynamic FWD test and results calculated by the proposed method is made to verify the applicability of the proposed method to simulate the dynamic FWD test.The maximum displacements for every point evaluated by the proposed method is compared with the measured results in Fig.7.As we can see from the figure,the agreement is very good between two sets of results.Only the maximum displacements of the measured results at radial distance of 0.3,0.9 and 1.2 is smaller than the results obtained by the proposed method.And the difference is no more than 30%.The reason for the difference may be due to data collection during the FWD test.The displacements at radial distances of 0cm evaluated by proposed method are plotted versus time in Fig.8 which is also compared with the measured results.There is an excellent agreement between the two results at the rising section of the curve,especially for the peak value.However,the descent section of the curve displays different behaviors.The results obtained by proposed method is falling faster than the measured results.The results show that the proposed method can be used as a forward calculation model to simulate the dynamic FWD test on a multi-layered pavement structure.

Figure 7:The maximum displacements along the radial distance

Figure 8:Displacements at radial distances of 0.0 m

8 Conclusion

A hybrid numerical method is developed to calculate the dynamic displacement response of the pavement structure based on the integral transformation and mixed variable technique.Comparison with spectral element method for a multi-layered pavement structure subjected to an impulse load,the proposed method has shown to be accurate and capable.Furthermore,a comparison for a practical pavement structure between the results obtained by the proposed method and the measured data from a dynamic FWD test proves the proposed method is accurate.All the results show that the proposed methodology can be used as a forward tool for the simulation of wave propagation in a multi-layered pavement structure.

Acknowledgements:The authors are grateful for the financial support of the National Key Research and Development Program of China (No.2016YFC0802400),the National Natural Science Foundation of China under Grant No.(51508203,51678536,41404096),the Outstanding Young Talent Research Fund of Zhengzhou University (1621323001),Program for Innovative Research Team (in Science and Technology)in University of Henan Province (18IRTSTHN007 ),the Program for Science and Technology Innovation Talents in Universities of Henan Province (Grant No.19HASTIT043),and the authors extend their sincere gratitude.