一类特殊三色有向图的本原条件和指数上界

罗美金，欧阳云

(河池学院数学与统计学院，广西 宜州 546300)

若D是包含红弧、黄弧和蓝弧的有向图，则称D是一个三色有向图。若D中每一对顶点(i,j)都存在从i到j的途径，则称三色有向图D是强连通的，给定D中的一条途径ω，用r(ω)、y(ω)和b(ω)分别表示ω中红弧、黄弧和蓝弧的条数，称ω为一条(r(ω),y(ω),b(ω))-途径，ω的分解为向量(r(ω),y(ω),b(ω))或(r(ω),y(ω),b(ω))T[1]。

一个三色有向图D是本原的，当且仅当存在非负整数h、k和v，且h+k+v>0，使得D中的每一对顶点(i,j)都存在从i到j的(h,k,v)-途径，h+k+v的最小值定义为三色有向图D的本原指数，记为exp(D)[1]。

设D中含有圈γ1,γ2,…,γl，C={γ1,γ2,…,γl}是D的圈集合，定义D的圈矩阵M是一个3×l矩阵，它的第i列是γi圈的分解。M的content(记为content(M))定义为0，如果M的秩小于3，否则定义为M所有非零3阶主子式的最大公因数[2]。

引理1[1]一个至少包含1条红弧、1条黄弧和1条蓝弧的三色有向图D是本原的，当且仅当D是强连通的，且content(M)=1。

图1 未着色三色有向图Dn,4,2

根据矩阵与有向图的对应关系，非负矩阵簇也可以与其伴随有向图(即多色有向图)建立一一对应关系。当前，国内外关于多色有向图的本原指数已经取得一些成果[1～5]，笔者研究了一类含有n(n≥5，且n为奇数)个顶点，包含3个圈，且至少包含1条红弧、1条黄弧和1条蓝弧的三色有向图Dn,4,2,其未着色有向图如图1所示。结合图1可得，Dn,4,2是强连通的，对任意的D∈Dn,4,2，D中恰包含1个n-圈、1个4-圈和1个2-圈，且3个圈有唯一的一条公共弧n→1。由引理1得，D若本原，则content(M)=1，即det(M)=±1。容易验证，2-圈中的2条弧若着相同颜色，即着色为(2,0,0)T，(0,2,0)T或(0,0,2)T时，则det(M)≠±1，即D是不本原的。因此，D若本原，2-圈中的2条弧必含2种颜色，不妨设2-圈的着色为(1,1,0)T。同理，容易验证，当2-圈的着色为(1,1,0)T,且4-圈中着色为(4,0,0)T，(0,4,0)T(0,0,4)T，(2,2,0)T，(2,0,2)T，(0,2,2)T， (1,1,2)T，(1,3,0)T或(3,1,0)T时，则det(M)≠±1，即D是不本原的。因方法类似，以下只考虑4-圈中至少包含1条红弧、2条蓝弧和1条黄弧的情形，且设D的圈矩阵为：

其中x,y都为非负整数。

1 本原条件

定理1 若任意的D∈Dn,4,2是本原的，且4-圈的着色为(1,2,1)T，则-n+2y=±1。

证明 显然，图1所示的有向图D是强连通的，根据引理1得，若D是本原的，当且仅当content(M)=1，即det(M)=±1，而此时所对应的圈矩阵为M，det(M)=-n+2y。因此，D若是本原的，即-n+2y=±1。

2 指数上界

定理2 若任意的D∈Dn,4,2是本原的，且4-圈的着色为(1,2,1)T，则：

证明 对D中的任意一对顶点(i,j)，记pij是从i到j的最短路，r(pij)=s，y(pij)=t，b(pij)=w。结合定理1，分以下2种情形讨论：

情形1：-n+2y=1。此时，所对应的逆矩阵M-1为：

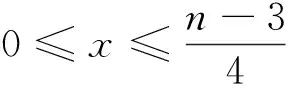
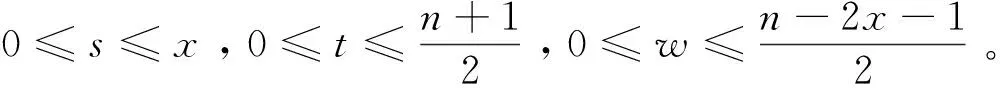
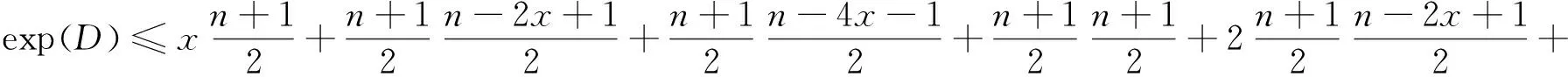
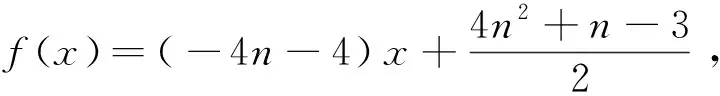
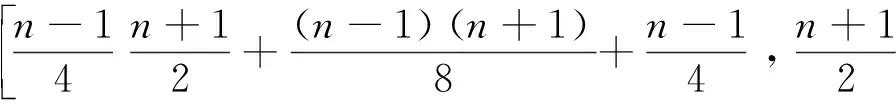
=n2+n-1

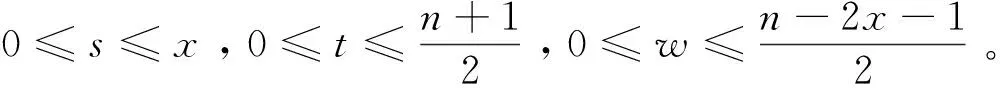
情形2：-n+2y=-1。此时所对应的逆矩阵M-1为：