应用半单连分数求解Pell方程

高 升

(合肥工业大学 数学学院，安徽 合肥 230601)

引 言

为方便讨论,先引入一些记号和定义。本文提到的整数,均为有理整数。表示全体整数之集，+表示全体正整数之集，≥0表示全体非负整数之集，表示全体有理数之集。两个整数a和b的最大公因子记作g.c.d.(a,b)。对任一实数x，“[x]”表示不超过x的最大整数。

特别地，当a0∈，a1,a2,a3,…∈+时，称「a0,a1,a2,…,an」为有限简单连分数，称「a0,a1,a2,……」为无限简单连分数；当a0∈而a1,a2,a3,…为大于1的整数时，称「a0,a1,a2,…,an」为有限半单连分数，称「a0,a1,a2,……」为无限半单连分数。

(1)若存在m∈≥0和k∈+，使得∀n≥m，都有an+k=an，则称为循环数列，称无限连分数「a0,a1,a2,……」或「a0,a1,a2,……」为循环连分数，称k为该数列或该连分数的周期，此时将该连分数记为或

(2)若存在k∈+，使得∀n≥0，都有an+k=an，则称为纯循环数列，称无限连分数「a0,a1,a2,……」或「a0,a1,a2,……」为纯循环连分数。

设Δ∈+非完全平方数，则可以用的无限简单连分数展开式的渐近分数给出Pell方程x2-Δy2=±1的基本解(即最小正解)和全部正整数解。这是数论中广为人知的经典结果(参见专著[2]的第3章第3节，[4]的第7章第6节，或者[5]中的定理3.18)。

对于在实二次域理论中应用广泛的Pell方程x2-Δy2=4，求解过程更复杂。根据[3]中第1章引理2.4，如果非完全平方的正整数Δ=b2+4ac，其中a,b,c∈，|b|ac，g.c.d.(a,b,c)=1，那么可以用的无限简单连分数展开式的渐近分数给出方程x2-Δy2=4的最小正解和全部正整数解。困难的地方在于，此时必须讨论的无限简单连分数展开式的最小周期的奇偶性。在最小周期为奇数和最小周期为偶数这两种情况下，方程x2-Δy2=4的解的情况存在较大差异。

本文将以二次无理数的无限半单连分数展开式为工具给出Pell方程x2-Δy2=4的最小正解和全部正整数解。这种方法的优点是无需讨论最小周期的奇偶性，在各种情况下都有统一的表达式。

1 预备知识

为了便于应用，将半单连分数的基本性质列举如下(这些性质都是已知的，可以在[1]，[5],[6]中找到)。

引理2.1 设x1,…,xn为实数。若xj≥2(1j1，则「x1,…,xn」>1。

s-2=0，s-1=1，t-2=-1，t-1=0；sn=xnsn-1-sn-2，tn=xntn-1-tn-2，∀n≥0；

又设a∈，则以下结论成立(假定其中出现的各连分数和分数都有意义)：

(1)∀n∈+,∀r∈≥0,有「x0,…,xn-1,xn,…,xn+r,a」=「x0,…,xn-1,「xn,…,xn+r,a」」；

(2)∀n∈≥0，有(约定：当n=0时，等式左边就表示a)；

(3)∀n∈≥0，有

引理2.3(半单连分数的基本运算性质)(假定其中出现的各连分数和分数都有意义)

(1)∀n∈+，有

(2)设a,b∈，n∈≥0，则且

(3)设k∈+，a2,a4,…,a2k-2∈，a1,a3,…,a2k-1∈+，则有

(1)∀n∈≥0，∀δ∈[1,+)，∀ε∈(0,+)，都有「x0,…,xn,δ」<「x0,…,xn,δ+ε」；

(2)∀n∈≥0，都有「x0,…,xn」>「x0,…,xn,xn+1」>x0-1；

引理2.5(半单连分数展开式的存在性和唯一性)

(i)∀j≥1，有aj≥2；

(ii)∀j≥0，有ξj=「aj,aj+1,aj+2,aj+3,…」；

(iii)ξ=「a0,a1,a2,a3,…」(即任一实数都可展开为无限半单连分数)；

(i)∀n≥0，有an=[θn]+1，且θ=「a0,…,an-1,θn」；

(ii)∀n≥1，有θn≥1；

(iii)θ为有理数的充要条件是：存在j0≥0，使得aj=2(∀j≥j0)；

(iv)θ为无理数的充要条件是：集合{j∈|j≥0,aj≥3}含无限多个元素。

引理2.6 设ξ为无理数且ξ=「a0,a1,a2,a3,…」，其中aj∈(∀j≥0)，且aj≥2(∀j≥1)，则ξ为二次无理数的充要条件是：存在m∈≥0和k∈+，使得∀n≥m，有an+k=an。

引理2.7 设ξ为实二次无理数，则ξ可表示为无限纯循环半单连分数的充要条件是：ξ>1且ξ的共轭数属于开区间(0,1)。

以下命题是初等的，但对于本文主要定理的证明很有用。

证明 若已知g.c.d.(u1,v1)=1，则存在λ,μ∈，使得λu1+μv1=1，即于是，由已知条件可知即(r11λ+r12μ)u+(r21λ+r22μ)v=1，从而必有g.c.d.(u,v)=1。

3 本文主要结果及其证明

引理3.1 若a,b,c∈，|b|ac，且Δ=b2+4ac非完全平方数(此时当然有a≠0且c≠0)，则必存在a0,a1,…,ak∈，其中a1,…,ak≥2，使得

由引理2.3(4)可以推出以下结论。

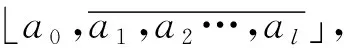
(1)若l=2k(其中k∈+)，则α可表示为无限循环半单连分数

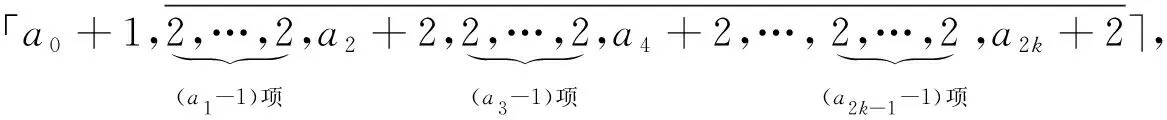
(2)若l=2k-1(其中k∈+)，则α可表示为无限循环半单连分数

以下定理将该恒等式推广到无限循环半单连分数的情形，系本文的原创。

(sk-1+βtk-1)m=smk-1+βtmk-1。

(1)

证明 由已知条件可知，存在整系数二次多项式ax2-bx-c(其中a,b,c∈，a>0)，使得ax2-bx-c=a(x-α)(x+β)。此时,有

由已知条件，可知s0=a0，t0=1。再由半单连分数的渐近分数的性质(引理2.2)可知，∀n≥1，都有sn=ansn-1-sn-2，tn=antn-1-tn-2。

∀m≥0，有α=「a0,…,amk,amk+1,amk+2,amk+3,amk+4,……」

=「a0,…,amk,a1,a2,a3,a4,……」

=「a0,…,amk,「a1,a2,a3,a4,……」」

(2)

下面运用对m的归纳法来证明(1)式，即(sk-1+βtk-1)m=smk-1+βtmk-1(∀m≥0)。

当m=0时结论显然成立。

假设(1)式对非负整数m成立，我们分两种情况来证明它对m+1仍然成立。

第一种情况，设k=1。此时sk-1=s0=a0，tk-1=t0=1。由归纳假设，有

(s0+βt0)m=(a0+β)m=sm-1+βtm-1，从而

(s0+βt0)m+1=(a0+β)m+1=(a0+β)m(a0+β)

=(sm-1+βtm-1)(a0+β)

=a0sm-1+β(a0tm-1+sm-1)+tm-1β2

=sm+βtm(由(2)式)，

所以此时(1)式对m+1仍然成立。

第二种情况，设k≥2。此时我们有

=「a0,…,amk,「a1,a2,…,ak-1」」

所以，由既约分数的性质可知

smktk-1+smk-1(sk-1-a0tk-1)=s(m+1)k-1，tmktk-1+tmk-1(sk-1-a0tk-1)=t(m+1)k-1。

(3)

于是，我们有

(sk-1+βtk-1)m+1=(sk-1+βtk-1)m(sk-1+βtk-1)

=(smk-1+βtmk-1)(sk-1+βtk-1)(由归纳假设)

=smk-1sk-1+β(smk-1tk-1+tmk-1sk-1)+β2tmk-1tk-1

=smk-1sk-1+(smk-a0smk-1)tk-1+β[(tmk-a0tmk-1)tk-1+tmk-1sk-1](由(2)式)

=s(m+1)k-1+βt(m+1)k-1(由(3)式)，

即(1)式对m+1仍然成立。

推论3.4 设实二次无理数α=「a0,a1,a2,a3,……」=「b0,b1,b2,b3,……」，其中a0,b0∈，和都是正整数列，且bj≥2(∀j≥1)；又设∀n≥1，有an+l=an和bn+m=bn，且l和m分别为循环简单连分数「a0,a1,a2,a3,……」和循环半单连分数「b0,b1,b2,b3,……」的最小周期。设β为α的共轭数的相反数，又设其中p,s∈，q,t∈+，g.c.d.(p,q)=g.c.d.(s,t)=1，则以下结论成立：

(1)当l为偶数时，必有s+βt=p+βq；

(2)当l为奇数时，必有s+βt=(p+βq)2。

(1)设l=2k(k∈+)。由引理3.2(1)可知，

=「a0,a1,a2,a3,…,a2k-1」(由引理2.3(3))

由既约分数的性质可知s=p，t=q，从而s+βt=p+βq。

(2)设l=2k-1(k∈+)。由引理3.2(2)可知，

=「a0,a1,a2,a3,…,a2k-1,a1,a2,a3,a4,…,a2k-2」(由引理2.3(3))

=「a0,a1,a2,a3,…,a2k-1,a2k,a2k+1,a2k+2,a2k+3,…,a4k-3」

所以s=p2l-1且t=q2l-1，进而s+βt=p2l-1+βq2l-1=(pl-1+βql-1)2=(p+βq)2。

以下定理是本文的主要结果，用无限循环半单连分数的渐近分数给出了一类在代数数论中有重要应用的Pell方程的最小正解和全部正整数解。

定理3.5 设a,b,c∈，|b|ac，g.c.d.(a,b,c)=1，且Δ=b2+4ac非完全平方数。记设α的无限半单连分数展开式为「a0,a1,a2,a3,…」，它的最小周期为k，其中为整数列，当j≥1时恒有aj≥2。对每个n≥0，设「a0,a1,…,an」=sn/tn，其中sn∈，tn∈+，g.c.d.(sn,tn)=1，则以下结论成立：

(1)Pell方程x2-Δy2=4的最小正解为sk-1+βtk-1；

(2){(x,y)∈+×+|x2-Δy2=4}

证明 设α的无限简单连分数展开式为「A0,A1,A2,A3,……」，最小周期为h，其中A0∈，Aj∈+(∀j≥1)。由[3]中第1章引理1.2可知，必有对每个m≥0，令「A0,A1,…,Am」=pm/qm，其中pm∈，qm∈+，g.c.d.(pm,qm)=1。

(2)这可以从[3]中第1章引理2.2和本文的定理3.3直接推出。

致谢

作者感谢赵立璐教授对本文引理3.2提供的帮助。