F－Gorenstein平坦维数

刘 苗， 杨晓燕

(西北师范大学数学与统计学院，甘肃兰州730070)

自Enochs等引入Gorenstein投射、内射和平坦模的概念［1－2］以来，受到许多学者的关注，见文献［3－6］．在Holm［5］引入了相应的Gorenstein同调维数之后，Gorenstein同调代数理论完全建立．

Holm在文献［5］中证明了Gorenstein投射模类在一般环上是投射可解的，并且每个具有有限Gorenstein投射维数的模具有特殊的Gorenstein投射预覆盖．但在一般的环上，Gorenstein平坦模类是否是投射可解的，到目前尚未可知．为了在平坦模的纯导出范畴中研究Tate以及完全上同调理论，Asadollahi等在文献［3］中引入了F－Gorenstein平坦R－模的定义．Hu等在文献［6］中证明了 F－Gorenstein平坦模类是投射可解的，并且在凝聚环的情形下与Gorenstein平坦模类一致．本文的主要目的是进一步研究F－Gorenstein平坦模类的同调性质．

1 F－Gorenstein平坦模

本文中的环R指有单位元的结合环，模都是酉模，用R－Mod表示左R－模范畴．文中所说的模类是指R－Mod中在同构封闭下的全子范畴．用P、F和C分别表示所有投射、平坦和余挠左R－模构成的模类，用pdR(M)和fdR(M)分别表示左R－模M的投射和平坦维数．

定义 1．1 设X是左R－模类．1)称R－Mod中的正合序列

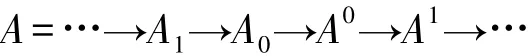
是HomR(－，X)－正合的，如果对任意的 X∈X，序列HomR(A，X)是正合的．

2)称M∈⊥X，如果对任意的X∈X，有

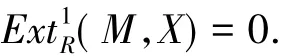
类似地，可以定义M∈X⊥．

定义 1．3 设A、B是左R－模类．

1)称(A，B)是余挠对，如果A⊥=B且

⊥B=A．

2)称余挠对(A，B)是遗传的，如果对任意的A∈A，B∈B，ExtiR≥1(A，B)=0．

3)称余挠对(A，B)是完备的，如果对任意的左R－模M，存在短正合列

其中A∈A，B∈B;等价地，存在短正合列

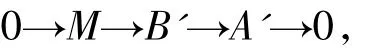
其中 A'∈A，B'∈B．

众所周知，(F，C)形成完备遗传的余挠对．

定义 1．4［1］称左 R－模 M 是Gorenstein平坦的，如果存在一个平坦左R－模构成的正合序列

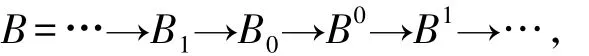
使得

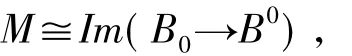
定义 1．5［3］称左 R－模 M 是 F－Gorenstein 平坦的，如果存在平坦左R－模构成的正合列

使得

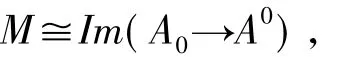
并且对任意X∈F∩C，HomR(A，X)是正合的(这样的正合列A也简称为HomR(－，F∩C)－正合列)．

以下用G(F)表示Gorenstein平坦左R－模类，用H(F)表示F－Gorenstein平坦左R－模类．

下述引理见文献［6］中的引理3．2 和引理3．4．

引理1．6 设M是左R－模，则以下条件等价:

1)M是F－Gorenstein平坦左R－模;

2)M∈⊥(F∩C)，且存在HomR(－，F∩C)－正合的正合列

其中每个Ai∈F∩C．

若R是右凝聚环，则上述的条件也等价于:

3)M是Gorenstein平坦左R－模．

注 1．7 由引理1．6易知，每个F－Gorenstein平坦R－模都有特殊的F∩C－预包络．

下述结论见文献［6］中的命题3．7．

引理1．8 模类H(F)是投射可解的，并且H(F)对任意的直和与直和项封闭．

2 F－Gorenstein平坦维数

引理 2．1 设M是左R－模，

与

是左 R－模正合列，其中 Gi，Hi∈H(F)，i=0，1，…，n－1，则 Gn∈H(F)当且仅当 Hn∈H(F)．

证明 作第三个正合序列

其中每个Pi∈P．由比较引理可得如下的交换图:

由此可得如下映射锥正合序列

由于 Gi，Pi∈H(F)，所以由引理 1．8 知

PiGi+1∈H(F)， 0≤i≤n－2．

于是有K∈H(F)当且仅当Gn∈H(F)．

对第二个正合列作相应的论断，于是也有K∈H(F)当且仅当Hn∈H(F)．由此得到 Gn∈H(F)当且仅当Hn∈H(F)．

定义 2．2 设R是环，M 是左R－模．若有正合列

其中 F0，F1，…，Fn是 F－Gorenstein 平坦模，则称该正合列是M的一个有限F－Gorenstein平坦分解，其中n称为此F－Gorenstein平坦分解的长度．令F－GfdR(M)=inf{n|M有长度为n的F－Gorenstein平坦分解}，

称之为模M的F－Gorenstein平坦维数．若M不存在上述形式的F－Gorenstein平坦分解，则规定

F－GfdR(M)=∞．

回顾左R－模M称为Gorenstein投射的，如果存在投射左R－模构成的HomR(－，P)－正合的正合列

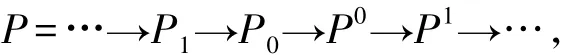
使得

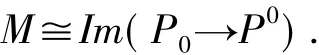
用G(P)表示所有Gorenstein投射左R－模构成的类．

注 2．3 1)设R是右凝聚环，则由引理1．6知从而对任意的左R－模M，其中GfdR(M)表示左R－模M的Gorenstein平坦维数．

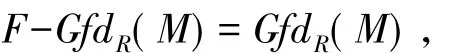
2)设R满足P=F∩C，则由文献［6］中的命题3．5 可知H(F)=G(P)，从而其中GpdR(M)表示左R－模M的Gorenstein投射维数．

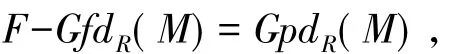
引理 2．4 设是左R－模的短正合列，其中 F'，F∈H(F)．若对任意的 X∈F∩C，有

则M∈H(F)．

证明 因为 F'∈H(F)，所以由引理1．6可知存在左R－模的正合序列

其中 Q∈F∩C，L∈H(F)．作推出图:

因为 F∈H(F)且 L∈H(F)，所以 H∈H(F)．用HomR(－，Q)作用于第二行的短正合列，得到正合序列

注意到Ext1R(M，Q)=0，故第二行的短正合列可裂，所以M∈H(F)．

注 2．5 设

是左R－模中的短正合序列，其中F∈H(F)，则有

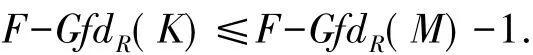
用珘F表示平坦维数有限的左R－模构成的类．引理 2．6 设M是左R－模，且则以下条件等价:

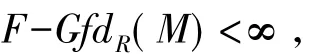
1)M是F－Gorenstein平坦模;

2)对任意的i＞0及任意的X∈F∩C，有

3)对任意的i＞0及任意的X∈珘F∩C，有

下面对m进行数学归纳．若m=0，则由2)知对任意 i＞0，有Exti

R(M，X)=0．

设m＞0，考虑短正合序列

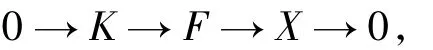
其中 F∈F，K∈C，则fdR(K)≤m－1．从而由归纳假设可知，对任意的 i＞0，ExtiR(M，K)=0．另一方面，由于 X，K∈C，于是由 2)可知，对任意的 i＞0，有

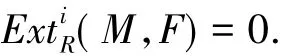
因此，由正合列

可知，对任意的 i＞0，有

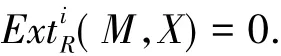
于是存在左R－模的短正合列

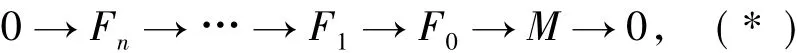
其中每个Fi∈H(F)．将(*)打断成如下短正合列

其中 Kn－1=Fn，C0=M．考虑短正合列

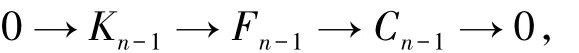
设Y∈F∩C，则由维数转移可得

由于 Kn－1，Fn－1∈H(F)．从而由引理 2．4 可知，Cn－1∈H(F)，对其余短正合列重复该论断，可以得到每个Ci∈H(F)．特别地，M∈H(F)．

下述引理给出了F－Gorenstein平坦维数的刻画．

引理 2．7 设n是非负整数，M是左R－模，且

则以下条件等价:

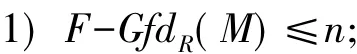
2) 对任意的i＞n，及任意的X∈F∩C，有

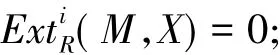
3)对任意的i＞n，及任意的X∈珘F∩C，有

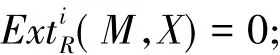
4) 设0→Kn→Fn－1→…→F0→M→0 是左 R－模正合列．若每个 Fi∈H(F)，则 Kn∈H(F)．

其中每个Fi∈H(F)．对任意的左R－模

由于Fn∈H(F)，由维数转移和引理2．6得

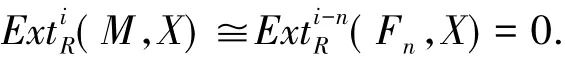
故由引理2．6得到Kn∈H(F)．

以下定理为本文的主要结论．

定理 2．8 设M是左R－模，且

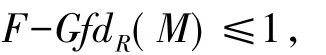
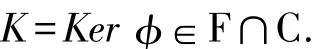
证明 考虑R－Mod中的短正合列

其中 F∈F，K'∈C．由F－GfdR(M)≤1 及引理 2．7 可知K'∈H(F)．从而由引理1．6可知存在短正合列

其中H∈F∩C，C∈H(F)．作推出图:

由于在中间列的短正合列中F，C∈H(F)，从而Q∈H(F)．考虑短正合序列

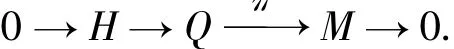
由于对任意的Q'∈H(F)，有

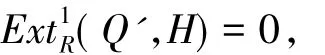
从而π:Q→M是M的特殊的F－Gorenstein平坦预覆盖．

定理 2．9 设M是左R－模，则

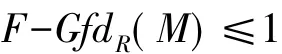
当且仅当存在左R－模的正合列

其中 A∈H(F)，H∈C，且fdR(H)≤1．

证明 充分性 由于H∈C且fdR(H)≤1，从

而存在短正合序列

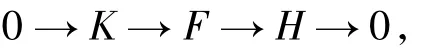
其中K，F∈F∩C．作如下拉回图:

由第二行短正合序列及H(F)的投射可解性可知，Q∈H(F)．所以由第一列短正合列可知

必要性 由定理2．8可知，存在左R－模的短正合列

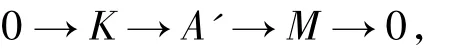
其中 A'∈H(F)，K∈F∩C．由 A'∈H(F)可知，存在左R－模的短正合列

其中Q∈F∩C，A∈H(F)．因此，有如下推出图:

考虑短正合列

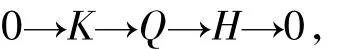
由于 K，Q∈F∩C，从而

就是所需的短正合列．

定理 2．10 设环R满足每个模的F－Gorenstein平坦维数不超过1，则(H(F)，Y)是完备遗传的余挠对，其中

Y={Y∈R－Mod|Y∈C 且 fdR(Y)≤1}．

证明 先证(H(F)，Y)形成余挠对．由引理2．7可知，对任意的X∈H(F)及任意的 Y∈Y，有Ext1R(X，Y)=0．设左R－模X 满足对任意的Y∈Y，有Ext1R(X，Y)=0．由于F－GfdR(X)≤1，所以由定理 2．8 可知，存在如下的短正合列

其中 K∈F∩C，G∈H(F)．从而Ext1R(X，K)=0，这说明短正合列(#)可裂，因此X同构于G的某个直和项，于是由引理1．8可知X∈H(F)．

设左R－模Y满足对任意的X∈H(F)，都有Ext1R(X，Y)=0．由于F－GfdR(Y)≤1，所以由定理 2．9可知，存在短正合列

其中 H∈Y，且 A∈H(F)．于是

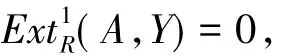
综上所述，(H(F)，Y)形成余挠对．由引理1．8知该余挠对是遗传的．由于

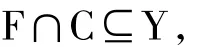
所以由定理2．8知该余挠对是完备的．