对一道预赛试题的进一步探究

(邮编：244000)

安徽省铜陵市第一中学

1 原题再现

(1)试题(2018山西省预赛第10题)

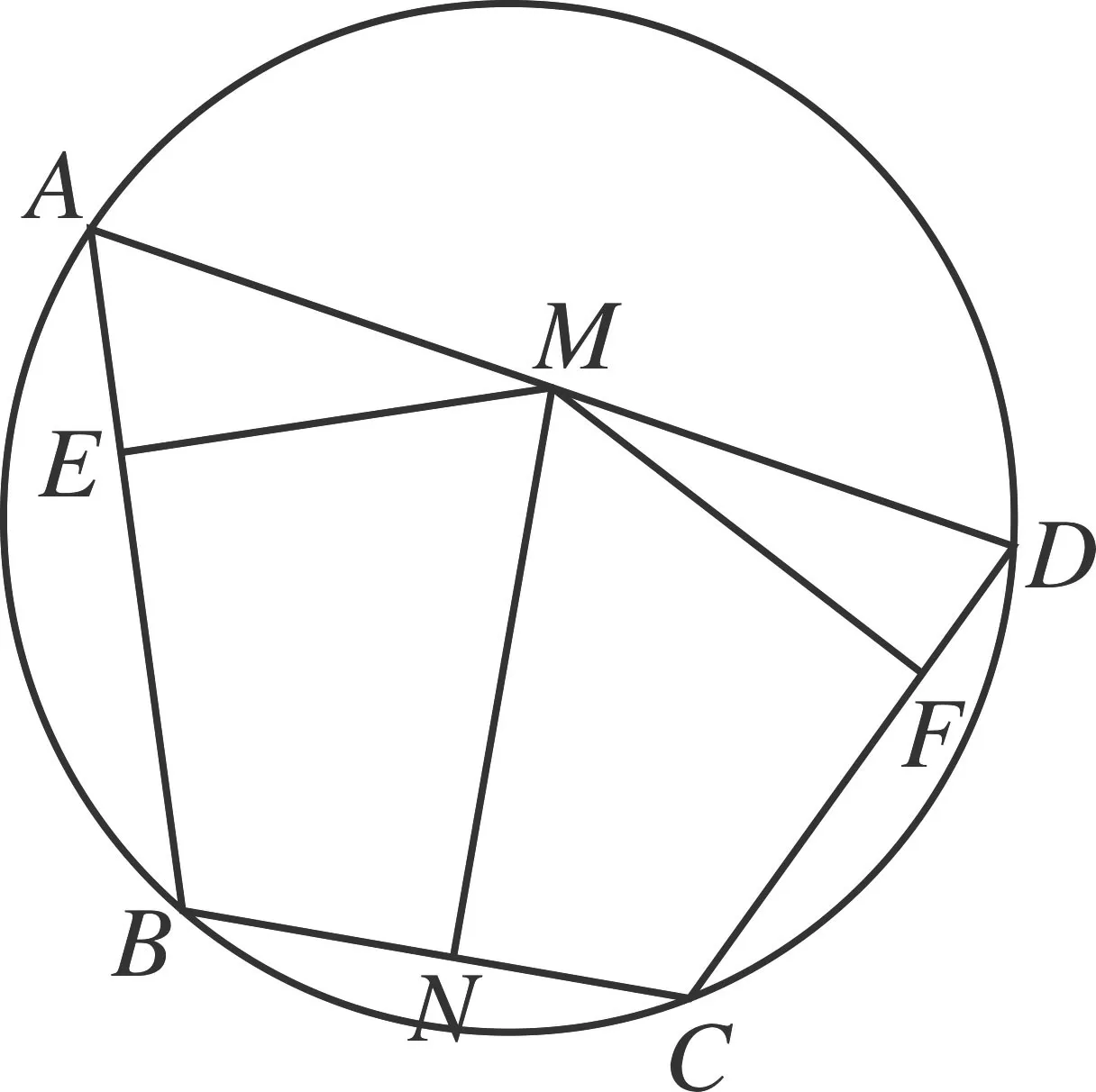
图1

如图1，圆内接四边形ABCD中，自AD的中点M作MN⊥BC，ME⊥AB，MF⊥CD，N、E、F为垂足.

证明：MN过线段EF的中点.

(2)参考解答

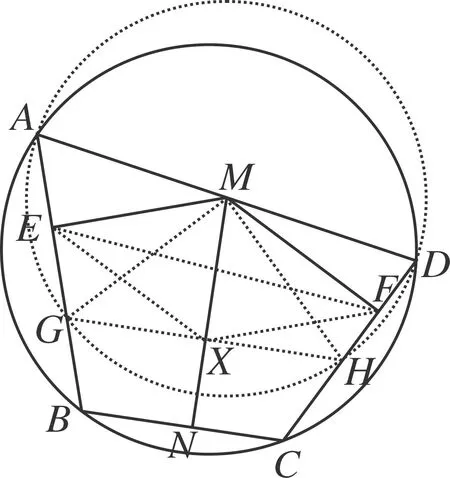
图2

如图2，在线段AB、CD上分别取点G、H，使AE=GE,DF=HF，则A、G、H、D四点共圆(以M为圆心)，所以∠BGH=∠ADC=180°-∠ABC，于是GH//BC，则MN⊥GH，设垂足为X，于是X为GH的中点.这样就有E、X、F、M为四边形AGHD四条边的中点，因此EXFM为平行四边形，故其对角线相互平分，即MN过线段EF的中点.

2 其它解法

思路1 证明交点即中点

图3

如图3，连接EF交MN于点K，证出EK=KF共线即可.

首先注意到E、B、N、M与A、B、C、D四点共圆，

所以∠EMN=180°-∠B=∠D.同理∠FMN=180°-∠C=∠A.

在这样的思路指引下，可设计出如下解法.

解法一 (面积法)

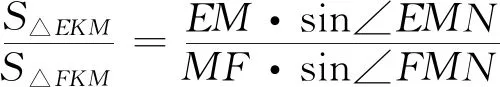
解法二 (正弦定理)

在△EMK中，由正弦定理得

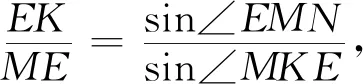
所以EK=KF.

解法三 (相似与全等)

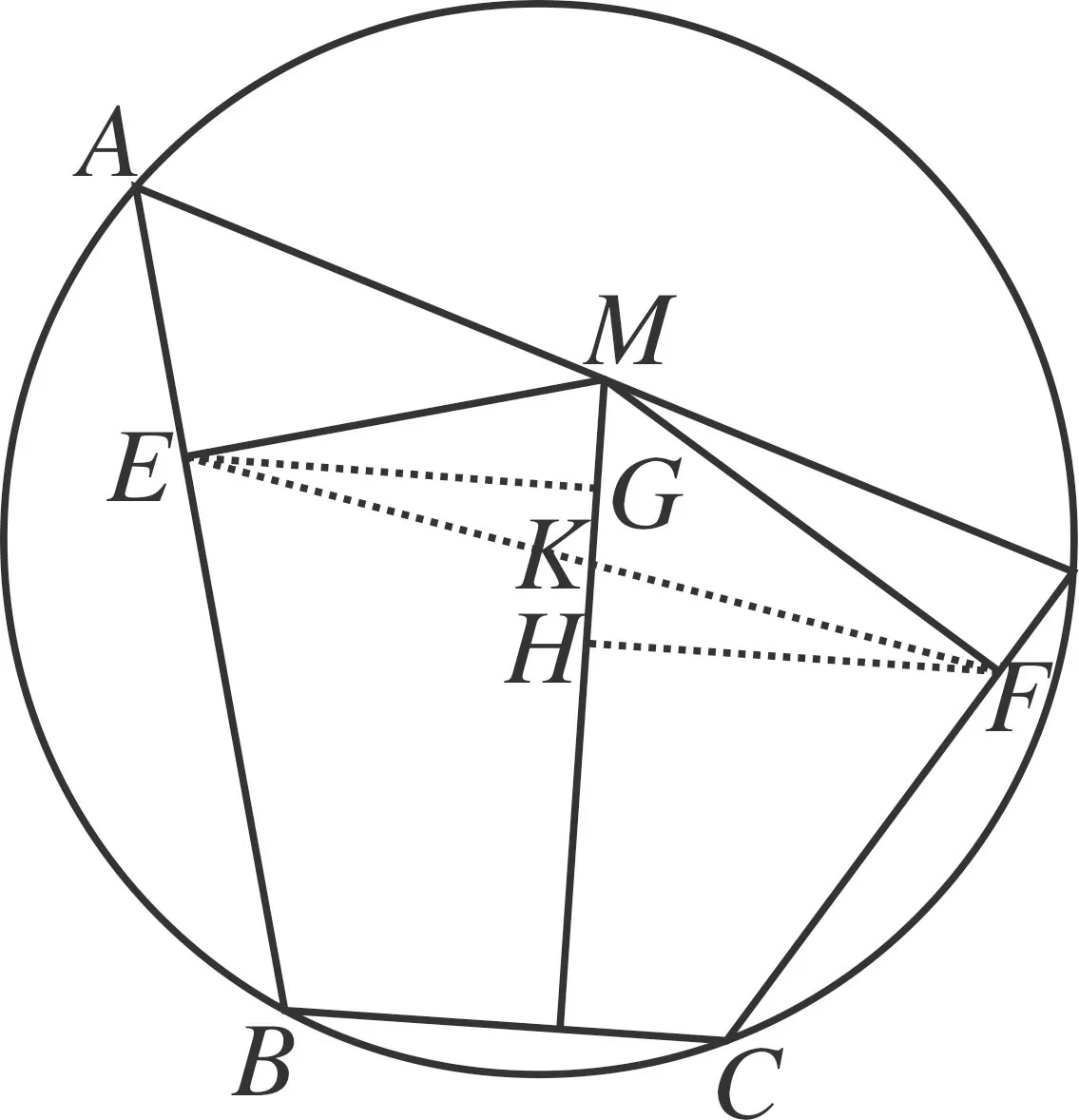
图4

如图4，过点E、F作MN的垂线，垂足分别设为G、H.

在Rt△EGM和Rt△MFD中，由∠EMG=∠D，得

△EGM∽△MFD.

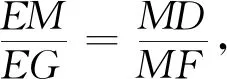
所以EG=FH.

从而△EGK≌△FHK，所以EK=KF.

思路2 证明中点即交点

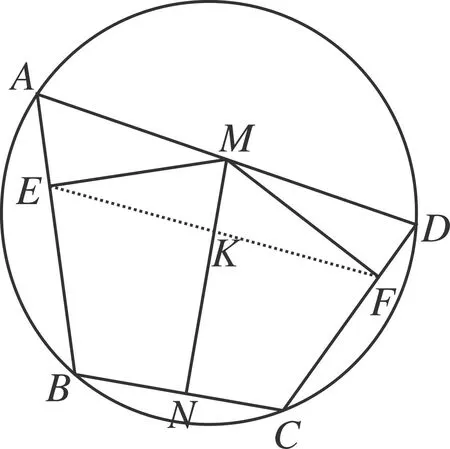
图5

如图5，连接EF，取EF的中点K，下证M、K、N共线即可.

解法四 (向量法)

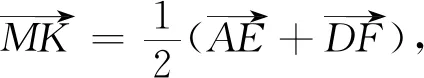
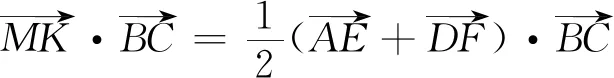
=0.

所以MK⊥BC.由于过一点有且仅有一条垂线，于是M、K、N共线.

解法五 (余弦定理)

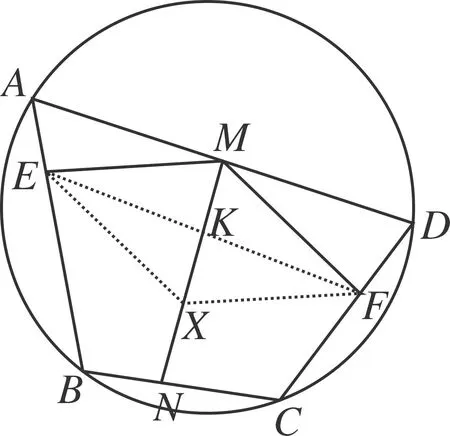
图6

如图6，倍长MK至X，连接XE、XF，

于是四边形XEMF为平行四边形，且∠EMF=180°-∠AME-∠DMF=∠A+∠D.

在△XEM中，MX2=EM2+EX2-2EM·EX·cos∠MEX=sin2A+sin2D+2sinA·sinD·cos(A+D).

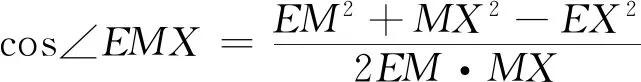
所以∠EMK=∠EMX=∠D=180°-∠B=∠EMN.于是M、K、N共线.

点评① 值得指出的是，两种思路本质区别是针对点K的生成方式不同，却都能达到证明目标；②由上可以看出，本题结构简洁，思路自然，解法多样.同时作为一道预赛试题，能较好地检测学生的能力水平，体现出深刻的思考价值.

3 相关探究

鉴于上述证法思路与具体过程，笔者对试题的原结构中的一些条件强化或者弱化，可以得出类似的相关结论，具体如下.

图7

命题1 如图7，AD是圆的直径，B、C是圆上的定点.自圆心M作MN⊥BC，ME⊥AB，MF⊥CD，N、E、F为垂足.则MN过线段EF的中点K.

点评①容易发现E、N、F分别是弦AB、BC、CD的中点，从而四边形MENF为平行四边形，于是EF、MN互相平分，所以结论成立；②上结论实质是原题的特殊状态，同时也是参考答案证明方法的核心.

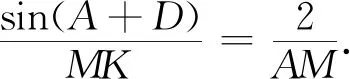
证明以点M为视点，注意到E、K、F三点共线.

注意到∠KMF=∠A,∠EMK=∠D，

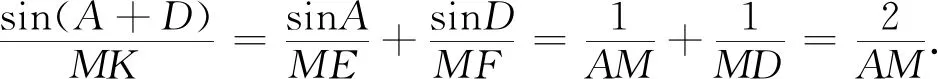
点评上结论揭示了MK,AM长度与角度A+D正弦之间定量的关系，同时也与解法四中由余弦定理得到MX=

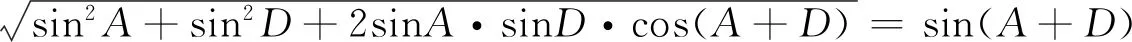
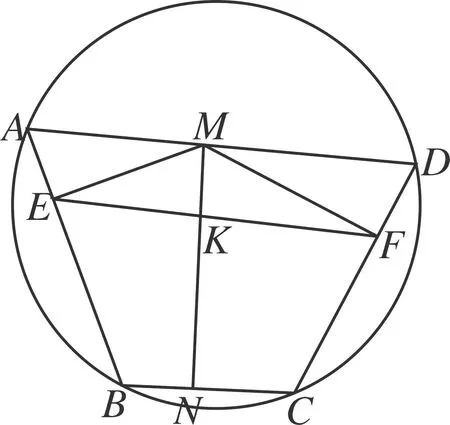
图8

命题3 如图8，圆内接四边形ABCD中，自边AD的一动点M，作MN⊥BC，ME⊥AB，MF⊥CD，N、E、F为垂足，EF与MN交于点K.则

点评在原结构中初步释放点M的位置(仍在AD上)，其它条件不变，那么点K为EF中点结论改成点K分线段EF所成的比与点M分线段AD所成的比相等.

图9

命题4 如图9，圆内接四边形ABCD中，自边AD的一动点M，作ME交AB于E，作MN交BC于M，作MF交CD于F，且∠MEB=∠MNC=∠MFD(注：这里的角为有向角，∠MEB表示EM旋转至EB角的大小)，EF与MN交于点K.设△AME和△MFD的外接圆半径分别为R1和R2.则

点评命题4表明了原构型中过点M作垂线的条件可以弱化成两组四点共圆而结论本质不变.

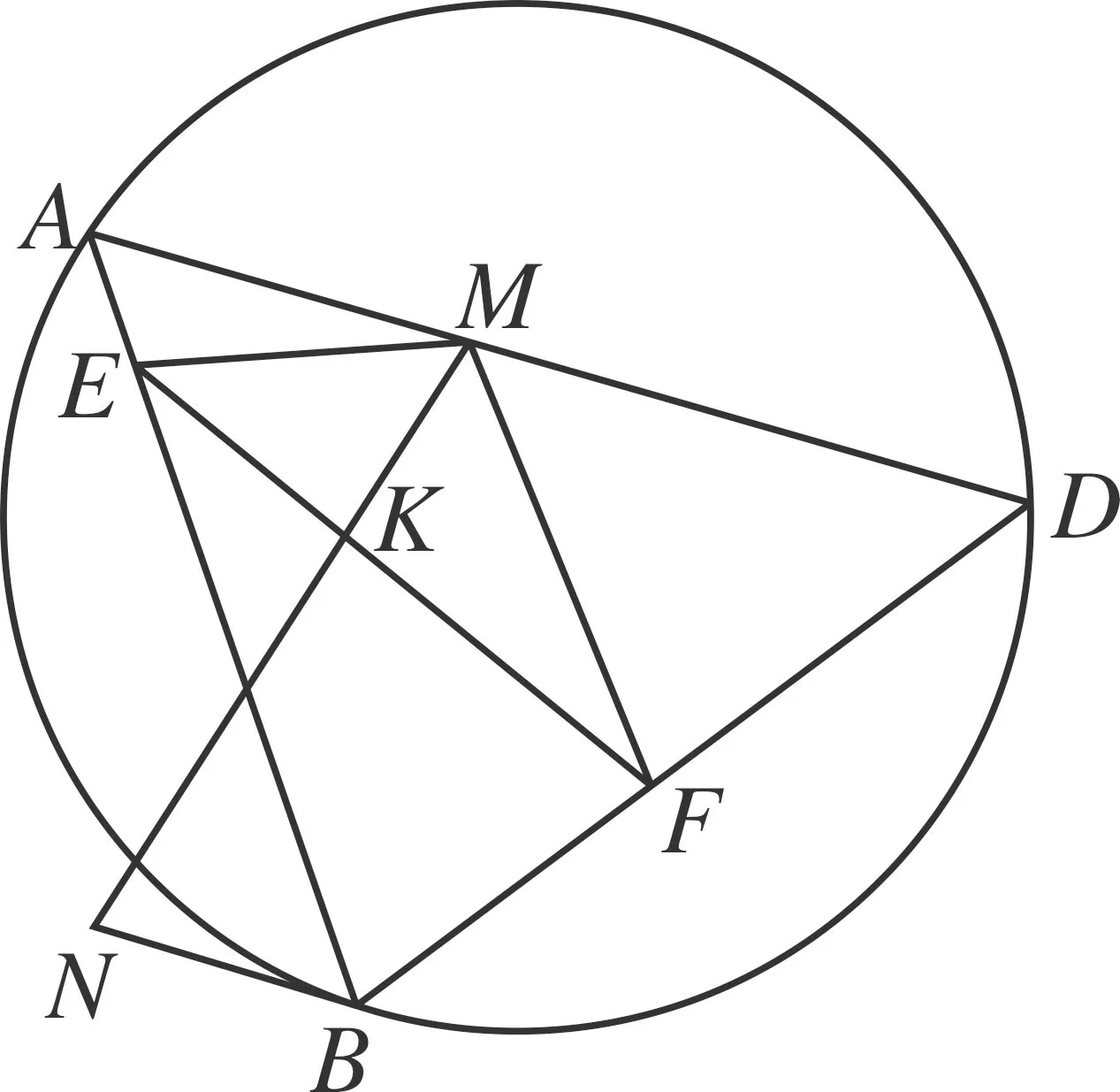
图10

命题5 如图10，圆内接△ABD中，自边AD的一动点M，作ME交AB于E，作MN交BC于M，作MF交BC于F，且∠MEB=∠MNC=∠MFD(注：此处为有向角)，EF与MN交于点K.设△AME和△MFD的外接圆半径分别为R1和R2.则

点评命题4中，当点B、C重合时，四边形ABCD退化成△ABD，边BC退化成切线BN，即可退化成命题5.

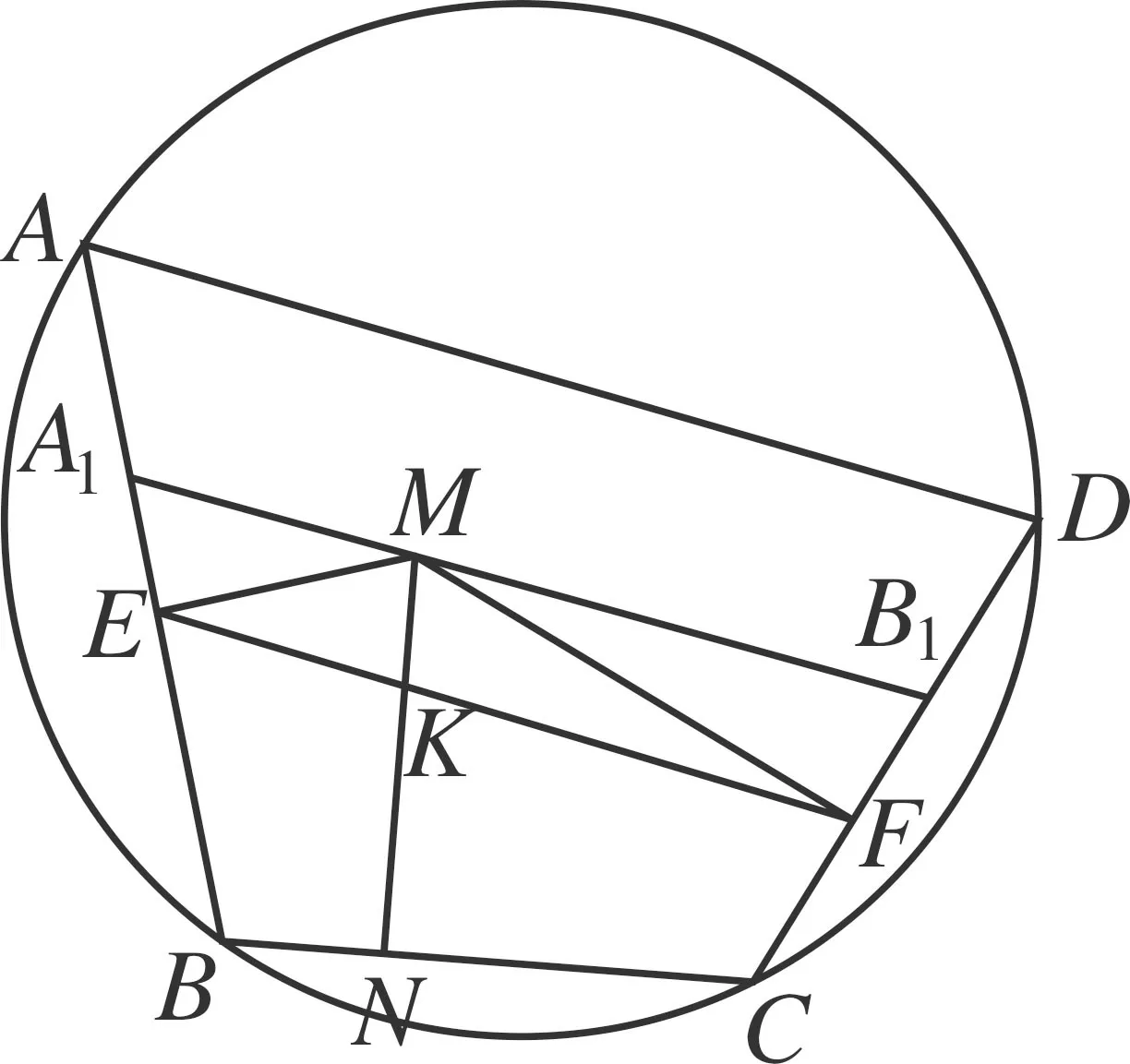
图11

命题6 如图11，圆内接四边形ABCD中，自一动点M，作ME交AB于E，作MN交BC于M，作MF交CD于F，且∠MEB=∠MNC=∠MFD(注：此处为有向角)，EF与MN交于点K，过M作AD平行线交直线AB、CD于A1、D1.设△A1ME和△MFD1的外接圆半径分别为R1和R2.则

点评命题6中彻底释放点M的位置(不一定在AD上)仍然有类似结论，证明可由A1、B1、C、D共圆再结合命题4立得.