维纳过程在数理金融学中的应用错误及纠正

● 高 宏

一、引言

维纳过程（Wiener process）是描述复杂随机现象的基本随机过程，在自然科学、工程技术和社会科学领域有着广泛的应用。随机过程一般使用随机变量和样本函数两种变量，分别从状态空间和时域两个维度进行描述，但是维纳过程的定义及性质却是单独以随机变量的形式从状态空间给出的，不能直接用来描述随机现象随时间演变的实际过程，在应用时往往会出现概念性错误。本文指出了数理金融学直接将维纳过程的随机变量模型和状态空间统计特性用于描述金融资产价格随时间演变过程的概念性错误，并根据金融资产价格与时间一一对应的函数关系，使用维纳过程样本函数来描述金融资产价格随时间演变的过程，建立了股票价格积分模型，推导出了股票价格的自相关函数和功率谱密度。

二、维纳过程定义

定义：设{W（t），t≥0}为随机过程，如果

（1）W（0）=0；

（2）ΔW（t）为服从N（0，σ2）的平稳独立增量；

（3）对任意的t＞s≥0，W（t）-W（s）～N（0，σ2（t-s））。

则称{W（t），t≥0}是参数为σ2的维纳过程，或布朗运动。

由维纳过程定义，维纳过程具有如下特性：

（1）W（t）服从（0，tσ2）正态分布；

（2）W（t）为马尔科夫过程；

（3）W（t）为鞅过程。

事实上，维纳过程 W（t）是定义在ΩT上的二元函数，对于固定的t∈T，W（t）是定义在状态空间Ω上的函数，称为随机变量，自变量为样本点ω；对于固定的ω∈Ω，W（t）是一个确定性的时间函数，通常称为样本函数或样本轨道，自变量为时间t。

维纳过程的定义是以随机变量形式从状态空间给出的，因此W（t）并不表示W是t的函数，它只表示t时刻随机变量W在样本空间Ω的状态。

为区别维纳过程的随机变量和样本函数，用大写字母W（t）表示随机变量，用小写字母w（t）表示样本函数。因此，维纳过程W（t）是一族样本函数w（t）的集合，所有样本函数在t时刻的取值构成了随机变量的定义域。

从维纳过程的定义可以看出，维纳过程为非平稳随机过程，不具备各态历经性，其随机变量W（t）的统计平均和样本函数w（t）的时间平均不相等。

三、应用错误

观察股票价格s随时间t的变化过程，有s和t两个变量，对于自变量t的每一个值，s都有唯一一个确定的值与它对应，因此，s是t的函数，可表示为s（t）。

设y（t）=ln s（t）为股票对数价格，则股票价格s（t）在Δt区间上的对数收益率为

显然，Δy（t）也是t的函数。

Osborne（1959）和 Fama（1965）的实证研究结果表明，股票价格对数收益率为均值为零的白噪声序列，与维纳过程样本函数w（t）的差分Δw（t）相同。但是，Osborne和Fama在建立股票价格数学模型y（t）时，使用的是维纳过程随机变量W（t）的差分ΔW（t），即

或

式（2）和式（3）左边的y（t）为时域样本函数，右边的W（t）为定义在状态空间的随机变量，完全没有等价关系。

若将维纳过程随机变量W（t）在状态空间的统计特性直接用于时间函数y（t），则会得出股票价格y（t）服从正态分布、股票价格为马尔科夫过程和鞅过程、股票价格的变化与时间的平方根成正比等一系列错误结论。

维纳过程的上述应用错误直接导致数理金融学产生了另外一个更为严重的错误。为了让式（2）和式（3）两边在形式上保持相等，Merton（2013）、Wilmott（2015）、Ross（2014）和Hull（2013）竟将股票价格与时间之间的数量关系假设为状态空间的随机变量，致使数理金融学的研究对象和研究方法发生了根本性变化，研究对象从时域的单个样本函数改变为状态空间所有样本函数的集合，研究方法从时域函数分析转变为状态空间概率分析，因此建立的随机数学模型和推导出的所有结论必然与事实不符，无法正确描述股票价格运动现象及规律，更不能预测股票价格的发展趋势和变化结果（Triana，2014）。

四、错误纠正

将式（3）中的维纳过程随机变量W（t）替换为样本函数w（t），有

由维纳过程定义，dW（t）为高斯白噪声过程，因此式（4）可改写为

式中ε（t）为服从N（0，σ2）正态分布的高斯白噪声样本函数。

（一）股票价格数学模型

对式（5）的微分数学模型进行积分，可得股票价格的积分模型

显然，股票价格y（t）是对ε（t）的变限积分，表明式（6）为非线性时变模型。

在实际应用时，可以放宽白噪声ε（t）服从正态分布的要求，只需白噪声样本函数ε（t）在不同时刻的取值互不相关，即

式中Rε（τ）为ε（t）的时间自相关函数，N0为正实常数，δ（t）为单位冲击函数。N0的物理意义代表白噪声信号在单位电阻上产生的平均功率。

（二）股票价格自相关函数

股票价格y（t）的时间自相关函数为

式中，为时间间隔。

（三）股票价格功率谱密度

在［0，t］区间，y（t）的平均功率有限，自相关函数Ry（）绝对可积，根据维纳-辛钦定理，y（t）的功率谱密度Sy（ω）是其自相关函数Ry（τ）的傅立叶变换，有

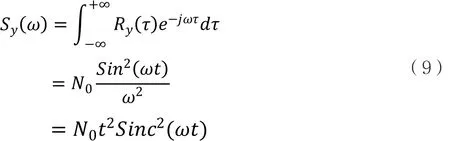
式中，Sinc（ωt）为辛格函数，是正弦函数Sin（ωt）与单调递减函数1/ ωt的乘积。

从式（9）可以看出，股票价格的功率谱密度与频率的平方成反比。Andreadis（2000）对1988年12月1日至1998年4月1日的S&P 500标准普尔指数（日）进行了功率谱计算，实证结果显示：S&P 500指数的对数功率谱密度与频率的平方成反比，因此式（9）得到实验验证，表明式（6）的积分数学模型、式（8）的自相关函数和式（9）的功率谱密度均被证实。

Sy（ω）在ω=0处有最大值N0t2，在时域中就表现为，股票价格y（t）中存在一条与时间t成正比的线性趋势线，y（t）围绕趋势线上下波动，与实际股票对数价格中存在长期线性趋势这一观察现象完全相符。

五、结论

本文指出了数理金融学使用维纳过程刻画金融资产价格随时间演变过程时的概念性错误，并根据金融资产价格与时间一一对应的函数关系，使用维纳过程样本函数来描述资产价格随时间演变的过程，建立了股票价格积分模型，推导出了可揭示金融资产价格运动规律的自相关函数和功率谱密度，从理论上证明了股票价格具有可预测性，得出了股票价格的波动幅度与波动频率成反比的运动规律，可为证券投资活动的价格分析、价格预测及风险管理提供有效的数学模型及分析工具。